2015-02-22
Elektrony i dziury
•
•
•
•
•
struktura pasmowa
podział ciał stałych
masa efektywna nośników
pojęcie dziury
półprzewodniki
Co to jest teoria pasmowa
Teoria pasmowa jest kwantowo-mechanicznym opisem
zachowania elektronów w krystalicznym ciele stałym.
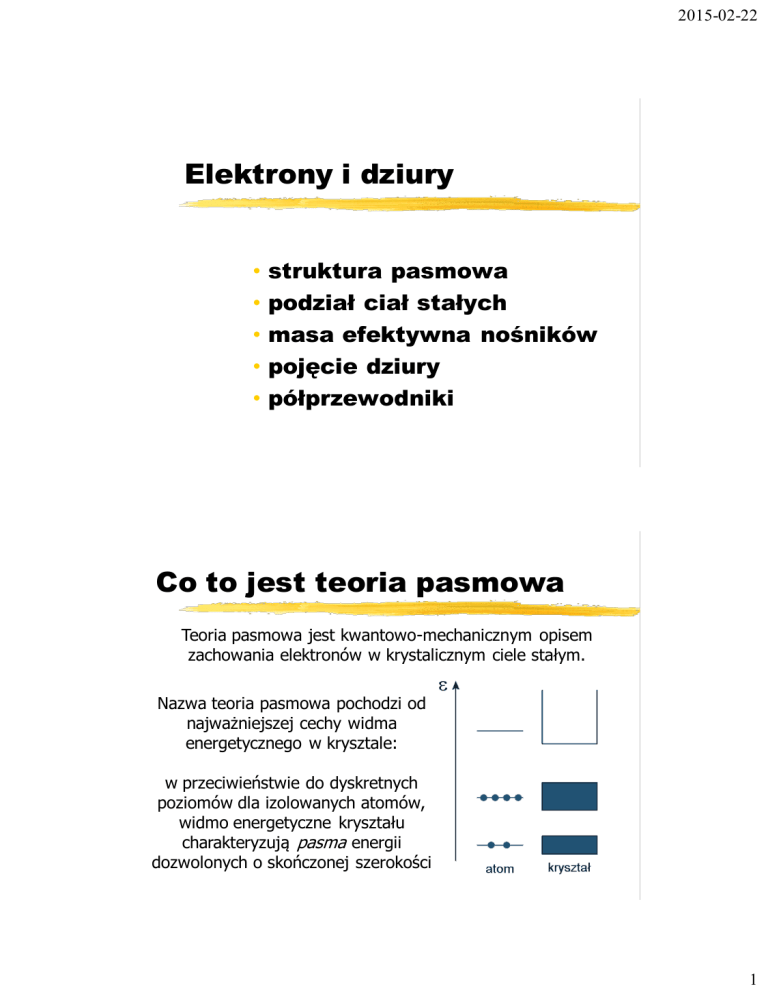
Nazwa teoria pasmowa pochodzi od
najważniejszej cechy widma
energetycznego w krysztale:
w przeciwieństwie do dyskretnych
poziomów dla izolowanych atomów,
widmo energetyczne kryształu
charakteryzują pasma energii
dozwolonych o skończonej szerokości
1
2015-02-22
Wady modelu elektronów
swobodnych
E
przyjęcie stałego potencjału
w modelu elektronów swobodnych
nie uwzględnia dyskretnej struktury
krystalicznej ciał stałych
istotny wpływ na zachowanie
elektronów odgrywa ich
oddziaływanie z jonami sieci
brak również uwzględnienia
0
oddziaływania elektronów pomiędzy sobą
oba typy oddziaływań można rozdzielić stosując
różne rodzaje przybliżeń: jednoelektronowe,
elektronów prawie swobodnych lub silnie
związanych
x
jako punkt wyjścia przyjmujemy
funkcje falowe i zdegenerowane
poziomy energetyczne
pojedynczych atomów
w wyniku zbliżania atomów
następuje rozszczepienie
poziomów w pasma i ewentualne
przekrywanie (zlewanie)
szerokość pasma zależy od
przekrywania odpowiednich
funkcji falowych
głęboko leżące poziomy są
nieznacznie poszerzone i
zachowują swój atomowy
charakter
energia elektronu E
Powstawanie pasm
2p
2s
1s
r0
odległość r
2
2015-02-22
Izolowane, swobodne atomy Na
w atomie swobodnym (a)
każdy poziom jest 2(2l+1)
krotnie zdegenerowany
dla N atomów liczba
podpoziomów wynosi
2N(2l+1)
0
bariera potencjału nie
zezwala elektronom
swobodnie poruszać się
między atomami
elektrony są zlokalizowane,
funkcje falowe nie
zachodzą na siebie
3s
2s
Na
Na
Poziom zerowy
+
3s1
+
1
3s
2p6
6
2p
2s2
1s
1s
2
2s
2
2
1s
r >> a
U
U
Zmiana stanu elektronów
przy zbliżaniu się atomów
Przy odległościach równych stałej sieci 0,43 nm otrzymujemy:
(b)
obniżenie poziomu potencjału
poniżej stanu 3s
elektrony 3s stają się
swobodne
0 +
funkcje falowe tych
elektronów zachodzą na siebie
funkcje falowe elektronów
wewnętrznych nie ulegają
zmianie
pojedyncze poziomy ulegają
Na
rozszczepieniu tworząc pasmo
3s
2s
1s
+
+
+
3s
2p
2s
1s
Na
Na
Na
o
a = 4.3A
3
2015-02-22
Zapełnianie pasm przez
elektrony
Pod względem charakteru zapełnienia pasm przez elektrony
możemy podzielić wszystkie ciała na trzy grupy:
izolatory i półprzewodniki - niższe pasma
całkowicie zapełnione, wyższe poczynając od
pewnego, całkowicie puste
metale proste - nad całkowicie zapełnionymi
pasmami istnieje pasmo zapełnione częściowo
metale z pasmami nakładającymi się najwyższe całkowicie zapełnione pasmo,
zachodzi na położone nad nim najniższe
E
pasmo puste, wtedy oba zapełniają się
częściowo
k
Podział ciał stałych
O własnościach fizycznych ciał stałych decydują:
E
kształt i sposób obsadzenia elektronami dwóch najważniejszych
pasm energetycznych
pasma przewodnictwa - najniższego pasma nie
zapełnionego
pasma podstawowego (walencyjnego) - najwyższego
pasma obsadzonego przez elektrony
odległość między tymi pasmami E g - zwana przerwą
energetyczną (pasmem zabronionym)
izolatory Eg > 3 eV - nie przewodzą prądu
półprzewodniki Eg < 3 eV, choć GaN ( 3,4 eV)
diament (5,4 eV)
metale Eg = 0 - pasma zachodzą na siebie
ta sama substancja może mieć w pewnych warunkach bądź
właściwości półprzewodnikowe, bądź metaliczne
4
2015-02-22
Masa efektywna elektronu
Masa efektywna jest charakterystyką rozważanego pasma a
nie elektronu
pojęcie masy efektywnej ma znaczenie fizyczne, gdyż wyraża
wpływ periodycznego potencjału sieci na dynamikę elektronu
m* opisuje ruch elektronu pod wpływem sił zewnętrznych F
siły wewnętrzne wywierane przez sieć jako wynik
oddziaływania elektronu z potencjałem krystalicznym są
uwzględnione w wartości m* różnej od masy rzeczywistej m0
a
F
m*
m0 a m0
F
F Fsiec
m*
m* m0
wartość m* jest z reguły mniejsza od m0
F
F Fsiec
2
E
m* 2
dk
2 d
1
Pasma paraboliczne
E
Dla pasm parabolicznych zachowanie
pojedynczego elektronu w paśmie
przewodnictwa opisuje się stałą masą m*e
Ec
-q
d 2E
E (k ) E c 2
k 2 ...
dk
k 0
2 k 2
E (k ) E c
2me
2k 2
2me
Ev
2k 2
2me
Ec
przejście
proste
Ev
Podobnie będzie z elektronami w
paśmie walencyjnym, gdzie m*e < 0
jest masą efektywną tych elektronów
E(k ) Ev
2k 2
Ev
-ke
0
ke
2k 2
2mhe
k
2 me
5
2015-02-22
Odwrotne zjawisko
termoelektryczne
W metalach w których pasmo
walencyjne jest prawie całkowicie
zapełnione występuje odwrotne
zjawisko termoelektryczne - jakby
dziury (ładunki dodatnie) dyfundowały
od gorącego do zimnego końca
metal prosty
T1
>
T2
półmetal
E
cynk Zn
kadm Cd
bizmut Bi
ujemna m*
k
Pojęcie dziury
W przypadku pasma prawie całkowicie zapełnionego zamiast o
ruchu brakującego elektronu o ujemnej masie wygodniej jest
wprowadzić pojęcie dziury h (hole) o dodatnim ładunku +e i vh
= vb.el
Właściwości
dziury:
im większa jest energia nieobsadzonego
przez elektron stanu w paśmie walencyjnym
tym mniejsza jest energia dziury
qh e
kh kb.el
v h v b.el
mh
k
me
Eel
masa efektywna dziury jest
równy masie wzbudzonego
elektronu i ma znak przeciwny,
czyli jest dodatnia
k
dziura
k
pusty stan
ke
kh
b.el
k
Eh
6
2015-02-22
Półprzewodniki
Półprzewodniki to materiały o przerwie energetycznej poniżej
3 eV, które w temperaturze 0 K mają całkowicie zapełnione
pasmo walencyjne i puste pasmo przewodnictwa
w wyższych temperaturach pod wpływem wzbudzeń
termicznych, część elektronów z pasma walencyjnego
przechodzi do pasma przewodnictwa
swobodne elektrony w p.p. i dziury w p.w. decydują o
przewodnictwie elektrycznym półprzewodnika
konduktywność materiałów półprzewodnikowych zmienia się
w przedziale od 10–8 do 106 (Wcm)–1
Stan równowagi
EFn + EFp = –Eg
W ogólnym przypadku poziomy Fermiego dla elektronów i dziur
mogą się nie pokrywać.
n Nc eE kT
E
Fn
Ec
0
EFp
Eg
Ec
EFn = EF
EFn
EFp
EFn
Ev
0’
E’
generacja
Ec
EFp
Ev
p Nv e
Ev
EFp kT
równowaga
rekombinacja
W stanie równowagi poziomy Fermiego pokrywają się
7
2015-02-22
Półprzewodniki samoistne
Wpływ domieszek na właściwości fizyczne jest
zaniedbywalny
charakteryzują się doskonałą strukturą
krystaliczną, bez obcych atomów i defektów
strukturalnych
swobodne nośniki powstają tylko kosztem
rozerwania wiązań kowalencyjnych
liczba dziur jest równa liczbie swobodnych
elektronów i nazywa koncentracją samoistną
n p ni
Statystyka nośników w p.s.
n p ni
ni2 np Nc eEFn
ni
Nc Nv e
kT
Nv e
EFp kT
E g 2kT
Nc Nv e
ni
EFn EFp kT N N eEg
c v
22kT
h3
32
kT
m m
e
3 4 E g 2kT
e
h
Koncentracja równowagowa w półprzewodniku samoistnym określona
jest przez szerokość pasma zabronionego i temperaturę półprzewodnika
Półprzewodnik
Si
Ge
Sn
Eg (eV)
1,12
0,67
0,08
ni (m-3)
2·1016
3·1019
1·1024
T (K)
100
300
600
ni (m-3)
3·107
3·1019
6·1023
8
2015-02-22
Położenie poziomu Fermiego
EF
Eg
2
3
m
kT ln h
4
me
E
Ec
EF
mh me
mh me
mh me
Ev
Dla większości samoistnych
półprzewodników w
temperaturach pokojowych
przesunięcie poziomu
Fermiego można zaniedbać,
czyli EF = –Eg/2
T
Półprzewodniki samoistne
i domieszkowe
półprzewodniki typu n
przewodnictwo elektronowe
domieszki donorowe: P, As, Sb
V grupa układu okresowego
półprzewodniki typu p
przewodnictwo dziurowe
domieszki akceptorowe: B, Ga, In
III grupa układu okresowego
9
2015-02-22
Położenie poziomu Fermiego
0
niskie
temp.
wyczerpanie
domieszki
przewodnictwo
samoistne
Ev
Zależność koncentracji
elektronów od temperatury
12
Dla T < Ts
Dla T > Ti
1
n Nd Nc e E d
2
ni Nc Nv 1 2 e
2 kT
Eg 2kT
n Nd
10
2015-02-22
Dla typu p
E
½Eg
g
Ea
kT
EF
12
1
p NaNv
2
Dla T < Ts
Dla Ts < T < Ti
np ni2
n
p
p Na n
Na ~ ni
Dla T > Ti
e
Ea 2kT
n
ni >> Nd
ni Nc Nv 1 2 e
ni2
p
Na Na2 4ni2
2
Na Na2 4ni2
2
n p ni
Eg 2kT
Ruchliwość nośników
ruchliwość nośników to średnia prędkość unoszenia (dryftu) przy
jednostkowym natężeniu zewnętrznego pola elektrycznego = vd/E
ustalona wartość ruchliwości jest wynikiem zderzeń nośników z
fononami i domieszkami sieci
średnia prędkość dryftu zależy od natężenia pola elektrycznego i czasu
pomiędzy zderzeniami (czas relaksacji zderzeniowej )
vd
eE
me
v
e
e d
E
me
ruchliwość nie zależy od czynników zewnętrznych a jedynie od
właściwości ciała stałego
11
2015-02-22
Zależność ruchliwości od
temperatury
Rozpraszanie
na domieszkach
Ruchliwość
w niskich temperaturach przeważa
rozpraszanie na domieszkach
~ T3 2
w wyższych temperaturach
ruchliwość maleje w wyniku
wzrostu rozpraszania na
drganiach akustycznych sieci
~ T 3 2
ze wzrostem koncentracji domieszki
ruchliwość nośników maleje
ruchliwość elektronów jest
zazwyczaj większa od ruchliwości
dziur
T=300K
Si
~T
Rozpraszanie
na fononach
Nd
,
Nd>Nd
3/2
~T-3/2
Temperatura
Ge
InSb
InAs
PbS
h (m2/Vs)
0,060
0,190
0,075
0,046
0,060
e (m2/Vs)
0,150
0,390
7,700
3,300
0,055
Przewodnictwo
półprzewodników
prędkość dryftu określa gęstość prądu
e2
j envd nE
me
porównując z
prawem Ohma
j E
e
e 2 n
me
e
me
e ene
h ep h
w półprzewodnikach transport ładunku jest spowodowany zarówno
elektronami, jak i dziurami, konduktywność wyraża się wzorem:
e ne p h
12
2015-02-22
Masa efektywna,
a krzywizna pasm
W krzemie powierzchnie izoenergetyczne w p.c. są
elipsoidami obrotowymi więc występują dwie
masy podłużna ml i poprzeczna mt
W GaAs p.c. jest sferyczne – tylko jedna masa
d 2E
m* 2 2
dk
E
me*
elektrony
Struktura maksimum pasma walencyjnego p.v. jest
bardziej skomplikowana: poza dwoma pasmami o
różnej krzywiźnie istnieje trzecie pasmo oddalone
o energię w wyniku oddziaływań spin-orbita
Elektron
Eg
Dziura
ml
mt
mhh
mhl
mhso
Si
0,98
0,19
0,49
0,16
0,38
GaAs
0,07
-
0,68
0,12
0,20
me* mh*
1
*
dziury mhl
lekkie
k
dziury
ciężkie
*
mhh
*
dziury odszczepione
mhso
13