Prawo Ohma

Prawo Ohma
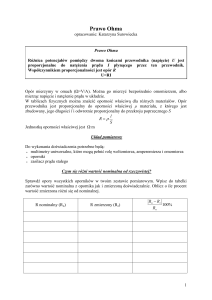
Prawo Ohma opisuje sytuację, najprostszego
przypadku związku między napięciem
przyłożonym do przewodnika (opornika), a
natężeniem prądu przez ten przewodnik
płynącego.
Sformułowanie prawa Ohma
Stosunek natężenia prądu płynącego przez przewodnik do napięcia pomiędzy jego końcami
jest stały.
Wzór na prawo Ohma - postać 1
I - natężenie prądu (w układzie SI w amperach – A)
U - napięcie między końcami przewodnika (w układzie SI w woltach – V)
Wzór na prawo Ohma - postać 2
Inaczej prawo Ohma można sformułować także w postaci zapisu symbolicznego:
I ~ U (I jest proporcjonalne do U)
Natężenie prądu płynącego przez przewodnik jest proporcjonalne do przyłożonego napięcia.
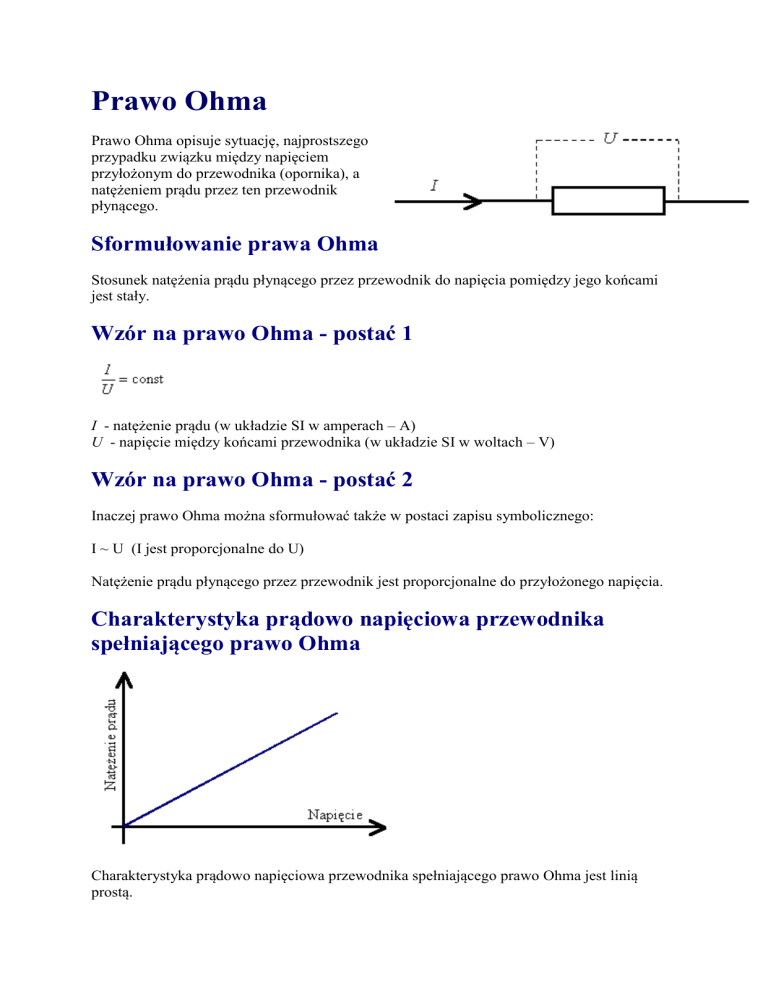
Charakterystyka prądowo napięciowa przewodnika
spełniającego prawo Ohma
Charakterystyka prądowo napięciowa przewodnika spełniającego prawo Ohma jest linią
prostą.
Interpretacja prawa Ohma
Prawo Ohma mówi nam, że natężenie płynącego przez przewodnik prądu dokładnie „nadąża”
za zmianami napięcia. Gdy napięcie wzrasta 2-krotnie, wtedy wywołany tym napięciem
przepływ prądu też osiągnie natężenie 2 razy większe, gdy napięcie wzrośnie 5 krotnie, to
natężenie prądu też powinno wzrosnąć 5 razy w stosunku do wartości początkowej.
Jeszcze inaczej mówiąc:
Natężenie prądu, będące efektem przyłożonego napięcia, zachowuje się proporcjonalnie do
swojej przyczyny.
Prawo Ohma jest spełniane przez część materiałów – głównie przez metale i materiały
ceramiczne. Jest jednak dużo substancji które prawa Ohma nie spełniają, czyli natężenie
przepływającego przez nie prądu zmienia się w sposób nieproporcjonalny do napięcia.
Kiedy prawo Ohma jest spełnione?
Prawo Ohma jest prawem materiałowym (nie uniwersalnym), co oznacza, że sprawdza się
tylko dla niektórych materiałów - substancji. Poza tym prawo to jest słuszne tylko w
określonych napięć i przy ustalonych warunkach zewnętrznych (np. stała powinna być
temperatura).
Prawo Ohma jest spełniane głównie przez metale i materiały ceramiczne. Jest jednak dużo
substancji, które prawa Ohma nie spełniają, czyli natężenie przepływającego przez nie prądu
zmienia się w sposób nieproporcjonalny do napięcia. Poza tym stosowalność prawa Ohma
może istotnie zależeć od zakresu napięć - np. w typowych sytuacjach przy małych napięciach
natężenie jest proporcjonalne do napięcia, ale po przejściu w zakres dużych napięć,
proporcjonalność się załamuje. Na rysunku poniżej przedstawione są charakterystyki
materiałów, które nie spełniają prawa Ohma.
Rysunek - przykład charakterystyk materiałów NIE spełniających prawa Ohma.
Materiały spełniające i nie spełniające prawa Ohma
Do materiałów spełniających prawo Ohma należą przewodniki:
metale (np. miedź, złoto, srebro, żelazo)
grafit
niektóre materiały ceramiczne
większość elektrolitów
Nie spełniają prawa Ohma:
półprzewodniki
gazy (choć w pewnych zakresach napięć mogą być one zgodne z tym prawem).
I prawo Kirchhoffa
Wprowadzenie
I prawo Kirchhoffa odnosi się do sytuacji gdy prąd płynący w jakimś układzie ulega
rozgałęzieniu, czyli gdy przewody z prądem łączą się w jakimś punkcie..
Ponieważ ładunki elektryczne nie mogą znikać, ani powstawać z niczego, a standardowy
przewodnik właściwie nie potrafi ich gromadzić (wyjątkiem są kondensatory), to jasne jest,
że:
Jeśli w jakimś czasie do rozgałęzienia dopłynął ładunek q, to w tym samym czasie z tego
rozgałęzienia musiał również taki sam ładunek q odpłynąć.
Ponieważ jednak ładunek wpływający, czy wypływający w jednostce czasu to nic innego jak
natężenie prądu I, więc prawo to można sformułować odwołując się do tego pojęcia natężenia
prądu:
Sformułowanie I prawa Kirchhoffa
Suma natężeń prądów wpływających do rozgałęzienia, równa jest sumie natężeń prądów
wypływających z tego rozgałęzienia.
Powyższe prawo można zapisać wzorem:
Iwpływające1 + Iwpływające2 + Iwpływające3 + ... = Iwypływające1 + Iwypływające2 + Iwypływające3 + ...
Bardziej zwięzły wzór można otrzymać dzięki posłużeniu się znakiem sumowania – sigma Σ.
Tutaj np. Σ Iwpływające oznacza sumę natężeń wszystkich prądów wpływających.
Σ Iwpływające = Σ Iwypływające
Przykład 1
Prądy wpływające do rozgałęzienia (należy zwrócić uwagę na zwroty strzałek)
Σ Iwpływające = 2A + 3A + 5A = 10A
Σ Iwypływające = 7A + 3 A
ΣIwpływające = Σ Iwypływające
Przykład 2
Dla sytuacji na rysunku:
I1 + I2 + I3 = I4 + I5 + I6
Bo z zaznaczeń strzałkami wynika, że prądy I1, I2, I3 wpływają do rozgałęzienia, a prądy I4,
I5, I6 z niego wypływają.
Opór elektryczny i
przewodnictwo
elektryczne
Prawa Ohma głosi, że:
stosunek natężenia prądu płynącego przez przewodnik do napięcia pomiędzy jego końcami jest stały.
Wartość tego stosunku jest nazywana jest przewodnictwem elektrycznym:
G - przewodnictwo elektryczne (w simensach S)
I - natężenie prądu (w układzie SI w amperach – A)
U - napięcie między końcami przewodnika (w układzie SI w woltach – V)
Jednostką przewodnictwa w układzie SI jest simens - S:
1 S = 1/ Ω = A/V.
Opór przewodnika
Z kolei odwrotność przewodnictwa, czyli stosunek napięcia do natężenia prądu jest określany mianem oporu
elektrycznego. Jest on oznaczany literą R (bo inne jego określenie to rezystancja).
W takim układzie „wzór na prawo Ohma” (przypominam, że sam wzór nie wyraża jeszcze prawidłowo tego
prawa) ma postać:
R - opór elektryczny (w omach - Ω )
I - natężenie prądu (w układzie SI w amperach – A)
U - napięcie między końcami przewodnika (w układzie SI w woltach – V)
Jednostką oporu jest 1 om. Om oznaczany jest grecką literą „duże omega” – Ω.
[R] = Ω = V/A
Opór elektryczny a prawidłowo sformułowane prawo Ohma
Prawidłowo sformułowane prawo Ohma wykorzystujące pojęcie oporu miałoby postać, że opór przewodnika
jest stały (opór ten nie zmienia się mimo zmian przyłożonego napięcia), co sprawdza się tylko w odniesieniu
do części materiałów.
Mamy więc:
Dla przewodników spełniających prawo Ohma opór elektryczny jest stały.
R = const
I to jest kolejna postać, w jakiej można formułować prawo Ohma.
Łączenie oporników
Najprostszym zastosowaniem prawa Kirchhoffa są reguły łączenia oporników. Najogólniej
możemy problem postawić tak: zmontowaliśmy pewien układ oporników, do którego z
zewnątrz dołączone jest pewne żródło (rys. 5.21). Chcemy cały układ zastąpić jednym
opornikiem. Pytamy więc: jaki jest opór zastępczy takiego układu. W tym skrypcie
ograniczymy się tylko do dwóch najprostszych przykładów.
Rysunek 5.21: Jaki jest opór zastępczy takiego układu
oporników?
Połączenie szeregowe dwóch oporników
Rozważmy prosty obwód, złożony ze żródła siły elektromotorycznej i dwóch oporników,
połączonych szeregowo (rys. 5.22). W tym przypadku:
Rysunek 5.22: Dwa oporniki połączone szeregowo


przez cały układ i przez każdy z oporników płynie prąd o takim samym natężeniu
całkowity spadek potencjału ( ) jest sumą spadków na poszczególnych oporach
(odpowiednio
i
;
):
(5.57)
Dzieląc 5.57 przez
i zauważając, że
, dostajemy:
(5.58)
czyli
(5.59)
Opór zastępczy
i
dwóch oporników połączonych szeregowo jest sumą ich oporów, czyli
.
Połączenie równoległe dwóch oporników
Rozważmy teraz obwód, złożony ze żródła siły elektromotorycznej i dwóch oporników,
połączonych równolegle (rys. 5.23). W tym przypadku:
Rysunek 5.23: Dwa oporniki połączone równolegle


do całego układu dołączone zostało napięcie
i to samo napięcie przyłożone jest do
każdego z oporników;
Natężenie prądu płynącego przez układ ( ) jest sumą natężeń płynących przez
poszczególne oporniki (odpowiednio
i
):
(5.60)
Dzieląc 5.60 przez
i zauważając, że
, dostajemy:
(5.61)
czyli
(5.62)
Odwrotność oporu zastępczego
dwóch oporników połączonych równolegle jest sumą
odwrotności ich oporów, czyli
i
.
Ze wzoru 5.62 możemy także wprost wyrazić
. Dodajemy ułamki po prawej stronie wzoru
(5.63)
i odwracamy wynik
Amper – jednostka natężenia prądu elektrycznego, jednostka podstawowa układu SI i
MKSA, oznaczana A.
Definicja 1 A - prąd o natężeniu 1 A jest to stały prąd elektryczny, który płynąc w dwóch
równoległych, prostoliniowych, nieskończenie długich przewodach o znikomo małym
przekroju kołowym, umieszczonych w próżni w odległości 1 m od siebie, spowodowałby
wzajemne oddziaływanie przewodów na siebie z siłą równą 2*10 -7 N na każdy metr długości
przewodu.
Do definicyjnego wyznaczenia jednostki służy waga prądowa. Dokładnością ustępuje jednak
kalibratorom prądu i w praktyce jest przez nie wyparta.
W układzie miar CGS odpowiednikiem ampera jest biot (Bi).
1 biot = 10 amperów
Jeśli przepływający przez dany przekrój prąd ma natężenie 1 A, oznacza to, że w ciągu 1 s
przepływa 1 C ładunku, czyli:
Nazwa amper pochodzi od nazwiska francuskiego fizyka André Marie Ampère'a.
Przedrostki SI [edytuj]
Wielokrotności i podkrotności jednostki (wyróżniono najczęściej używane):
Wielokrotności
Mnożnik Nazwa
100
amper
Podkrotności
Symbol Mnożnik
A
Nazwa
Symbol
101
dekaamper
daA
10–1
decyamper
dA
102
hektoamper
hA
10–2
centyamper
cA
kA
–3
miliamper
mA
–6
3
10
10
10
kiloamper
megaamper
MA
10
mikroamper
µA
109
gigaamper
GA
10–9
nanoamper
nA
–12
6
10
12
teraamper
TA
10
pikoamper
pA
1015
petaamper
PA
10–15
femtoamper
fA
–18
10
18
eksaamper
EA
10
attoamper
aA
1021
zettaamper
ZA
10–21
zeptoamper
zA
YA
–24
joktoamper
yA
24
10
jottaamper
Zobacz też [edytuj]
10
II prawo Kichhoffa
Drugie prawo Kirchhoffa jest uzupełnieniem pierwszego prawa
Kirchhoffa. Oba te prawa łącznie pozwalają na tzw.
„Rozwiązywanie obwodów”, czyli na obliczaniu natężeń prądów
płynących w różnych gałęziach obwodu, dzięki znajomości
oporów i sił elektromotorycznych źródeł.
II prawo Kirchhoffa odnosi się do spadków napięć na
elementach obwodu. Wynika ono ze zrozumienia faktu, że
napięcia w obwodzie nie biorą się znikąd. Jeżeli gdzieś na
oporniku jest jakieś napięcie, to znaczy, że musi też gdzieś istnieć źródło które wywołało prąd
przepływający przez opornik. I wszystkie napięcia pochodzące od źródeł muszą sumować się
z napięciami odkładającymi się na opornikach.
Pierwsze sformułowanie II prawa Kirchhoffa
II prawo Kirchhoffa można sformułować na kilka sposobów. Oto pierwszy z nich:
W obwodzie zamkniętym suma spadków napięć na wszystkich
odbiornikach prądu musi być równa sumie napięć na źródłach napięcia.
Przykład 1
Na rysunku podłączono woltomierze do źródła prądu oraz dwóch oporników – odbiorników
prądu. Jaki związek zachodzi między napięciami przez nie wskazywanymi?
Ten przykład jest prosty, bo mamy tu tylko jedno źródło prądu.
Jeśli napięcie na źródle oznaczymy UE , a napięcia na opornikach odpowiednio U1 i U2 , to
prawdziwy będzie związek:
UE = U1 + U2
Czyli np.
UE = 6 V
U1 = 4 V
U2 = 2 V
Lub
UE = 6 V
U1 = 1 V
U2 = 5 V