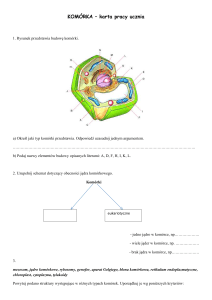
Funkcje matematyczne:
1.
Funkcje sumowania:
1.1. suma należy do funkcji o nieograniczonej liczbie parametrów. Parametrem może być
pojedyncza komórka lub dowolny zakres komórek<
=SUMA(A1:C1)
=SUMA(D1:D5)
=SUMA(A1:C5)
1.2.
1.3. suma kwadratów:
Oblicz sumę z
następującymi
parametrami:
=SUMA(A1:A5;B3;B4
:B5)
wartość sumy umieść
w komórce F2
=SUMA.KWADRATÓW(D11:D15)
5)
Ćwiczenie sprawdzające:
1. użyj formuły komórce E11: =D11 enter
2. w komórce E12 użyj formuły: =D12
3. zaznacz komórki (E11:E12) i kopiuj ich
zawartość do komórki E15.
4. w komórce F11 użyj formuły: =D11*E11
a następnie przez przeciąganie skopiuj ją do
komórki F15 W komórce F16 użyj for. sumy
1.4. suma jeżeli,
Sumowanie wybranych liczb według kryterium pozwala wykonać funkcja oparta na formule:
=SUMA.JEŻELI
suma ta posiada następujące argumenty: zakres, kryterium,
suma_zakres.
Zakres
obszar komórek na bazie których spełnione zostanie założenie formuły.
Kryterium
warunek jaki powinny spełniać elementy podanego zakresu.
Suma_zakres
zakres komórek, które mają być sumowane, jeżeli odpowiadające im
komórki z zakresu spełniają podany warunek.
1.5. Ćwiczenie w którym zakres sumowanych komórek (G31:G40) różni się od zakresu
komórek które mają sprawdzić podany warunek (E31:F40). Taka formuła pozwala na
zsumowanie elementów z jednego zakresu (kolumny ”G”) w zależności od warunku
nałożonego na elementy innej kolumny („E”).
2.
Obliczanie wartości bezwzględnej i silni.
Do obliczania wartości
bezwzględnej używamy
funkcji MODUŁ.LICZBY
a do obliczania silni
funkcji SILNIA
Działania wykonane są dla kilku różnych argumentów aby prześledzić i porównać wyniki, dla
wartości 170 komputer obliczy silnie a powyżej tej wartości otrzymujemy komunikat
o błędzie. Wynika to z przekroczenia zakresu liczb reprezentowanych w pamięci komputera.
3.
Dzielenie z resztą:
3.1. Resztę z dzielenia obliczamy korzystając z funkcji MOD(dzielna;dzielnik)(modulo),
natomiast wynik dzielenia całkowitego otrzymujemy stosując do wyniku dzielenia
funkcję LICZBA.CAŁK(dzielna/dzielnik), która obcina część całkowitą liczby.
4.
Liczby rzymskie
4.1. Eksel oferuje przekształcenie liczby dziesiętnej na liczbę rzymską za pomocą funkcji
RZYMSKIE, która zapisuje liczbę dziesiętną w postaci ciągu znaków
odpowiadających liczbie rzymskiej. Drugi argument funkcji RZYMSKIE(X;0) (liczba
od „0” do „4”) określa typ zapisu rzymskiego. Dla zapisu klasycznego stosuje się 0 a
dalej coraz bardziej uproszczony aż do poziomu 4.
5.
Liczby w systemie dwójkowym, ósemkowym i szesnastkowym
5.1.
5.2. W informatyce stosuje się zapisu licz w systemie dwójkowym (binarny). Do zapisu
wartości bajtów danych stosuje się system ósemkowy i szesnastkowy.
6.
Permutacje i kombinacje
6.1.
6.2. Kombinacja to ilość wszystkich możliwości wyboru (np. liczb) z określonego zbioru
bez zwracania uwagi na kolejność.
6.3. Funkcja permutacje oblicza wariancję bez powtórzeń. Wariancja to liczba wszystkich
możliwych ustawień (kolejności)tych elementów. (ilość możliwości wybrania „k”
różnych elementów z „n” (k<n) z uwzględnieniem różnych ich kolejności nazywamy w
matematyce wariancją bez powtórzeń).
7.
Funkcje trygonometryczne
7.1. Oblicz wysokość komina, jeżeli wiadomo, że z odległości dl=60m widać go pod kątem
α=560
zadanie najlepiej obliczyć z obowiązującymi w trójkącie prostokątnym zależności (x
szukana zależność) x = dl * TAN (α)
7.2.
7.3. Argumentem funkcji RADIANY jest wartość wyrażona w stopniach i odwrotnie dla
funkcji STOPNIE