Oddziaływanie elektronu z materią

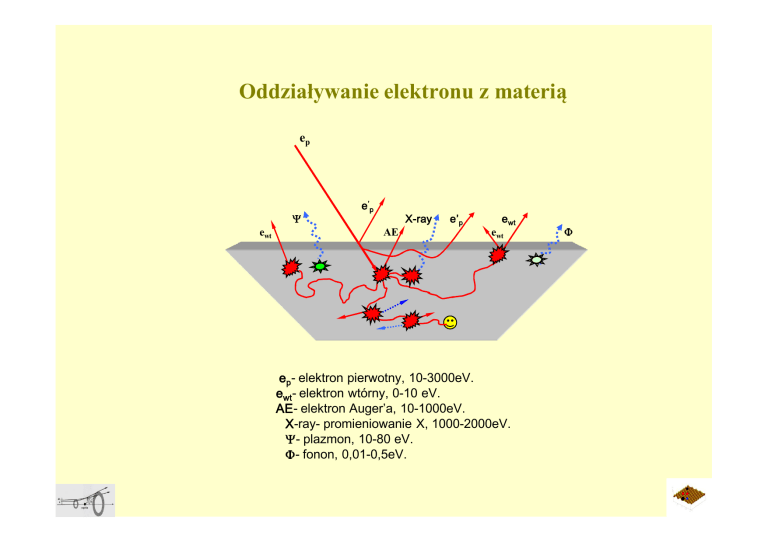
Oddziaływanie elektronu z materią
ep
e ’p
X-ray

ewt
AE
e’p
ewt
ewt
ep- elektron pierwotny, 10-3000eV.
ewt- elektron wtórny, 0-10 eV.
AE- elektron Auger’a, 10-1000eV.
X-ray- promieniowanie X, 1000-2000eV.
- plazmon, 10-80 eV.
- fonon, 0,01-0,5eV.

Zderzenie
Promieniowanie: 1. Energia: identyfikacja
2. Intensywność: analiza ilościowa
Oddziaływanie cząstek
b

T

Coulomb
Współczynnik
kolizji
Energia przekazywana
w trakcie oddziaływania
cząstek
Przekrój czynny
(prawdopodobieństwo
kolizji)
Średnia droga
swobodna cząstki
σ
liczba kolizji
liczba cząstek
zze
k
r
2
F
1
E
  ze
kin
2r
E
 mV
kin
2
2
2
k=1/4e =1 w układzie CGS:
e2 = 14,4 eVǺ
de Broglie
Bohr
Rutherford
Geiger
Marsden
2
2
2
p
2m
1/λ  σN'
Liczba centrów
oddziaływań
Prawdopodobieństwo oddziaływania
Pσ
liczba oddz.
liczba cz. pad. (I)
Liczba oddziaływań = INd
gdzie I -liczba cząstek padających, M1.
N- gęstość atomowa materiału M2.
N = NA/A
d - grubość warstwy materiału M2.
Energia oddziaływania
Elektrony:
E = mc2 = 0,511 MeV
E = mV2/2
V = p/m = h/m,  = h/p, czyli;
E = h2/2m 2 (Dla =1Å, E=149eV)
Fotony:
E = h = hc/ = 12,4/  [keV/Å]
1eV=1,610-19J
Oddziaływanie cząstka-cząstka (1)
M1, z1, v1, E1

M2

M2, z2, v2, E2
M1, z1, v, E
- kąt odbicia
 -kąt odrzutu
UKŁAD MUSI SPEŁNIAĆ ZASADY
ZACHOWANIA
1. ENERGII
M1v2 = M1v12 + M2v22
2. PĘDU
Składowe równoległe do toru:
M1v = M1v1cos + M2v2cos
Składowe prostopadłe do toru:
0 = M1v1sin + M2v2sin
Oddziaływanie cząstka-cząstka (2)
z1, p2
db
b
2b  db   ( )  2 sin   d 
(-) oznacza, że ze wzrostem b siła
oddziaływania i kąt  będą malały
d

z1, p1
z z e2
atom
z2
F 1 2
r2
gdzie r  b
Założenie: z1 jest w ruchu, z2 pozostaje w spoczynku, oddziaływania elastyczne.
p
p2
/2
p1; p1=M1v
p2=M1v1

1
p = M1vsin( /2)
2
p = 2M1vsin( /2)
Siła oddziaływania wynosi F  dp , czyli Δp   Fdt , (t – czas oddziaływania
dt
F- siła oddz. Prostopadła do toru cząstki)
z 1 z 2e 2
θ
Δp 
2cos
bv
2
gdzie v jest prędkością początkową jonu.
b=?
Oddziaływanie cząstka-cząstka (3)
z
F
0
0
M1v1
Δp 
 F
 (dp)
z
b
M1v
b
Δp 

r
 Fdt   F
z
cos  dt
dt 
F jest siłą skierowaną prostopadle
do rzeczywistego toru cząstki
[4] Δp 
czyli r  b !
 F cos 
dt
d
d
dt
d
d
z z e2
F 1 2
r2
z z e2
p  1 2
r2
[1]
Moment kątowy początkowy wynosi M1vb
Moment kątowy końcowy M1r2 dt/d.
z z e2
r2
 cos vbd  1vb2  cosd [7]
z1z 2e 2
[8] p 
(sin  2  sin 1 )
vb
+=1800,
Przyjmujemy że 1=-0, 2=+0, 20
czyli sin2-sin 1=2sin(900-1/2 )=2cos /2
M 1r 2
dt
 M 1 vb
d
czyli
dt
r2

d
vb
z1z 2e 2
p 
2 cos / 2
vb
cnd.
[9]
[5]
Oddziaływanie cząstka-cząstka (4)
z 1z 2e 2
θ
2 cos
p = 2M1vsin( /2) =
bv
2
θ
2
b
θ
2M 1 v 2 sin
2
z1z 2 e 2 2cos
Teoria Rutherford,
Potw. teor. Geiger
i Marsden 1911-1913
[9]
z 1z 2 e 2
θ
b
cot
2E
2
() = ?
 ( ) 
2b  db   ( )  2 sin   d 
sin   2 sin  / 2  cos / 2 
1
d
d cot  / 2   
2
2 sin  / 2
  
1  z 1z 2 e 2
 
2 E
2

1

 sin 4  / 2 

z 1z 2 e 2
Najmniejsze zbliżenie culombowskie: d 
E
Np.: d = 6,810-4Å dla jądra He o E=2MeV uderzającego w atom Ag
 = [2,84 born = 2,8910-24 cm2]
b
db

sin  d 
Oddziaływanie cząstka - jądro
Energia przekazana w kolizji;
Tmax 
dE kin

dx
n
4 M 1M 2
2
M 1  M 2 
E kin
4  . z1 2 z 2 2 e 4 N
b max


ln
b min
M 2v 2
gdzie N jest gęstością atomową.
2
2
z
z
e
1
2
b
 vp
min
4 z1 z 2 e 2
bmax 
2 mv 2 I
gdzie I jest energią przesunięcia jadra.
Oddziaływanie cząstka – elektron (1)
(Cząstka w ruchu)
Pęd przekazany w czasie kolizji;
2 z1e 2
p 
bV
V0  2 .e
Prędkość elektronu na orbicie
h
2

[1]
c
km
 2,2  10 3
137
s
Energia kinetyczna przekazana w czasie kolizji;
M zr 
me M j
me  M j
p 2
2 z12e 4
T

2m b 2 mV 2
[2]
d  (T )   2 bdb
[3]
T max
 n
Td 
T min
[4]
 me  m
Strata energii na jednostkę drogi;

dE kin
dx

n – liczba elektronów w jednostce objętości
dE kin

 n
dx
(Zmiana granic całkowania w [5] w porównaniu z [4].)
b max
2 T  bdb
b min

[5]
Oddziaływanie cząstka – elektron (2)
Z równań 2, 3, i 5 otrzymamy;
dE kin
4 . z1 2 e 4


n
dx
mV 2
bmax

bmin
1
db
b
2
dE kin 4π z1 e 4 n
b max



ln
dx
mV 2
b min
n – gęstość elektronowa
b min  ?
bmax  ?
[6]
Oddziaływanie cząstka – elektron (3)
p 2
2 z12e 4
T 

2 m b 2 mV 2
[2]
Obserwacje doświadczalne: bmin wtedy gdy prędkość przekazana elektronowi
wynosi 2V prędkości cząstki, a przekazana energia równa się
Tmax 1 m(2V )2  2mV2
2
[7]
Z równań [2] i [7] wynika, że
b min
z1e 2

mV 2
[8]
Obserwacje doświadczalne: Jeśli b dąży do maksimum to przekazana energia dąży
do minimum czyli do energii wzbudzenia I.
[9]
T min  I
Z równań [2] i [9] można wykazać, że
b max 
2 z1e 2
2 mV
2
[10]
I
Czyli, na podstawie [6], [8] i [10 wynika, że
2
dEkin 2π z12e4n
2mV


ln
I
dx
mV2
Dla przypomnienia: E=M1V2/2, a n=Nz2.
[11]
Oddziaływanie elektron – elektron (1)
E kin
db
m, V
b
p
mV

2
2
2e 2
p 
bV
2

p 
T
e4

2m
E kin b 2
z1=z2 i M1=M2=m
Przekrój czynny;
d  (T )   2 bdb
e4
2bdb  
dT
2
EkinT
e 4 dT
d T  
2
Ekin T
Oddziaływanie elektron – elektron (2)
Tmax
 
 d T 
Tmin
 [cm2=1024 barn]
e4
 
E kin
 1
1


 Tmin Tmax



Jeśli Tmax>>Tmin to
e4
1
6,5  10 14
 


Ekin Tmin
Ekin Tmin
Tmin = energia wiązania elektronu=EB
e 4
 
E kin E B
[cm2] [Energia w eV.]
Oddziaływanie elektron – elektron (3)
Energia zredukowana
U=Ekin/EB
to
Przekrój czynny (jedn. arb.)
e 4
 
2
UE B
0
1
2
U < 1, czyli  = 0
3
4
U=E/EB
5
6
7
8
Średnia droga swobodna elektronu  (1)
I  I o / 2,718
 dI  IN 'dx
gdzie N’ jest gęstością centrów oddziaływań
'
I  IoeN x
z definicji 1 /   N '
czyli
I  I o exp  x /  
Zależność  od energii kinetycznej elektronu
  f Ekin , Ewzb 
dE
1/    1  kin
Ewzb dx
Głównym powodem strat energii elektronów jest wzbudzenie plazmonów.
Ewzb  
gdzie  jest częstością drgań plazmonu
Średnia droga swobodna elektronu  (2)
dE
1/    1  kin
 dx
4
 dE  4e 2n ln B
dx mV
B
Ekin
Ewzb
2mV 2


gdzie n jest numerem orbity Bohra.
czyli
więc
2e2 2mV 2
dE

  2 ln

dx V
1  e2 ln 2mV 2
 V 2

Na przykład, jeśli e- / 350eV to  = 9Å
(ħ15eV, V2=2E/m)

1/ 2
 4e2n 

 
m 

Zależność średniej drogi swobodnej elektronu od jego
energii
Zależność średniej drogi swobodnej cząstki od kąta
padania.
I = I0exp(-d/)
I = I0exp(-d/cos)
d

deff