Twierdzenie sinusów

Twierdzenie sinusów
α
c
β
b
R
a
γ
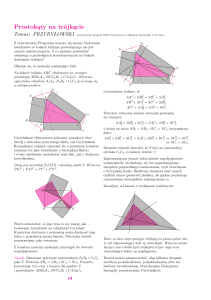
W każdym trójkącie zachodzi związek
a
b
c
=
=
= 2R
sin α sin β sin γ
Dowód
A
D
α
β
B
O
a
γ
C
Poprowadźmy średnicę CD. Kąt CBD jest wtedy prosty, bo oparty jest na średnicy okręgu (to wniosek z
twierdzenia o kącie wpisanym i środkowym. Kąt CDB jest oparty na tym samym łuku CB, co kąt CAB. Mają
więc równe miary.
∠CDB = ∠CAB = α
Z definicji sinusa kąta ostrego mamy:
sin ∠CDB =
sin α =
CB
CD
a
2R
Z tego wynika, że
a
= 2R
sin α
Analogiczne rozumowanie można przeprowadzić dla pozostałych boków i kątów.
Mamy więc:
b
= 2R
sin β
c
= 2R
sin γ
Widać, że można napisać:
a
b
c
=
=
= 2R
sin α sin β sin γ
Twierdzenie jest udowodnione. Przynajmniej dla trójkąta ostrokątnego. Ale, czy jest prawdziwe dla dowolnych trójkątów. Możesz sprawdzić, że dla trójkąta prostokątnego dowód jest trywialny (to takie specjalne
słowo często używane przez matematyków). Rozpatrzmy jeszcze przypadek trójkąta rozwartokątnego.
A
α
C
a
B
O
D
Tym razem kąt DBC jest prosty, oraz
BC
DC
a
sin ∠BDC =
2R
sin ∠BDC =
Co możemy powiedzieć o kącie BDC? Na czworokącie ABDC jest opisany okrąg. Jak udowodniono w innym
miejscu, wtedy suma przeciwległych kątów czworokąta wynosi 180°. Zatem
∠BDC + α = 180 °
∠BDC = 180 ° − α
Zatem
sin(180 ° − α ) =
a
2R
Wiemy, że sin(180 ° − α ) = sin α
Mamy więc:
a
. Tak samo jak dla trójkąta ostrokątnego. Pozostałe równości składające się na twierdzenie
sin α
sinusów w trójkącie rozwartokątnym dowodzi się analogicznie.
q.e.d.
sin α =