Rozwiązania przykładowych zadań Plik

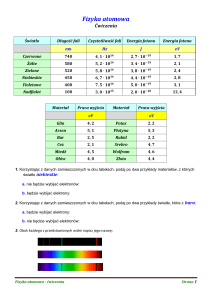
Zjawisko fotoelektryczne zewnętrzne i wewnętrzne – przykładowe rozwiązania zadań
Zadanie 1
Na powierzchnię magnezu pada promieniowanie o długości fali 200 nm. Oblicz energię kinetyczną
elektronu wybitego z powierzchni magnezu. Praca wyjścia elektronu magnezu wynosi 3,71 eV.
Dane:
  200nm  200 10 9 m
W  3,71eV  3,7 1,6 10 19 J  5,92 10 19 J
Szukana:
Ek  ?
Wzory:
h  W  Ek

c

Rozwiązanie:
Energię kinetyczną obliczymy przekształcając równanie Einsteina-Millikana, pamiętając o związku
między częstotliwością i długością światła:
h  W  Ek
Ek  h  W 
hc

W 
6,63 10 34 J  s  3 108
200 10 9 m
m
s  5,92 10 19 J
Ek  0,09945 10 17 J  5,92 10 19 J  9,945 10 19 J  5,92 10 19 J  4,025 10 19 J
Odpowiedź:
Energia kinetyczna wybitego z powierzchni magnezu elektronu wynosi 4,025 10 19 J .
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Zadanie 2
Promieniowanie o długości 232 nm pada na płytkę cynkową. W celu powrócenia wybitych elektronów
do płytki przykłada się do płytki napięcie hamujące o minimalnej wartości 2 V. Oblicz pracę wyjścia
elektronów z cynku.
Dane:
  232nm  232 10 9 m
U  2V
Szukana:
W ?
Wzór:
h  W  Ek
Związek pomiędzy energią potencjalną i napięciem hamującym:
E p  eU
Rozwiązanie:
Pracę wyjścia obliczymy z przekształconego wzoru Einsteina – Millikana:
W  h  Ek
Aby tego dokonać należy obliczyć energię fotonu i energię kinetyczną elektronów wybitych
z powierzchni płytki cynkowej. Energię fotonu obliczymy korzystając z zależności:

c
.
Jeśli chodzi o energię kinetyczną, to trzeba tu skorzystać z faktu, że energia ta równa jest energii
potencjalnej elektronu w polu elektrycznym wywołanym napięciem hamującym.
E k  E p  eU .
Zatem mamy:
W  h  E k 
hc

 eU 
6,63 10 34 J  s  3 108
232 10 9 m
m
s  1,6 10 19 J  2V  0,0857 10 17 J  3,2 10 19 J
W  5,37 10 19 J  3,36eV
Odpowiedź:
Praca wyjścia elektronu z powierzchni płytki cynkowej wynosi 3,36 eV.
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Zadanie 3
Oblicz minimalną wartość pędu fotonu, który padając na wykonaną z cezu katodę fotokomórki
spowoduje przepływ prądu. Praca wyjścia elektronu z cezu wynosi 2,14 eV.
Dane:
W  2,14eV  3,424 10 19 J
Szukana:
pmin  ?
Wzór:
W  h  Ek
p

h

c

Rozwiązanie:
Ponieważ mamy obliczyć minimalną wartość pędu, wynika stąd, że Ek=0. Zatem:
W  h
Zależność pędu i częstotliwości fotonu można wyznaczyć z następujących rwności:
h
   p  h

c
c
  

p
Z otrzymanego związku wyznaczmy częstotliwość:

pc
h
i wstawmy do równania:
W  h  h
pc
 pc
h
czyli:
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
p
W 3,424 10 19 J

 1,14 10 27
m
c
3 108
s
m2
s 2  1,14 10 27 kg  m
m
s
s
kg 
Odpowiedź:
Minimalna wartość pędu fotonu, która spowoduje przepływ prądu w fotokomórce, w której katoda
wykonana jest z cezu wynosi: 1,14 10  27 kg 
m
.
s
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego