praca-licencjacka

Wykład 13.
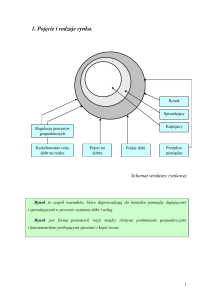
Pajęczynowy model równowagi rynkowej
Poprzednio prowadząc rozważania dotyczące równowagi rynkowej przyjmowaliśmy, że
producenci natychmiast reagują na zmiany ceny rynkowej zmianą wielkości podaży. Dotyczyło to
również nabywców. O ile jednak w realnych warunkach jest tak, że nabywcy prawie natychmiast po
zmianie ceny zmieniają wielkość swoich zamówień to w odniesieniu do wielu producentów jest to
założenie daleko odbiegające od rzeczywistości. Dotyczy to szczególnie tych przypadków, kiedy cykl
produkcyjny jest długi, wynosi kilka lub nawet kilkanaście miesięcy. W takim okresie sytuacja na rynku
może się istotnie zmienić. Dlatego wytwórcy tego typu dóbr zazwyczaj starają się zabezpieczyć przed
niespodziewanymi zmianami na rynku poprzez podpisywanie jeszcze przed rozpoczęciem produkcji
umów na wykonanie określonego dzieła z podaniem ceny po jakiej zostanie ono sprzedane. Są jednak
działy produkcji, kiedy takie rozwiązania są jeszcze stosunkowo rzadko stosowane. W Polsce przykładem
tego typu rynków jest rynek rolno-spożywczy a zwłaszcza mięsny. W tym ostatnim przypadku cykl
produkcyjny trwa kilkanaście miesięcy. Na przykład rolnik decydujący się na rozpoczęcie tuczu
określonej ilości prosiąt nie zna ceny po której będzie sprzedawał swoją trzodę, gdy dojdzie ona do
odpowiedniej wagi. Obserwacje praktyki doprowadziły do wniosku, że większość rolników
prowadzących na małą skalę hodowlę przy decyzji o wielkości hodowli kieruje się głównie aktualnymi
cenami. Zazwyczaj nie uwzględniają oni tego, że jeżeli produkcja teraz jest opłacalna to przyciągnie
nowych producentów i najprawdopodobniej cena w przyszłości będzie mniej korzystna. Ten sam sposób
myślenia dominuje również w okresach niskiej opłacalności produkcji. Niski procent producentów
rozpoczyna wtedy produkcję przewidując, że niska cena dzisiaj zniechęci wielu innych dostawców
danego produktu i tym samym za pewien okres można się spodziewać korzystnego wzrostu cen.
Zobaczmy, jak funkcjonuje tego typu rynek. Aby symulować w możliwie prosty sposób opisane
wyżej mechanizmy przyjmijmy następujące założenia:
1. Producenci ustalają optymalną wielkość produkcji w oparciu o cenę z bieżącego okresu ale do
sprzedaży dochodzi dopiero w następnym.
2. Produkt nie nadaje się do długiego magazynowania i dlatego musi być sprzedany w danym okresie (nie
można go przechować do następnego okresu).
3. Funkcje podaży i popytu są prostymi o typowym nachyleniu.
Prowadzone rozważania ilustruje rys. 1. Przyjmijmy, że cena w okresie wyjściowym wynosi
p0. Zgodnie z założeniem 1 odczytujemy na funkcji podaży Y wielkość produkcji jaka pojawi się na
rynku w okresie 1. Będzie to Y1. Konfrontując tą wielkość z popytem jaki będzie występował przy cenie
p0 stwierdzimy, że cena p0 jest za wysoka, gdyż nie cała podaż znajdzie nabywców.
Aby zrównoważyć rynek cena musi spaść do poziomu p1, gdyż tylko wtedy popyt będzie wynosił
tyle ile podaż. Spadek ceny z poziomu p0 do p1 spowoduje, że producenci kierując się tą ostatnią ceną na
okres 2 przygotują produkcję o wielkości Y2. Z poprzednich ustaleń wiemy jednak, że po cenie p1 można
sprzedać nie tylko Y2 ale Y1. Tym razem producenci będą mogli podnieść cenę, gdyż przy cenie p1 popyt
jest większy niż podaż. Oferując produkcję o wielkości Y2 mogą ją sprzedać po cenie p2. Ten wzrost ceny
(w porównaniu do p1) zachęci oferentów do zwiększenia produkcji do wielkości Y3. Tej podaży nie będą
jednak w stanie sprzedać po cenie p2, gdyż wtedy popyt jest mniejszy od podaży. Muszą oni obniżyć cenę.
Kontynuując to rozumowanie będziemy krążyć dookoła punktu równowagi wyznaczonego przez cenę p*
i obroty X*=Y*. Na rys. 1.
przyjmuje to postać spirali, pajęczyny (stąd nazwa modelu). Widać
wyraźnie, że ta spirala stopniowo zbliża się do punktu równowagi, czyli mówimy, że spirala się zwija.
Jest tylko kwestią czasu kiedy dojdzie ona do punktu przecięcia się funkcji podaży i popytu. Warto
zauważyć, że po dojściu do tego punktu układ się ustabilizuje. Aby się o tym przekonać wystarczy
zauważyć, że gdy cena obecna będzie wynosiła p*, to producenci przygotują na następny okres produkcję
o wielkości Y*. Teraz jednak odmiennie niż poprzednio tą produkcję będą mogli sprzedać po cenie p*.
Rynek nie będzie jej korygował w dół ani w górę, gdyż obecna podaż będzie równa przyszłemu popytowi.
Powyższy opis działania mechanizmu rynkowego w sytuacji przedstawionej na rys. 1 pozwala
nam stwierdzić, że ta równowaga rynkowa będzie stabilna, gdyż w przypadku jej zakłócenia siły rynkowe
automatycznie będą ją przywracać.
Przed sformułowaniem następnych wniosków rozpatrzmy inny przypadek, różniący się od
powyższego tylko tym, że teraz funkcja popytu będzie bardziej stroma niż funkcja podaży. Przedstawia to
rys. 2.
Ponownie rozpoczynamy analizę od ceny p0. Na jej podstawia producencie przygotują
produkcję o wielkości Y1. Nie da się jej sprzedać po cenie p0. Musi ona zostać obniżona do poziomu p1.
Sugerując się tą ostatnią ceną producenci w następnym okresie wystąpią z podażą o wielkości Y2. Gdyby
utrzymali cenę p1, to powstałaby nadwyżka popytu nad podażą, dlatego rynek podniesie cenę do poziomu
p2. Ta wyższa cena skłoni producentów do zwiększenia produkcji do wielkości Y3. Jej sprzedanie będzie
wymagało obniżenia cen.
Kontynuując to rozumowanie zauważymy, że teraz też krążymy dookoła punktu równowagi ale
tym razem coraz bardziej oddalamy się od niego. Spirala na rys. 2 stopniowo rozwija się. Możemy więc
stwierdzić, że układ wytrącony z punktu równowagi nie powraca samoczynnie do niego, czyli ten
przypadek jest przykładem niestabilnej równowagi rynkowej.
Jeszcze raz przypomnijmy, że jedyna różnica między przypadkami przedstawionymi na rys. 1 i 2
polega na tym, iż w pierwszym przypadku funkcja podaży była bardziej stroma od funkcji popytu (układ
był stabilny - spirala zwijała się) a w drugim było odwrotnie (układ niestabilny - spirala rozwija się). Jak
widać pominęliśmy w rozważaniach przypadek pośredni, gdy obie funkcje są tak samo strome, czyli w
przypadku funkcji prostoliniowych oznacza to, iż wartość bezwzględna współczynników kierunkowych
obu prostych jest identyczna. W takim przypadku spirala nie będzie się zwijała ani rozwijała, czyli będzie
krążyć po swoim śladzie. Taki układ nazwiemy również niestabilną równowagą, gdyż układ wytrącony z
równowagi nie będzie samoczynnie do niej powracał.
Jeżeli chcielibyśmy zobrazować zmiany cen w czasie dla podanych wcześniej przypadków, to
można to zrobić w sposób ukazany na rys. 3a i 3b.
Powyższe rysunki bardzo przypominają wykresy zmian cen np. wieprzowiny. Takie wahania
rynku są źle oceniane tak przez producentów jak i nabywców. Sytuację poprawia rozwój giełd
towarowych na których handluje się standaryzowanymi towarami, zazwyczaj przygotowanymi do
długiego magazynowania. Fachowcy grający na takiej giełdzie w okresach niskich cen skupują towar aby
go sprzedać w nadchodzącym okresie zwyżki cen albo podpisują z producentami umowy terminowe na
odbiór w przyszłości produktów po określonej cenie. Tego typu działania zazwyczaj mają stabilizujący
wpływ na rynek.
Innym sposobem stabilizacji rynku jest powołanie instytucji rządowej dokonującej
interwencyjnych zakupów (w okresie zniżek cen) lub sprzedaży (gdy cena nadmiernie rośnie). Skutki
takich działań pokażemy na prezentowanym poprzednio przykładzie (zob. rys. 1), który teraz
zmodyfikujemy przyjmując, że Agencja Rynku Rolnego będzie w okresach nadprodukcji skupowała
część nadwyżki podaży, by sprzedać ją w okresach niedoboru produkcji. Prezentuje to rys. 4.
Zobaczmy najpierw, co stałoby się gdyby Agnacja Rynku Rolnego skupiła w pierwszym okresie
połowę nadwyżki podaży, która powstała w wyniku tego, że producenci spodziewając się ceny p0 przygotowali podaż w ilości Y1. Wielkość interwencyjnego skupu pokazuje strzałka I1. Wtedy na rynek
faktycznie trafiłaby podaż w ilości Y11, co wywołałoby spadek cen z poziomu p0 do p11 zamiast do p1
(gdyby interwencji nie byłoby). Na rys. 4. łatwo można dostrzec, że ukształtowanie się w pierwszym
okresie ceny p11 spowoduje, że producenci na następny okres przygotują podaż w ilości przekraczającej
popyt przy tej cenie. Oznaczałoby to, że w drugim okresie konieczny byłby interwencyjny skup. Agencja
nie mogłaby sprzedać nadwyżek, które zgromadziła w poprzednim okresie. Jeżeli ta agencja dysponowałaby środkami finansowymi i materialnymi (wolne magazyny) pozwalającymi na ponowny skup, to
postępując w ten sposób można doprowadzić rynek do punktu równowagi. Efektem tego będzie jednak
stałe utrzymywanie się wysokich zapasów, których nie będzie można sprzedać na rynku danego kraju.
Jedynym wyjściem jest eksport zgromadzonych nadwyżek. Z czysto ekonomicznego punktu widzenia
taka interwencja jest nieracjonalna.
Lepszym rozwiązaniem jest ustalenie interwencyjnego skupu na takim poziomie aby złagodzić
spadek cen ale tylko na tyle, że w następnym okresie pojawi się niedobór podaży, który pozwoli sprzedać
zgromadzone nadwyżki redukując tym samym wielkość niedoboru. Tak się stanie gdy interwencyjny skup
towaru w pierwszym okresie wyniesie np. I2 (krótsza strzałka). Wtedy cena spadnie do poziomu p12. Na
podstawie tej ceny w drugim okresie pojawi się podaż w ilości Y12, którą Agencja Rynku Rolnego
zwiększy o zgromadzone wcześniej rezerwy. To spowoduje, że cena wzrośnie ale mniej niż gdyby nie
było tej interwencji. Kontynuując to rozumowanie doprowadzimy do ukształtowania się na rynku ceny p*
i wielkości obrotów X*=Y*.
Przedstawiony przypadek może być również ilustracją pokazującą jak trudno jest przeprowadzić
skuteczne równoważenie rynku. Z powyższego rozumowania wynika m.in wniosek, że formułowane
bardzo często postulaty aby interwencja Agencji Rynku Rolnego była tak duża aby utrzymać cenę, przy
której wystąpiła nadwyżka podaży są całkowicie nieracjonalne z ekonomicznego punktu widzenia,
zwłaszcza w dłuższym okresie czasu.