Praca, moc, energia

Praca, moc, energia
1. Klasyfikacja energii.
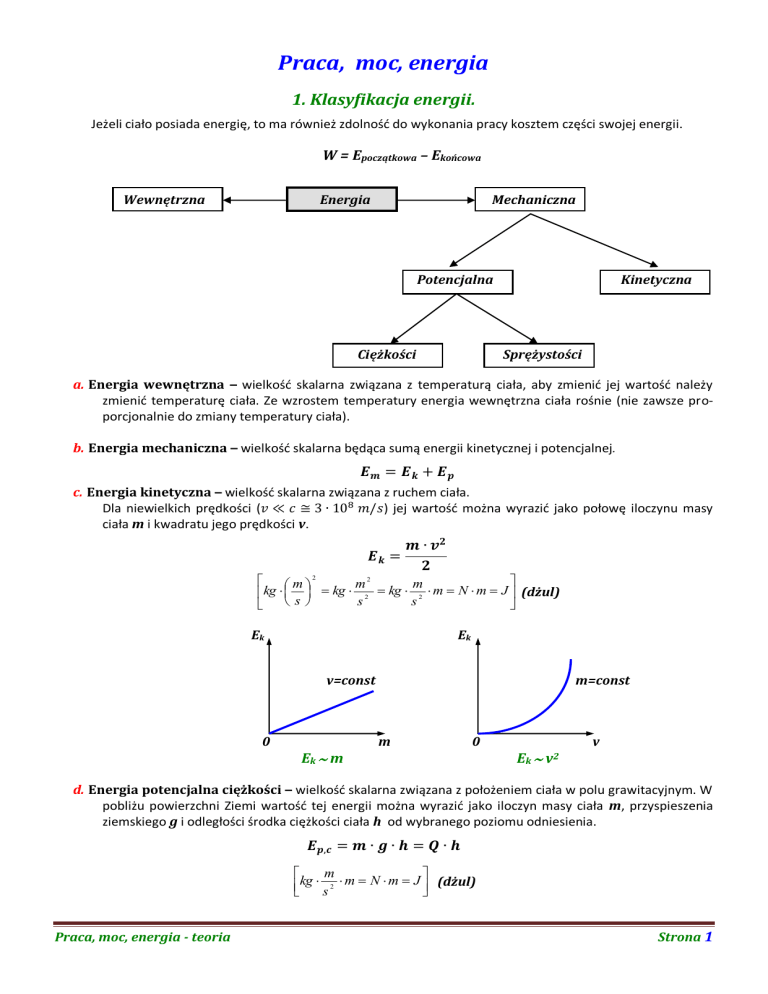
Jeżeli ciało posiada energię, to ma również zdolność do wykonania pracy kosztem części swojej energii.
W = Epoczątkowa – Ekońcowa
Wewnętrzna
Energia
Mechaniczna
Potencjalna
Ciężkości
Kinetyczna
Sprężystości
a. Energia wewnętrzna – wielkość skalarna związana z temperaturą ciała, aby zmienić jej wartość należy
zmienić temperaturę ciała. Ze wzrostem temperatury energia wewnętrzna ciała rośnie (nie zawsze proporcjonalnie do zmiany temperatury ciała).
b. Energia mechaniczna – wielkość skalarna będąca sumą energii kinetycznej i potencjalnej.
c. Energia kinetyczna – wielkość skalarna związana z ruchem ciała.
Dla niewielkich prędkości (
) jej wartość można wyrazić jako połowę iloczynu masy
ciała m i kwadratu jego prędkości v.
2
2

 m   kg  m  kg  m  m  N  m  J 
kg

 

 (dżul)
2
2
s
s
s


Ek
Ek
v=const
0
Ek  m
m=const
m
0
Ek 
v
v2
d. Energia potencjalna ciężkości – wielkość skalarna związana z położeniem ciała w polu grawitacyjnym. W
pobliżu powierzchni Ziemi wartość tej energii można wyrazić jako iloczyn masy ciała m, przyspieszenia
ziemskiego g i odległości środka ciężkości ciała h od wybranego poziomu odniesienia.
m


kg  s 2  m  N  m  J  (dżul)
Praca, moc, energia - teoria
Strona 1
e. Energia potencjalna sprężystości – wielkość skalarna. W przypadku sprężyny jej wartość można wyrazić
jako połowę iloczynu współczynnika sztywności (sprężystości) sprężyny k i kwadratu zmiany jej długości
, na skutek jej rozciągania lub ściskania ( zmianę długości należy liczyć od stanu, gdy nie była poddana
działaniu siły rozciągającej lub ściskającej).
Wartość współczynnika k (wyrażanego w N/m) określa siły o jakiej wartości należałoby użyć, aby ją
rozciągnąć sprężyści o 1 metr. Wartość współczynnika sztywności zależy od rodzaju materiału, z którego
wykonano sprężynę, średnicy drutu, średnicy zwoju i liczby zwojów.
N

2
 m  m  N  m  J  (dżul)
2. Praca.
Założenie: na ciało o masie m działa stała, co do wartości, kierunku i zwrotu siła
. Pod działaniem
tej siły ciało przemieszcza się po linii prostej. Oznacza to, że kąt
pomiędzy kierunkiem ruchu ciała a
kierunkiem działania rozpatrywanej siły jest stały:
. Ponadto przemieszczenie ciała jest równe, co do
wartości przebytej drodze:
.

Wartość pracy wykonanej przez siłę

można obliczyć (przy powyższych założeniach) ze wzoru:
ż
Analiza możliwych przypadków:
  0 o  cos   1  W  F  r  0
a.
  0 o ;90 o     1;0  W  0

b.
  90 o  cos  0  W  0

c.
d.
  90 o ;180 o     0;-1  W  0


e.
  180 O  cos  -1  W  F  r  0
Praca, moc, energia - teoria
Wynika stąd, że praca może przyjmować
wartości dodatnie, ujemne i zerowe. Na przykład, gdy ciało spada, to jego ciężar wykonuje
pracę dodatnią (=0˚), podczas gdy siły oporu
powietrza w tym samym czasie wykonują pracę ujemną (=180˚). Jeśli ciało wspina się na
równię pochyła, to jego ciężar wykonuje pracę
ujemną ((90˚;180˚)), a siły sprężystości
podłoża zerową (=90˚).Gdy ciało zjeżdża
z równi pochyłej, to jego ciężar wykonuje pracę
dodatnią ((0˚;90˚)).Siły tarcia (oporów
ruchu) zawsze wykonują pracę ujemną
(=180˚).
Strona 2
Interpretacja geometryczna wykresu
Założenie: na ciało o pewnej masie, mogące się poruszać wzdłuż osi S (zgodnie z jej zwrotem), działa stała co
do wartości, kierunku i zwrotu siła . Składowa tej siły równoległa do kierunku ruchu jest wektorem niezerowym.
Możliwe przypadki:
Współrzędna tej siły na kierunku równoległym
do kierunku ruchu jest dodatnia.
Współrzędna tej siły na kierunku równoległym do
kierunku ruchu jest ujemna.
Jeżeli dany jest wykres
, to miarą pracy wykonanej przez składową równoległą
siły (do kierunku ruchu) jest pole figury ograniczone przebiegiem tego wykresu i osią S.
Pracę o wartości
wykonała składowa równoległa do kierunku ruchu, której współrzędna była dodatnia. Z
kolei pracą o wartości
wykonała składowa równoległa do kierunku ruchu, której współrzędna była
ujemna.
Uwaga:
a. Wartość pracy wykonanej przez składową prostopadłą do kierunku ruchu jest zerowa, gdyż kąt pomiędzy
wektorami
i
jest zawsze kątem prostym.
b. Nie mając dodatkowych informacji, z powyższego wykresu nie można wnosić, czy na rozpatrywane ciało
działała stała czy zmienna siła oraz po jakim torze się poruszało. Dlatego, na podstawie tego typu wykresu, można również obliczać pracę sił zmiennych działających na ciało nie poruszające się po linii prostej.
Praca, moc, energia - teoria
Strona 3
3. Moc.
Moc (średnia) – wielkość skalarna, definiowana jako iloraz wykonanej pracy i czasu, w którym ta praca została
wykonana.
ś
Korzystając z wzoru definicyjnego pracy otrzymuje się ponadto:
ś
Ale iloraz wartości przemieszczenia ciała i czasu w którym się dokonało, jest wartością prędkości średniej.
ś
Stąd:
ś
ś
4. Związek pomiędzy pracą a energią.
4.1 Sens fizyczny energii potencjalnej ciężkości.
Założenie: ciało o masie m jest podnoszone pionowo do góry (w pobliżu powierzchni Ziemi) ruchem
jednostajnym prostoliniowym przez pewną siłę zewnętrzną
. W ciągu pewnego czasu ciało przemieściło
się z wysokości h1 na wysokość h2.
(t2)
h2
(t1)
h1
Zgodnie z pierwszą zasadą dynamiki na ciało poruszające
się ruchem jednostajnym prostoliniowym, działają siły równoważące się, dlatego:
Ponadto z przyjętych założeń i rysunku wynika, że:
oraz
Z wzoru definicyjnego pracy mamy:
Jeśli założymy, że h1 = 0 i h2 =h (poziom odniesienia można przyjąć dowolnie), to mamy:
Można zatem powiedzieć, że energia potencjalna jaką ma ciało, jest równa co do wartości pracy
jaką trzeba wykonać, aby ciało o masie m podnieść ruchem jednostajnym na wysokość h w pobliżu powierzchni Ziemi (przypisując poziomowi początkowemu wartość zero).
Praca, moc, energia - teoria
Strona 4
3.2 Sens fizyczny energii kinetycznej.
Założenie: na ciało o masie m, mogące się poruszać wzdłuż poziomej powierzchni, działa stała siła wypadkowa o
niezerowej wartości
. Siła wypadkowa ma kierunek i zwrot zgodny z kierunkiem i zwrotem
wektora przemieszczenia ciała . W chwili początkowej (t1) prędkość ciała wynosiła v1.
(t1)
(t2)
Z przyjętych założeń wynika, że:
oraz, że wartość energii potencjalnej rozpatrywanego ciała nie ulegała zmianie:
Ponadto, z drugiej zasady dynamiki Newtona wynika, że:
Zatem praca wykonana przez siłę wypadkową poszła na zmianę energii kinetycznej ciała.
Wartość pracy wykonanej przez siłę wypadkową można wyrazić następująco:
Jeśli teraz założymy, że v1 = 0 i v2 = v, to otrzymamy:
Można zatem powiedzieć, że energia kinetyczna jaką ma ciało jest równa pracy jaką wykonała stała
siła wypadkowa, podczas rozpędzania ciała o masie m (początkowo nieruchomego) do prędkości v.
3.3 Praca niezrównoważonej siły zewnętrznej.
Założenie: na ciało o masie m poruszające się do pionowo do góry działa niezrównoważona siła zewnętrzna
W chwili początkowej t1 ciało znajdowało się na wysokości h1 i miało prędkość v1, a w chwili t2 (t2 > t1)
było na wysokości h2 i miało prędkość v2 (v2>v1).
Praca, moc, energia - teoria
.
Strona 5

Fz
Z przyjętych założeń i rysunku wynika, że:

v2
(t2)
h2

Q

Fz

Δr

v1
(t1)
Z drugiej zasady dynamiki:
h1

Q
Stąd:
v2  v1
 m  g  h2  h1  
2a
2
ma
2
Wynika stąd, że zmiana energii mechanicznej (Em) ciała (układu ciał) jest równa co do wartości pracy wykonanej przez siłę zewnętrzną nad tym ciałem (układem ciał).
3.4 Zasada zachowania energii mechanicznej.
Z wzoru:
wynikają następujące wnioski:
a. jeżeli siła zewnętrzna wykonuje nad ciałem pracę dodatnią, to energia mechaniczna tego ciała rośnie, gdy
natomiast praca tej siły jest ujemna, to energia mechaniczna tego ciała maleje,
b. jeśli praca siły (sił) zewnętrznej jest równa zeru, to:
ostatecznie:
Jeżeli na ciało (układ ciał) nie działają żadne siły zewnętrzne lub praca tych sił jest zerowa, to energia mechaniczna ciała (układu ciał) jest stała tzn. nie ulega zmianie wraz z upływem czasu – zasada zachowania energii
mechanicznej.
Wynika stąd również, że jeśli:
Zatem, jeżeli energia mechaniczna ciała jest stała, to wzrostowi energii kinetycznej odpowiada (w tym samym
czasie) taki sam co do wartości spadek energii potencjalnej i na odwrót.
Praca, moc, energia - teoria
Strona 6