otwórz

„EUROELEKTRA”
OLIMPIADA ELEKTRYCZNA I ELEKTRONICZNA
Rok szkolny 2006/2007, drugi etap, zadania dla grupy elektrycznej
Rozwiązania zadań
Zadanie 1
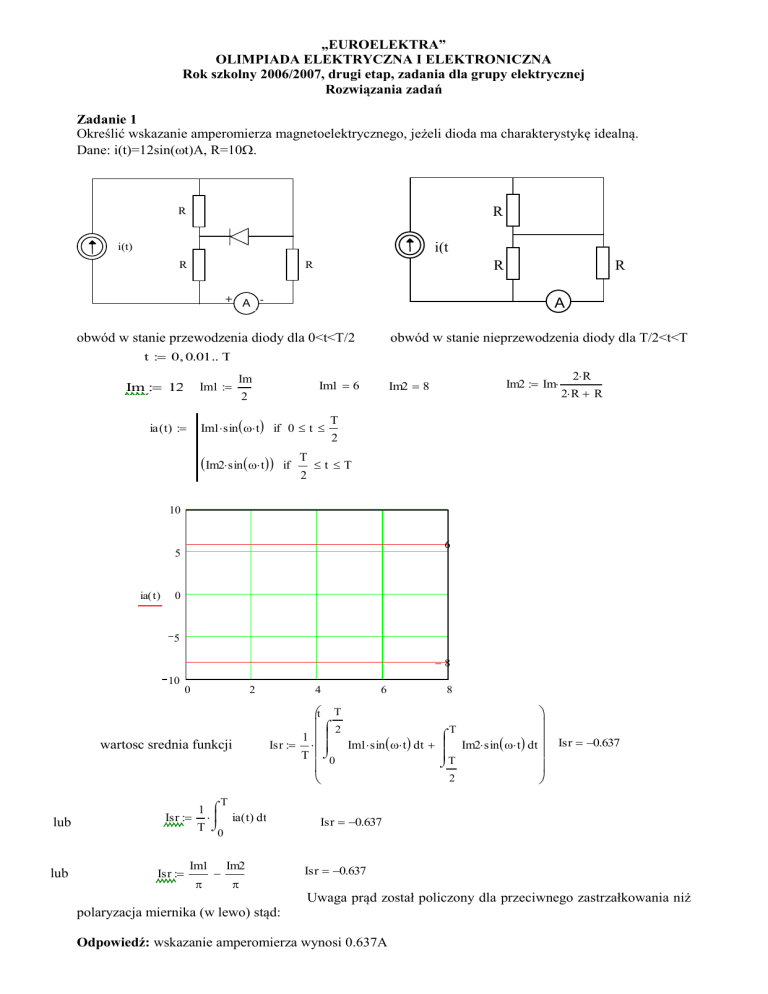
Określić wskazanie amperomierza magnetoelektrycznego, jeżeli dioda ma charakterystykę idealną.
Dane: i(t)=12sin(t)A, R=10
R
R
i(t
)
i(t)
R
R
R
+ A -
R
A
obwód w stanie przewodzenia diody dla 0<t<T/2
obwód w stanie nieprzewodzenia diody dla T/2<t<T
t  0 0.01 T
Im
Im1 
Im  12
Im1  6
2
Im1 sin   t if 0  t 
ia ( t) 
Im2  Im
Im2  8
 Im2 sin  t 
if
T
2
2 R
2 R  R
T
2
t T
10
6
5
ia( t )
0
5
8
10
0
2
wartosc srednia funkcji
4
6
t T
 2
1 
Isr    Im1 sin   t d t 
T  0


8
T


T

2


 Isr  0.637
Im2 sin   t d t



T
lub
Isr 
1 
  ia( t) d t
T 
Isr  0.637
0
lub
Isr 
Im1


Im2

Isr  0.637
Uwaga prąd został policzony dla przeciwnego zastrzałkowania niż
polaryzacja miernika (w lewo) stąd:
Odpowiedź: wskazanie amperomierza wynosi 0.637A
Zadanie 2
Indukcyjność poszczególnych układów wynosi:
La 
z  Φa
z 2  μ r μ 0 S

i
l1  l 2
Gdzie: a, b -strumień magnetyczny.
z - liczba zwoi.
S – przekrój rdzenia.
r - przenikalność magnetyczna względna.
0 - przenikalność magnetyczna próżni.
l1,l2 – długość drogi strumienia magnetycznego.
z  Φ b z 2  μ r μ 0 S
Lb 

l l
i
l1  1 2
l1  l 2
a ponieważ
stąd
l1  l 2
 l2 ,
l1  l 2
Lb>La
Odp. Układ z rysunku b). ma większą indukcyjność własną.
Zadanie 3
Należy sformułować równania opisujące w stanie ustalonym zmianę prądu cewki L:
a) w czasie przewodzenia klucza S1 (klucz S2 jest wyłączony),
b) w czasie przewodzenia klucza S2 (klucz S1 jest wyłączony)
Wzory te mają postać:
Dla przypadku a):
I L 
U we  U wy
L
 tON
(1)
Dla przypadku b):
I L 
U wy
L
 TS  tON 
(2)
Przyrównując prawe strony wzorów uzyskuje się
U
we
 U wy  tON 
U wy
L
 TS  tON 
(3)
stąd
U wy  U we 
t ON
 U we  d
TS
Odpowiedni wykres pokazano na rys.1.
Uwy
Uwe
d
0
1
(4)
Zadanie 4
I n  24 A
U p  1,76mV
1
1
 I n   24 A  2,4 A
10
10
U
1,76  10 3V
Rp  p 
 0,7333  10 3   0,7333m
Ip
2,4 A
Ip 
  0,0172  10 6   m
s  2,5mm2  2,5  10 6 m 2
R p  s 0,7333  10 3   2,5  10 6 m 2
x
Rp     x 

 0,1066m  10,66cm
s

0,0172  10 6   m
Odp: x=10,66 cm
Zadanie 5
Napięcie wtórne przy biegu jałowym wyniesie:
UG/UD = k  zG/zD
UD = UG/ (k  zG/zD) gdzie k = 2/√3 (współczynnik k można stosunkowo łatwo
wyprowadzić z wykresu wskazowego) UD = 15000/((2/√3) 50)) = 259,8V.
Maksymalny spadek napięcia (przy mocno indukcyjnym cosφ ) jest równy napięciu zwarcia a więc:
UDmin = UD (1- uz )
UDmin = 259,8  0,95 = 246,8V.
Zadanie 6
Przy pomocy multipleksera o 3 wejściach adresowych oraz dowolnych bramek zbuduj układ kombinacyjny
realizujący funkcję
y (d , c, b, a)   0, 1, 2, 5, 6, 9, 10, 12 .
Na wejścia adresowe multipleksera o wagach 22, 21, 20 podajemy odpowiednio sygnały wejściowe d, c, b.
Wejścia informacyjne multipleksera Di należy wyrazić przy pomocy sygnalu a, czyli szukamy Di = f(a),
przy czym i = 0, 1, 2, ...,7.
Lp.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
d
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
c
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
b
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
a
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
y
0
0
0
1
1
0
0
1
1
0
0
1
0
1
1
1
D0(a) = 0
D1(a) = a
D2(a) = a
D3(a) = a
D4(a) = a
D5(a) = a
D6(a) = a
D7(a) = 1
Schemat układu
a
"1"
"0"
b
c
d
A (20) D0D D1 D2 D3 D4 D5 D6 D7
0
B (21)
74151
S
2
C (2 )
W
Y
y= D
I
DI
Na podstawie wykresu z rys.2b należy stwierdzić, że wartość średnia czyli wskazanie woltomierza
magnetoelektrycznego wynosi 0.