Ruch obrotowy i orbitalny Ziemi
Ruch dobowy sfery niebieskiej jest pozorny wynika z obracania się Ziemi wokół własnej
osi z okresem równym 1 dobie gwiazdowej.
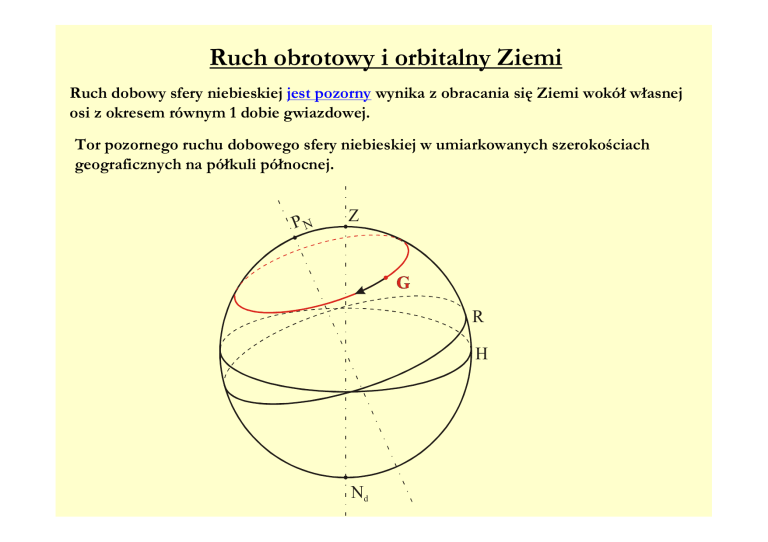
Tor pozornego ruchu dobowego sfery niebieskiej w umiarkowanych szerokościach
geograficznych na półkuli północnej.
PN
Z
R
H
Nd
Przykłady pozornego dobowego ruchu sfery niebieskiej
Na równiku
Na biegunie
Z=PN
Z
R
H=R
Nd
PN
H
Nd
Ruch orbitalny Ziemi
Tak jest w rzeczywistości
Tak wygląda to na sferze niebieskiej
Okres pomiędzy dwoma górowaniami gwiazdy równy jest 1 dobie gwiazdowej.
Doba słoneczna to okres pomiędzy dwoma kolejnymi górowaniami Słońca.
Górowanie – to przejście ciała niebieskiego przez południową gałąź południka
miejscowego. Zjawiska ruchu dobowego (w tym górowanie) zostaną omówione w
dalszej części wykładu.
Doba słoneczna jak wynika z rysunku jest dłuższa od doby gwiazdowej o wartość
dobowego przesunięcia Słońca po ekliptyce wynikającego z jego pozornego ruchu
rocznego, które wynosi:
360o
∆T =
= 0o986 = 3m57 s
365,24...
365,24... – długość tzw. roku zwrotnikowego czyli średnia długość roku kalendarzowego
Długość doby gwiazdowej wynosi więc średnio 23h56m03s czasu słonecznego. Czas
gwiazdowy i słoneczny będzie przedmiotem rozważań przedstawionych w dalszej
części wykładu.
Zjawiska ruchu dobowego
Kulminacja
Półkula północna
Kulminacja górna na południe od zenitu δ1 < ϕ , z1 = ϕ − δ
Kulminacja górna na północ od zenitu
δ2 > ϕ , z 2 = δ − ϕ
Kulminacja dolna: zawsze z3 = 180o − (ϕ + δ )
Wschody i zachody
Definicja
Wschód gwiazdy
dz
o
<0
z = 90
dt
Zachód gwiazdy
z = 90 o
Półkula północna
Gwiazdy nie zachodzące δ ≥ 90o − ϕ
Gwiazdy wschodzące i zachodzące ϕ − 90o < δ < 90o − ϕ
Gwiazdy nie wschodzące δ ≤ ϕ − 90o
dz
>0
dt
Obliczenie efemeryd wschodu i zachodu
Przejście przez I wertykał
Definicja – I wertykał jest to koło wielkie
przechodzące przez zenit i nadir
prostopadłe do południka miejscowego, a
więc A = ±90 o
Warunki:
δ < ϕ , A = ±90 o
ELONGACJE
o
Definicja: q = ±90
Warunki δ > ϕ
półkula północna
Precesja, nutacja, ruch bieguna
1.Precesja i nutacja
Kształt Ziemi zbliżony jest do elipsoidy obrotowej. W dużym przybliżeniu
można przedstawić ją jako jednorodną kulę ze zgrubieniami równikowymi.
Słońce, Księżyc i planety poruszają się bądź w płaszczyźnie ekliptyki bądź w
jej pobliżu.
Gdyby Ziemia była jednorodną kulą to wypadkowa sił przyciągania przez
Słońce i Księżyc przechodziłaby przez jej środek, zaś w środku masy siły
przyciągania przez Księżyc i Słońce równoważyłyby się z silą odśrodkową
wynikająca z jej ruchu orbitalnego.
Na zgrubieniach równikowych siły te nie równoważą się (patrz rysunek)
Mechanizm precesyjno-nutacyjny
na rysunku zaznaczona jedynie precesja księżycowo-słoneczna
Oznaczenia: M 1 - moment siły wywołany przez siły R1 R2
F1,F2 - siły przyciągania grawitacyjnego
C1,C2 - siły odśrodkowe gdzie:
C=F - w środku mas Ziemi
F1 >F2
C2 >C1
,
A więc:
R1 =F1 −C1 - skierowana jest do ciała przyciągającego
R2 =C2 −F2 - skierowana jest od ciała przyciągającego
Precesja ma charakter zmiany wiekowej i dzieli się na:
1. księżycowo-słoneczną – powodującą zmianę położenia punktu równonocy
na ekliptyce
2. planetarną – powodująca zmianę położenia ekliptyki
Wpływ precesji na położenie punktu równonocy i równika przedstawiony jest na
rysunku
P1 – precesja księżycowo-słoneczna
q1 – precesja planetarna
p – całkowita precesja w długości
m – całkowita precesja w rektascensji
n – całkowita precesja w deklinacji
Wzory przybliżone
Zapewniające dokładność obliczeń wpływu precesji dla gwiazd których δ < 80 o
(wzory ścisłe zostaną zaprezentowane w kursie geodezji satelitarnej)
1d α
dα
2
αt − α0 =
(t − t 0 ) + 2 (t − t 0 ) + ...
2 dt 0
dt 0
1 d 2δ
dδ
δ t − δ 0 = (t − t 0 ) + 2 (t − t 0 )2 + ...
2 dt 0
dt 0
dα
= m + n sin α tan δ
dt
2
dδ
= n cos α
dt
W 2006 roku m = 46”1261
n = 20”0425
NUTACJA
Okresowa zmiana położenia równika i punktu równonocy wywołana przez
siły wywołujące precesję. Nutacja składa się z sumy drgań harmonicznych z
których podstawowy mam okres 18,6 roku.
a = 9.2”
b = 6.9”
a
b
droga bieguna
praw dz iw ego
dro ga biegun a śred nie go
w r u chu p re ce sy jnym
Wpływ nutacji na położenie równika i punktu równonocy
ϒ0 - punkt równonocy w epoce
początkowej
ϒT - punkt równonocy w epoce T
ε0 - nachylenie równika do ekliptyki w
epoce początkowej
εT - nachylenie równika do ekliptyki w
epoce T
∆ε - długookresowa nutacja w nachyleniu
dε - krótkookresowa nutacja w nachyleniu
∆ψ - długookresowa nutacja w długości
dψ - krótkookresowa nutacja w długości
Wartości ∆ψ, dψ, ∆ε i dε oblicza się ze wzorów:
∆ψ + dψ = Nψ i sin Arg i
∆ε + dε = N ε i cos Arg i
gdzie:
Nψ i - amplituda i-tej składowej nutacji w długości
N ε i - amplituda i –tej składowej nutacji w nachyleniu
Dla uzyskania dokładności 0”01 musimy użyć rozwinięcia nutacji rzędu ponad 200.
Główne wyrazy nutacji:
∆ψ = −17"2 sin I − 1"3 sin 2 L + 0"8 sin 2I + ...
dψ = −0"2 sin 2 + ...
∆ε = 9"2 cos I + 0"6 cos 2 L − 0"1cos 2I + ...
dε = 0"1cos 2 + ...
gdzie:
I - długość ekliptyczna węzła wstępującego Księżyca (okres zmiany 18,6 roku)
L – długość ekliptyczna Słońca (okres zmiany roku zwrotnikowego)
- długość ekliptyczna Księżyca (okres 27,6 dnia)
Przybliżone wzory wpływu nutacji na współrzędne równikowe
∆α n = (cos ε + sin ε sin α tan δ )(∆ψ + dψ ) − cos α tan δ (∆ε + dε )
∆δ n = sin ε cos α (∆ψ + dψ ) + sin α (∆ε + dε )
Wzory powyższe stosujemy dla gwiazd których δ ≤ 80 o , wzory ścisłe będą podane w
kursie geodezji satelitarnej.
Nachylenie równika do ekliptyki możemy obliczyć ze wzoru:
ε = 84381"448 − 48"8150T − 0,00059T 2 + 0,001813T 3
gdzie:
T – interwał czasu jaki upłynął od epoki J2000 wyrażony w stuleciach juliańskich
T=
JD − JD 2000
36525
JD2000 – data juliańska w momencie 2000 styczeń 1d5 (doby) jest równa
2451545.0 (o dobie juliańskiej w dalszej części wykładu przy kalendarzach)
JD – data juliańska na moment obserwacji, można ją znaleźć w roczniku astronomicznym
Prędkość Ziemi w jej ruchu obrotowym i ruchu bieguna
Podstawowe równanie (patrz kurs fizyki) – zależność pomiędzy momentem
pędu a wektorem prędkości kątowej:
r
r
K = Iω
gdzie:
r
K - wektor momentu pędu w ruchu obrotowym
I - macierz bezwładności
r
ω - wektor prędkości
I11
I12
I13
I = I 21
I 22
I 23
I 31
I 32
I 33
Macierz bezwładności jest macierzą symetryczną.
Elementy na przekątnej – momenty bezwładności
Elementy poza przekątną – momenty dewiacyjne bądź iloczyny bezwładności
Uwaga – można zorientować tak układ współrzędnych aby jego osie pokrywały
się z osią maksymalnego i minimalnego momentu bezwładności, wtedy elementy
poza przekątną są równe zero.
Prawo zachowania momentu pędu
r
dK r
=L
dt
r
gdzie: L - wypadkowy wektor momentu sił zewnętrznych
Analiza dwóch przypadków
1.Pierwszy przypadek
r
L ≠ 0 I = const - ciało sztywne
r
r r
dK
≠ 0 K = K (t ) - jest funkcja czasu
dt
r
r
K = Iω
r
r
ω = ω (t ) - wektor prędkości jest zmienny w czasie a więc może zmieniać kierunek i moduł
zmiany kierunku – precesja i nutacja
zmiany prędkości – zarówno: nieregularne (pochodna ciśnienia
atmosferycznego), okresowe (w wyniku zmian przyciągania ciał niebieskich),
wiekowe (te same które powodują precesję)
2. Drugi przypadek
r
L=0
I = const
czyli ciało sztywne, na które nie działają siły zewnętrzne lub siły te się wzajemnie
równoważą
r
r
dK
= 0 K = const
dt
r
r
r
K = Iω ω = const
gdyby przypadek ten miał miejsce czyli byłby stały w przestrzeni kierunek osi
obrotu i stały moduł (mamy jednak do czynienia z przypadkiem pierwszym)
Równanie Eulera
p
r
ω = q
r
Ciało jest ciałem sztywnym, główne momenty bezwładności pokrywają
się z osiami op, oq i or.
Równanie Eulera ma postać:
dp
+ (C − B )qr = L p
dt
dq
B
+ ( A − C )rp = Lq
dt
dr
C + (B − A) pq = Lr
dt
A
Dla ciała o symetrii obrotowej na które nie
działają siły zewnętrzne lub się
równoważą otrzymamy A = B, L p = Lq = Lr = 0
dp
= ( A − C )qr
A
dt
dq
= (C − A)rp
A
dt
dr
=0
C
dt
Jeżeli A i C są wielkościami niezmiennymi w czasie czyli mamy do czynienia
z ciałami sztywnymi to
r = const = p2 + q2
czyli oś obrotu Ziemi zmienia swoje położenie względem układu współrzędnych
sztywno związanego z Ziemią. Zjawisko to opisał Euler. Znając wartości
momentów bezwładności a właściwie spłaszczenie dynamiczne A−C
A
można obliczyć okres. Wynosi on 303 dni.
Na przełomie XIX i XX wieku Chandler ustalił, że okres ten wynosi 420 dni.
Różnica pomiędzy tymi wielkościami wynika z wpływy elastyczności Ziemi –
teoria Love’a.
Wpływ ruchu bieguna na szerokość geograficzną
P – biegun ziemski umowny
P’ – biegun ziemski chwilowy
ω - oś obrotu Ziemi
ϕ’ – szerokość geograficzna chwilowa
ϕ - szerokość geograficzna odniesiona do umownego
(międzynarodowego) układu współrzędnych ziemskich
Wpływ ruchu bieguna na współrzędne ziemskie
gdzie:
γ - kąt pomiędzy kierunkiem do
bieguna umownego i chwilowego
Γ - kat pomiędzy południkiem
zerowym (Greenwich) a kierunkiem
do bieguna chwilowego
Współrzędne bieguna chwilowego
x = γ sin Γ
y = γ cos Γ
Redukcja współrzędnych i azymutów do bieguna umownego
ϕ − ϕ ' = − x cos λ + y sin λ
λ − λ ' = − cos λ − y sin λ
A − A' = −( x sin λ + y cos λ )sec ϕ
gdzie:
x, y – współrzędne chwilowego bieguna Ziemi dostępne pod adresem
ftp://hpiers.obspm.fr , http://www.iers.org
SYSTEMY CZASU
Czas gwiazdowy
1.Czas gwiazdowy prawdziwy związany jest z ruchem obrotowym Ziemi
def
S v = tEV
EV - prawdziwy punkt równonocy to taki w którego
położeniu uwzględniony jest wpływ precesji i
nutacji
2. Czas gwiazdowy średni odniesiony jest do
średniego położenia punktu równonocy
Em - średni punkt równonocy to taki, w którego
położeniu uwzględniony jst tylko wpływ
precesji
def
S m = tE m
3. zależność pomiędzy czasem gwiazdowym
prawdziwym i średnim – równanie
równonocy
S v − S m = (∆ψ + dψ ) cos ε
∆ ψ , dψ
(patrz wykład dotyczący nutacji)
długo i krótkookresowa nutacja w długości
Czas słoneczny prawdziwy i czas słoneczny średni
Czas słoneczny prawdziwy
Definicja: Czas słoneczny prawdziwy jest równy katowi godzinnemu Słońca
prawdziwego ±12h
def
TV = t
V±12h
- słońce prawdziwe (rzeczywiste Słońce poruszające się po ekliptyce) jest
odwzorowaniem ruchu Ziemi po orbicie zgodnie z prawami Keplera
V
W związku z tym Słońce porusza się po ekliptyce ze zmienną prędkością
kątową. Zmiana dobowa położenia Słońca na równiku zmienia się sezonowo.
a’ – przyrost dobowy kata godzinnego, zmienia się na skutek zmian prędkości kątowej
pozornego ruchu rocznego Słońca oraz wywołana jest nachyleniem równika do
ekliptyki (patrz rysunek)
a – przyrost dobowy długości ekliptycznej Słońca
Czas słoneczny prawdziwy nie jest więc miarą czasu fizycznego, w związku z tym
wprowadzono pojęcie czasu słonecznego średniego
Czas słoneczny średni
Definicja: czas słoneczny średni jest równy kątowi godzinnemu Słońca średniego ±12h
def
Tm = t
m±12h
– Słońce średnie – punkt poruszający się po równiku ze stałą prędkością kątową
równą prędkości kątowej Słońca prawdziwego. Słońce prawdziwe i Słońce średnie
przechodzą w tym samym momencie przez południk niebieski, którego α ≈18h42m,
co odpowiada w przybliżeniu początkowi roku kalendarzowego.
m
Zależność czasu od długości geograficznej
t A − t B = λ A − λB
t B = TB m 12 h
t A = TA m 12 h
t A − t B = TA − TB
TA − TB = λ A − λB
S A − S B = λ A − λB
Długość geograficzną liczymy dodatnio w kierunku wschodnim od umownego
południka zerowego zwanego potocznie południkiem Greenwich
TA = TGR + λ
S A = S GR + λ
Gdzie TGR, SGR – odpowiednio czas słoneczny i gwiazdowy Greenwich
Średni czas słoneczny Greenwich nazywamy czasem uniwersalnym i oznaczamy
symbolem UT lub TU.
Czasy odniesione do południka miejscowego n.p. punktu A nazywamy czasem
miejscowym.
W życiu cywilnym używamy czasów strefowych różniących się od czasu uniwersalnego
o pełną liczbę godzin.
W Polsce w lecie używamy czasu wschodnioeuropejskiego (CWE)
CWE = TU + 2h
W zimie zaś czasu środkowoeuropejskiego (CSE)
CSE = TU +1h
ZALEZNOŚĆ POMIĘDZY CZASEM
SŁONECZNYM ŚREDNIM I CZASEM
GWIAZDOWYM
Wychodząc ze znanych wcześniej zależności mamy:
h
h
S m = α ☼ m +t ☼m = α ☼ m −12 + t ☼ m +12
Ponieważ
Tm = t ☼ m +12
h
Otrzymamy dla Greenwich
h
( S m )GR = α ☼ m −12 + TU
α ☼ m −12h = 6 h 41m50 s 54841 + 8640184 s812866T + 0 s 093104T 2 − 6 s 210 ⋅10−6 T 3
Gdzie: T = JD − JD2000
36525
Wygodniej jest wykonać obliczenia inaczej, obliczając najpierw czas gwiazdowy
Greenwich o 0h czasu uniwersalnego S0.
(
S 0 = α m − 12 h
)
0h TU
Dalsze przeliczenie przedstawione jest na osi liczbowej na górnej części osi
przedstawiona jest skala w jednostkach TU, na dolnej SGR.
(TU)S – czas uniwersalny wyrażony w jednostkach czasu gwiazdowego
(TU)S = TU + µ
µ - 0.0027379093
Zgodnie z rysunkiem napiszemy:
(Sm)GR=(TU)S+S0=S0+(1+µ)TU=S0+µTU+TU
gdzie:
µTU = red.
Schemat obliczania:
Dany jest moment w czasie środkowo-europejskim, obliczyć moment w czasie
gwiazdowym średnim w Warszawie
Czas środkowoeuropejski
Czas uniwersalny
redukcja
Czas uniwersalny w jednostkach czasu
gwiazdowego
Czas gwiazdowy o 0hTU
Średni czas gwiazdowy Greenwich
Długość geograficzna Warszawy
CSE
-1h
TU
+red=µTU
(TU)S
+S0
(Sm)GR
+λW-wa
(Sm)W-wa
Obliczamy ze wzoru lub
bierzemy z rocznika
Przeliczenie czasu gwiazdowego na średni słoneczny
Schemat obliczania:
Średni czas gwiazdowy W-wa
(Sm)W-wa
Długość geograficzna Warszawy
-λW-wa
Średni czas gwiazdowy Greenwich
(Sm)GR
Czas gwiazdowy o 0hTU
-S0
Czas uniwersalny w jednostkach czasu
gwiazdowego
Czas uniwersalny
(TU)S
-red= ν TU
TU
+1h
Czas środkowoeuropejski
CSE
TU=SGR – S0 – ν (SGR – S0) = (TU)S – ν (TU)S
Gdzie: (TU)S = SGR – S0
ν = 0.0027304336...
Zależność pomiędzy czasem słonecznym prawdziwym i czasem
słonecznym średnim – równanie czasu
Ponieważ:
TV = t ☼V ± 12h = S - α ☼V ± 12h
Tm = t ☼m ± 12h = S - α ☼m ± 12h
Odejmując oba równania mamy:
E = TV – Tm = α ☼m - α ☼V
Gdzie E – równanie czasu
Aby obliczyć równanie czasu musimy obliczyć na dany moment rektascensję Słońca
średniego i prawdziwego. Te pierwszą możemy obliczyć ze wzorów podanych wcześniej,
zaś rektascensja Słońca prawdziwego może być obliczona na podstawie równań ruchu
Ziemi wokół Słońca.
Równanie czasu możemy znaleźć w Roczniku Astronomicznym bądź w
przybliżonej postaci:
E=7m7sin(L+78°)+9m5sin2L
Gdzie: L – średnia długość ekliptyczna Słońca
L=0 w momencie gdy Słońce wstępuje w znak Barana, w 2006 roku 20 marca 18h25m UT
W momencie początku wiosny astronomicznej
E=0
Czas uniwersalny a czas fizyczny
Wszystkie przedstawione wcześniej systemy czasów związane są z ruchem
obrotowym Ziemi. Te same siły, które powodują precesję osi obrotu Ziemi
powodują spowalnianie jej ruchu obrotowego, powodując w ciągu roku
skrócenie doby średniej słonecznej o ok. 0.5s. Ponieważ zmiana prędkości
obrotowej Ziemi ma nie tylko charakter wiekowy ale również okresowy i
nieregularny systemy czasu oparte na ruchu obrotowym nie spełniają postulatu
stałości jednostki, dlatego też w 1967 roku zdefiniowano nowa jednostkę czasu
tzw. Sekundę atomową jako podstawową jednostkę w systemie SI.
Definicja:
sekunda atomowa jest trwaniem 9 192 631 770 okresów rezonansowej częstotliwości
przejścia pomiędzy dwoma nadsubtelnymi (F=4, M=0) i (F=3, M=0) poziomami stanu
podstawowego 2S 1/2 atomu cezu 133.
Tak wyskalowana jednostka czasu jest równa 1 sekundzie efemerydalnej a początek
skali jest związany z epoką 1900.0 tego czasu.
Czas atomowy – TAI zastąpił czas efemeryd ET.
Czas efemeryd – ET – zdefiniowano jako 1/31 556 925.9747 części roku
zwrotnikowego epoki 1900.
Jego dystrybucja opierała się początkowo na obserwacjach ruchu orbitalnego
Ziemi, później Księżyca. Początkowo stosowany był jako argument tablic
astronomicznych.
Obecnie zastąpiony został czasem ziemskim dynamicznym TDT.
TDT = TAI +32.184
Używany jest również czas ziemski TT
TT ≡ TDT
Czasy uniwersalne:
1. UT0 (TU0) – czas uniwersalny prawdziwy (odniesiony do rzeczywistego
położenia osi obrotu Ziemi)
2. UT1 (lub TU1) – czas uniwersalny średni (odniesiony do umownego bieguna.)
UT1 = UT0 + ∆λ
∆λ - redukcja do międzynarodowego bieguna umownego, jest funkcją
współrzędnych x,y bieguna chwilowego.
Czas uniwersalny koordynowany UTC (lub TUC)
Jest czasem zbliżonym do czasu uniwersalnego UT1, ale mający jako
jednostkę 1 sekundę czasu TAI, początek jest znany tak aby TAI − UTC < 1s .
Koordynację skał dodaje się przez dodanie tzw. sekundy przestępnej 31
grudnia lub 30czerwca.
Od stycznia 2006 roku różnica ta wynosi
TAI – UTC = 33s
Czas uniwersalny koordynowany jest naszym czasem cywilnym.
Dla wyznaczenia długości geograficznej musimy posługiwać się czasem UT1.
Poprawkę UT1 – UTC można znaleźć w Biuletynie IERS (http://hpiers.obspm.fr)
Czas GPS (GPST)
GPST = TAI – 19s – CO
Gdzie CO – mała poprawka empiryczna rzędu 10ns.
Inne ważne zależności:
W 2006 roku
ET = UT1 + 65s
TDT = UT1 + 65s
ET ≅ TDT
Kalendarze
Pojęcie roku w astronomii związane jest z przejściem Słońca prze wybrany punkt na
sferze niebieskiej. Mamy więc:
1. rok gwiazdowy (syderyczny) – to okres obiegu Słońca po ekliptyce o 360°.
T = 365d256
→
360°
2. rok zwrotnikowy – okres czasu pomiędzy dwoma przejściami Słońca przez
punkt równonocy
T = 365d242
→
360° - precesja = 360° - 50”
Początek rok Bessela α☼ ≅ 18h42m
3. rok anomalistyczny – okres pomiędzy kolejnymi przejściami Ziemi przez
peryhelium
T = 365d260
→
360° + ruch linii apsyd = 360° + 11”
4. Rok smoczy – okres pomiędzy dwoma kolejnymi przejściami Słońca przez
węzeł orbity Księżyca.
T = 346d62
5. Data Juliańska ( XVI w)
JD = 0 w momencie 4713 r p.n.e. 1 stycznia 12hTU
Kalendarz cywilny
1. kalendarz juliański przyjmuje T = 365,25 i lata przestępne co 4 lata (Juliusz Cezar
46 p.n.e.)
2. kalendarz gregoriański (papież Grzegorz XIII 1582 r.) zniesiono lata przestępne z
lat kończących się na pełne setki, przestępne przyjęto tylko te, które dzielą się
przez 400 (np. 1600, 2000, 2400)
Pojęcie miesiąca w astronomii wiąże się z przejściem Księżyca przez ten sam punkt
sfery niebieskiej.
Zjawiska wynikające z ruchu orbitalnego i obrotowego Ziemi i ich wpływ na współrzędne.
Ruch orbitalny i obrotowy Ziemi odbywa się z prędkością, której nie można przyjąć
jako zaniedbywalną w stosunku do prędkości światła, powoduje więc pozorną zmianę
kierunku do obserwowanego ciała niebieskiego. Zjawisko to nazywamy zjawiskiem
aberracji.
Podobne przemieszczenie Ziemi w ruchu orbitalnym jak i obserwatora na skutek ruchu
obrotowego Ziemi powoduje istotne zmiany kierunku do obserwowanego ciała
niebieskiego, wpływ tego zjawiska nosi nazwę wpływu paralaksy.
Aberracja kierunku światła
Zasada zjawiska aberracji przedstawiona jest na rysunku.
O1 – punkt główny obrazowy w momencie
t0
O1’ – punkt główny obrazowy w
momencie t0 + τ
Gdzie:
τ - czas potrzebny na przejście światła
przez lunetę
∆β - przesunięcie aberracyjne
υ - prędkość obserwatora
∆β " =
gdzie:
k=
υ
c
υ
c
ρ"
ρ " sin β = k sin β
- stała aberracji
Rodzaje aberracji:
km
30
⋅ 206265
sek
1.Roczna k =
≅ 20"
km
300000
sek
- wpływ ruchu orbitalnego Ziemi
2. Dobowa k = 0"3 - wpływ ruchu obrotowego Ziemi. Wartość k odnosi się do
obserwatora znajdującego się na równiku.
- Przykład:
Wpływ aberracji rocznej na współrzędne.
1
1
1 &
1
Y cos ε cos α sec δ + X& sin α sec δ
15
C
C 15
1
1
∆δ ab = − Y& cos ε (tan ε cos δ − sin α sin δ ) + X& cos α sin δ
C
C
Lub też:
∆α ab = −
∆α ab = Cc + Dd
∆δ ab = Cc '+ Dd '
1
C = − Y&
c
1
D = X&
c
Gdzie:
C, D – wielkości redukcyjne
C’, d’ – stałe redukcyjne
Pochodne współrzędnych Ziemi (składowe prędkości) dostępne są na serwerze JPL
(Jet Propultion Laboratory – NASA)
1
cos α sec δ
15
1
d = sin α sec δ
15
c=
c' = (tan ε cos δ − sin α sin δ )
d ' = cos α sin δ
Wartość C, D można znaleźć w Roczniku Astronomicznym
Wartość c, d, c’, d’ – można obliczyć znając współrzędne gwiazdy.
Paralaksa dobowa
Jest to zmiana kierunku do ciała niebieskiego wywołana ruchem obserwatora.
Przykład: paralaksa dobowa
sin p
ρ
sin(180o − ω ' )
=
∆
sin p =
p=
ρ
∆
ρ
∆
sin ω '
ρ " sin ω '
p0 =
ρ
∆
ρ"
p = p0 sin ω '
ω = ω '− p
UWAGA!
Wartość paralaksy dobowej horyzontalnej jest
niezaniedbywalna przy obliczaniu pozycji Słońca,
Księżyca i Planet. Można je znaleźć w Roczniku
Astronomicznym
Refrakcja astronomiczna
Jest to załamanie się promienia światła w atmosferze przy przejściu od próżni aż do
warstw powietrza optycznie najbardziej gęstych na powierzchni Ziemi.
z – odległość zenitalna
prawdziwa
z’ – odległość zenitalna
pomierzona
R = z – z’
Gdzie: R – wpływ refrakcji
R = 60"3
B
273
tan z '
⋅
760 273 + t
Gdzie: B – ciśnienie atmosferyczne w mm HG
t – temperatura w stopniach Celsjusza
Wzór daje poprawne wartości powyżej 5 stopni wysokości nad
horyzontem.
Refrakcja w horyzoncie dla średnich szerokości geograficznych
R=35’
Refrakcja w poziomie częstotliwości fal radiowych
W teorii propagacji fal elektromagnetycznych rozpatruje się dwie podstawowe warstwy,
troposferę do wysokości 7-20 km oraz jonosferę. Temperatura powietrza maleje od
powierzchni Ziemi aż do troposfery gdzie osiąga wartość około -55°C. Dalej następuje
inwersja gradientu temperatury aż do stratopauzy na wysokości około 50 km po czym
temperatura ponownie zaczyna maleć aż do mezopauzy, powyżej której mamy jonosferę
czyli warstwę zjonizowanego gazu zawierającego swobodne elektrony uwolnione głównie
przy nadfioletowym promieniowaniu Słońca.
Refrakcja troposferyczna
Troposfera dla częstotliwości niższych od 30GHz jest ośrodkiem dyspersyjnym w
którym refrakcja praktycznie nie zależy od częstotliwości. Wzór na wpływ refrakcji
troposferycznej na odległość (Hopfield) można przedstawić przy pomocy wzoru:
δr =
Kd
sin h 2 + 6.25
+
Kw
sin h 2 + 2,25
Gdzie: h – wysokość satelity nad horyzontem
Kd, Kw – oznaczają odpowiednio parametry obliczane dla suchego i wilgotnego
powietrza, oblicza się je z zależności:
4810e
P
K d = 155,2 ⋅10 −7 H d ; K w = 155,2 ⋅10 −7
Hw
T
T2
Hd=40136+148,72(T-237,16)m
Zaś: P – ciśnienie
Hw=11000m
T - temperatura
Refrakcja jonosferyczna
Silnie zależy zarówno od częstotliwości fali jak i liczby swobodnych elektronów [TEC].
Współczynnika załamania n można przedstawić za pomocą rozwinięcia w szereg
potęgowy:
n = 1+
40.3
[TEC ]
f
Zaś oprócz fali nośnej ∆t otrzymamy dzieląc n przez prędkość światła C
∆t =
40.3
[TEC ]
c⋅ f
Opóźnienie to w kierunku pionowym dla częstotliwości używanych przez system GPS
wynosi do 50 ns, a w horyzoncie może być nawet trzykrotnie większe.










