Przewodnik z prądem w polu
magnetycznym
Na przewodnik
znajdujący się w polu
magnetycznym działa
siła poprzeczna. Jest to
siła Lorentza działająca
na poruszające się
elektrony
przewodnictwa.
Przewodnik z prądem w polu
magnetycznym
Wszystkie elektrony przewodnictwa znajdujące
się w przewodniku o długości L, przejdą przez
płaszczyznę xx’ w czasie
t = L/vd.
Przepływający w tym czasie ładunek jest równy:
q = It = IL/vd
Siła Lorentza:
FB qv B
IL
FB qvB sin 90 vd B sin 90o
vd
FB = ILB
o
Przewodnik z prądem w polu
magnetycznym
Jeżeli pole magnetyczne nie jest
prostopadłe do przewodnika, siła jest
określona jako:
FB IL B
Ramka z prądem w polu
magnetycznym
Na ramkę z prądem znajdującą się w
polu magnetycznym działają siły
magnetyczne F i –F wytwarzające
moment siły, który usiłuje ją obrócić
wokół własnej osi.
Ramka z prądem w polu
magnetycznym
Siła:
F = ILBsinq
widok z góry
widok z boku,
widok z boku
ramka obrócona
FB IL B
Ramka z prądem w polu
magnetycznym
Siła:
F = ILBsinq
Moment siły (zdolność siły F do
wprawiania ciała w ruch obrotowy):
F
b/2
M r F
b/2
M = 2*(b/2)aIBsinq = IabBsinq
F
M
M
Ramka z prądem w polu
magnetycznym
Gdy pojedynczą ramkę zastąpimy cewką składającą się z
N zwojów, moment siły działający na cewkę ma wartość:
M = NIabBsinq
Silnik elektryczny
Praca wykonywana przez silniki elektryczne pochodzi od siły
magnetycznej działającej na przewodnik w polu magnetycznym.
Dipolowy moment
magnetyczny
Moment siły działający na cewkę składającą się z N zwojów
ma wartość:
M = NIabBsinq
Możemy zapisać:
M = mBsinq
lub:
gdzie:
M mB
m = Niab
(moment magnetyczny)
Kierunek m jest zgodny z kierunkiem wektora normalnego n,
prostopadłego do płaszczyzny cewki.
Dipol magnetyczny w polu
magnetycznym
Dipol magnetyczny w zewnętrznym polu magnetycznym ma
magnetyczną energię potencjalną, która zależy od ustawienia
dipola w polu magnetycznym.
Karta magnetyczna
Pasek magnetyczny na karcie magnetycznej zawiera cząsteczki
tlenku żelaza mające swój moment magnetyczny. Poprzez
ustawienie kierunków (góra, dół) momentów magnetycznych,
można zakodować informację w systemie binarnym (0 i 1).
Pasek magnetyczny zawiera 3 ścieżki: 1 i 3 – 210
bitów/cal, 2 – 75 bitów na cal.
Rezonans magnetyczny
MRI + fMRI
MRI
Doświadczenie Oersteda
Przepływ prądu elektrycznego w przewodniku może spowodować
odchylenie igły magnetycznej kompasu.
Pole B wytworzone
przepływem prądu
Wektor dB indukcji magnetycznej pola
wywołanego przepływem prądu wynosi:
m 0 Ids r
dB
4 r 3
prawo Biota Savarta
m0 Ids sin q
dB
4
r2
m0 = 4 10-7 Tm/A – przenikalność magnetyczna próżni
Pole B wytworzone przepływem
prądu w przewodniku
prostoliniowym
Wartość indukcji magnetycznej pola w
odległości R od prostoliniowego przewodnika
wynosi:
m0 I
B
2R
Kierunek wektora B znajdujemy z reguły prawej dłoni: ‘chwytamy’
element prawą ręką, tak aby kciuk wskazywał kierunek prądu. Palce
wskazują kierunek linii pola.
Dwa równoległe przewody z
prądem
Równoległe przewody, w których płyną
prądy, działają na siebie siłami.
Prąd płynący w przewodzie a wytwarza
pole magnetyczne o indukcji:
m0 I a
Ba
2d
Pole Ba działa na przewodnik b siłą
Lorentza:
m 0 LI a I b
Fba I b LBa
2d
Dwa równoległe przewody z
prądem
Kierunek Fba jest zgodny z kierunkiem iloczynu wektorowego Ib x Ba.
Stosując regułę prawej dłoni, stwierdzimy, że przewody, w których
płyną prądy równoległe przyciągają się, a te w których płyną prądy
.anyrównoległe się odpychają
Siła działająca między przewodami, w których płyną prądy
równoległe, jest podstawą definicji Ampera.
1 Amper oznacza natężenie prądu stałego, który płynąc w dwóch
równoległych i prostoliniowych przewodach umieszczonych w
próżni w odległości 1 m, wywołuje między tymi przewodami siłę
o wartości 2*10-7 N, na każdy metr długości przewodu.
Działo szynowe
.
Pociski wystrzeliwane z działa szynowego (prąd 106 A, energia
30 MJ) osiągają predkość 36000 km/h w ciągu 1 ms
(przyśpieszenie 106g).
Działo szynowe
.
Prawo Ampera
Do wyznaczania pola magnetycznego pochodzącego od układu
prądów, można stosować prawo Ampera.
Prawo Gaussa
0 E dS qwewn
Prawo Ampera:
B ds m0 I p
Ip jest całkowitym natężeniem prądu
przecinającym powierzchnię ograniczoną
przez kontur całkowania
Prawo Ampera - przykład
Wyznaczmy pole magnetyczne na zewnątrz przewodu z prądem.
B ds m0 I p
B ds B cos qds B ds B2r
B 2r m0 I
m0 I
B
2r
Ten sam wynik otrzymuje się z prawa Biota- Savarta, lecz
stosując prawo Ampera obliczenia są prostsze.
Ramka w polu magnetycznym
Na ramkę, w której płynie prąd,
znajdującą się w polu magnetycznym
działa moment siły, który usiłuje ją
obrócić wokół własnej osi.
Gdy moment siły zadziała na
przewodzącą ramkę znajdującą się w
polu magnetycznym, w ramce popłynie
prąd.
Dwa doświadczenia
Gdy przesuwamy magnes sztabkowy w
kierunku pętli, w obwodzie popłynie
prąd. Gdy oddalamy magnes, prąd
płynie w kierunku przeciwnym.
Gdy zamkniemy klucz S, w drugim
obwodzie popłynie prąd. Gdy klucz S
otworzymy, w drugim obwodzie
popłynie prąd w kierunku przeciwnym.
Gdy klucz pozostaje zamknięty, prąd w
drugim obwodzie nie płynie.
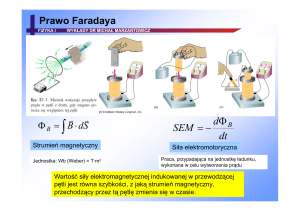
Prawo indukcji Faradaya
W obu doświadczeniach, prąd wytwarzany bez użycia baterii,
był tzw. prądem indukowanym. Płynął on w wyniku pojawiania
się indukowanej siły elektromotorycznej (SEM). Zjawisko
wytwarzania prądu i SEM nazywa się zjawiskiem indukcji
elektromagnetycznej.
Prawo indukcji Faradaya: Wartość SEM indukowanej w
przewodzącej pętli zależy od zmiany liczby sił pola
magnetycznego przechodzących przez pętlę.
Strumień magnetyczny
Strumień prędkości – objętość wody
przepływającej w jednostce czasu przez
powierzchnię.
Strumień pola elektrycznego – ‘ilość pola
elektrycznego’ przechodzącego przez
powierzchnię.
E E dS
Strumień pola magnetycznego – ‘ilość pola
magnetycznego’ przechodzącego przez
powierzchnię.
B B dS
Prawo indukcji Faradaya
Prawo indukcji Faradaya: Wartość SEM E indukowanej w
przewodzącej pętli jest równa szybkości, z jaką strumień
magnetyczny, przechodzących przez pętlę zmienia się w
czasie.
d B
E
dt
Reguła Lenza
Reguła Lenza: Prąd indukowany płynie w takim kierunku,
że pole magnetyczne wytworzone przez ten prąd
przeciwdziała zmianie strumienia magnetycznego, która
ten prąd indukuje.
(„Prąd indukowany przeciwdziała swojej przyczynie”)
Gitara elektryczna
Indukowane pole elektryczne
Pierścień miedziany umieszczony w polu magnetycznym. Gdy
zmieniamy pole magnetyczne, w pierścieniu popłynie prąd
indukowany.
Jeżeli w pierścieniu płynie prąd, to wzdłuż pierścienia musi istnieć
pole elektryczne.
Pole elektryczne jest indukowane nawet wtedy, gdy nie ma
pierścienia miedzianego. Całkowity rozkład pola elektrycznego
można przedstawić za pomocą linii sił pola.
Wniosek: zmienne pole magnetyczne wytwarza pole elektryczne
d B
E ds dt
Potencjał elektryczny
Linie pola elektrycznego wytworzonego przez ładunki statyczne nigdy nie są
zamknięte – zaczynają się na ładunkach dodatnich, a kończą się na ujemnych.
Różnica potencjałów:
Vkonc V pocz
konc
pocz
E ds
Gdy punkt początkowy i końcowy się pokrywa, dostajemy:
E ds 0
ale
E ds 0
Wniosek: potencjał elektryczny można zdefiniować dla pól elektrycznych
wytworzonych ładunki statyczne. Nie można go zdefiniować dla pól elektrycznych
wytworzonych przez indukcję.
Prądnica
Obrót ramki znajdującej się w polu
magnetycznym, indukuje ramce siłę
elektromotoryczną. Przy stałej prędkości
obrotu, SEM będzie miała przebieg
sinusoidalny.
Elementy elektrowni cieplnej (parowej)
1. Chłodnia kominowa
3. Linia transmisyjna (3 fazowa)
4. Transformator
5. Generator elektryczny
6, 9, 11 Turbiny
7 – 14. Silnik parowy
15. Źródło ciepła
Transformator
Transformator składa się z dwóch cewek o różnych
liczbach zwojów, nawiniętych na wspólnym rdzeniu z
żelaza. Uzwojenie pierwotne o liczbie zwojów Np.,
połączone jest ze zmienną siłą SEM. Prąd płynący w
uzwojeniu pierwotnym indukuje zmienny strumień B w
rdzeniu. Strumień B przenika przez uzwojenie wtórne o
liczbie zwojów Nw.
Siła indukowana SEM przypadająca na jeden zwój jest taka sama w obwodzie pierwotnym i wtórnym:
Ez
d B
dt
Napięcie na uzwojeniu pierwotnym: Up= NpEz, napięcie na uzwojeniu wtórnym: Uw= NwEz
Ez
d B U p U w
dt
N p Nw
Uw U p
Nw
Np
transformacja napięcia
Transmisja energii
Moc pobierana energii z elektrowni:
P = UI
Moc rozpraszana na oporze w linii przesyłowej:
P = I2R
U - napięcie w elektrowni, I - prąd w linii przesyłowej, R - opór linii przesyłowej
Załóżmy: U = 735 kV, I = 500 A, R = 220 W
Moc pobierana energii z elektrowni P = (735 *103V)(500 A) = 368 MW
Moc tracona P = (500 A)2(220 W) = 55 MW (15 % mocy dostarczanej)
Załóżmy: U = 735/2 kV, I = 2*500 A, R = 220 W
Moc pobierana energii z elektrowni - bez zmian
Moc tracona P = (1000 A)2(220 W) = 220 MW (63% mocy dostarczanej!)
Wniosek: do przesyłania energii elektrycznej należy stosować jak największe napięcia i
jak najmniejsze natężenia prądu.
System DC
Latarnie zasilane 10 000V, Berlin
1884
Tramwaj zasilany 500V, Frankfurt 1884
National Hotel, Jamestown, California, lata obecne
Nowy Jork, 1890
System AC
Światła miasta, długa przesłona
Prąd trójfazowy
Moc przekazywana w systemie trójfazowym wynosi 1.73UI. Moc
przekazywana przez system jednofazowy wynosi UI. System
trófazowy przenosi 73% mocy, używając 50% kabla.