Pole magnetyczne

Pole magnetyczne
Magnes wytwarza wektorowe pole magnetyczne we
wszystkich punktach otaczającego go przestrzeni.
naładowane elektrycznie cząstki,
poruszające się w przewodniku w
postaci prądu elektrycznego,
wytwarzają pole magnetyczne
cząstki elementarne (np. elektrony)
wytwarzają swoje własne pole
magnetyczne
http://en.wikipedia.org/wiki/Magnet

Definicja wektora B

Wektor E był definiowany jako siła działająca na ładunek:


 F
zatem, wektor B (indukcji magnetycznej) będzie
E
q0
zdefiniowany jako siła działająca na poruszający się
ładunek:
FB
B
F
qv
doświadczenie pokazuje, że równanie
wektorowe można zapisać w postaci:

 
FB  qv  B
B
V
linie pola magnetycznego
różnoimienne bieguny magnetyczne przyciągają się
jednoimienne bieguny magnetyczne się odpychają
magnetyzm Ziemi
Jeden z dowodów istnienia pola magnetycznego
wokół ziemi jest fakt istnienia zorzy polarnych w
okolicach biegunów.
http://www.nasa.gov/mission_pages/themis/auroras/themis_power.html#.Uq4exdLuJyE
Siła magnetyczna działająca na
przewodnik z prądem
L
q  It  I
FB  qvB sin 
v
IL
FB  vB sin 90  ILB
v

 
FB  IL  B
Prawo Biota-Savarta
(rysunki do wzorów)
Prawo Biota-Savarta
Prawo wykryte doświadczalnie opisujące odwrotną proporcjonalność między indukcją magnetyczną B, a odległością r między przewodnikiem a punktem pola.
F
1 qq 1
1 q


Natężenie pola elektrycznego wynosi: E 
2
2
q 4 0 r q 4 0 r
1 dq
zatem, przyczynek: dE 
4 0 r 2

analogią dq dla pola magnetycznego jest Ids (ale to nie skalar):
zatem,
0 Ids sin 
dB 
2
4
r
gdzie, przenikalność magnetyczna próżni
Tm
0  4 10 7
A
0
3


  Ids  r
dB 
4 r
Prawo Ampera
Prawo Ampera jest analogią do prawa Gaussa.
 
 B  ds  0 I
całkowanie wykonujemy po zamkniętym konturze
I jest całkowitym natężeniem prądu przecinającym
powierzchnię ograniczoną przez kontur
przypomnienie: kondensator płaski
natężenie pola elektrycznego
z p. Gaussa:
 
 0  E  dS  qwewn
q   0 ES
różnica potencjałów:

d

0
U   Eds  E  ds  Ed
pamiętając q  CU
otrzymujemy:
C
 0S
d
Prawo indukcji Faradaya
SEM jest indukowana w pętli, gdy zmienia się pole magnetyczne,
przechodzące przez pętlę
lub precyzyjniej, wartość SEM indukowanej w przewodzącej pętli jest
równa szybkości z jaką strumień magnetyczny, przechodzący przez tę
pętlę zmienia się w czasie.
B – strumień magnetyczny:
 
 B   B  dS
gdy


( B  S , B  jednorodne )
prawo Faradaya:
d B
SEM  
dt
 B  BS
Reguła Lenza
Reguła Lenza wynika z zasady zachowania energii i wyznacza
kierunek prądu indukowanego
w
obwodzie.

Zmiana indukcji magnetycznej B w danym obszarze pociąga
 za sobą
powstawanie otaczającego go wirowego pola elektrycznegoE, które ze
swej strony (jeśli to jest możliwe) wzbudza prąd elektryczny
przeciwstawny tejże zmianie.
Prąd indukowany płynie w takim kierunku, że pole magnetyczne
wytworzone przez ten prąd przeciwdziała zmianie strumienia pola
magnetycznego, która ten prąd indukuje.

dB 
B
dt
http://pl.wikipedia.org/wiki/Regu%C5%82a_Lenza
Cewki i indukcyjność
Indukcyjność cewki definiujemy: L  N B
I
N B  (nl )( BS )
B  0 In
N B (nl )( BS ) (nl )(0 In)(S )
L


 0 n 2lS
I
I
I
Zatem indukcyjność na
jednostkę długości
solenoidu w pobliżu jego
środka wynosi:
L
 0 n 2 S
l
N – liczba zwojów
n – liczba zwoją na
jednostkę dł. solenoidu
Samoindukcja
Dwie cewki oddziałują ze sobą. Jeśli w jednej cewce zmienia
się strumień to w cewce obok popłynie prąd. Jednak
indukowana SEM pojawi się także w pierwszej cewce.
Indukowana SEM występuje w cewce , w której natężenie prądu się
zmienia
z def. indukcji
N B  LI
z p. Faradaya SEM  
d ( N B )
dt
zatem, SEM samoindukcji
dI
SEM   L
dt
http://e-fizyka.info/index.php?t=13&id=481&opis=Samoindukcja
Materiały
magnetyczne
diamagnetyki
paramagnetyki
ferromagnetyki
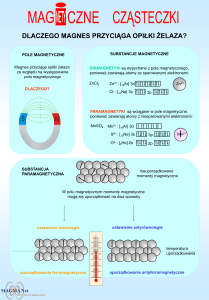
Diamagnetyzm wykazują wszystkie materiały , ale jest to
słabe zjawisko, zaniedbywalne kiedy występują poniższe.
Momenty magnetyczne są indukowane w atomach w
wyniku oddziaływania z zewnętrznym polem
magnetycznym. Wypadkowy moment jest przeciwny do
zewnętrznego pola.
Paramagnetyzm wykazują materiały , których atomy mają
nie zerowy wypadkowy moment magnetyczny.
Momenty magnetyczne atomów w wyniku oddziaływania z
zewnętrznym polem magnetycznym są porządkowane.
Wypadkowy moment jest zgodny z zewnętrznym polem.
Ferromagnetyzm wykazują materiały , których atomy mają
nie zerowy wypadkowy moment magnetyczny i dodatkowo
ten moment jest uporządkowany.
Zewnętrzne pole magnetyczne porządkuje domeny
wytwarzając silne pole magnetyczne, które częściowo
zostaje nawet po ustaniu zewnętrznego pola.
Diamagnetyzm
Diamagnetyzm jest obecny w każdym materiale na podstawie
prawa Faradaya i reguły Lentza.
w materiale diamagnetyczny umieszczony w zewnętrznym polu
magnetycznym powstaje moment magnetyczny skierowany przeciwnie
do pola zewnętrznego,
jeżeli pole zewnętrzne jest niejednorodne to materiał diamagnetyczny
jest wypychany z obszaru silniejszego pola do obszaru pola słabszego
http://www.ru.nl/hfml/research/levitation/diamagnetic/
Paramagnetyzm
Diamagnetyzm dotyczy materiałów z atomowym niezerowym
momentem magnetycznym.
w materiale paramagnetyczny umieszczony w zewnętrznym polu
magnetycznym powstaje moment magnetyczny skierowany zgodnie z
polem zewnętrznym,
jeżeli pole zewnętrzne jest niejednorodne to materiał
paramagnetyczny jest przyciągany do obszaru silniejszego pola
http://www.metasynthesis.com/webbook/16_diradical/diradical.ht
ml
Ferromagnetyzm
Ferromagnetyzm dotyczy materiałów zwanych potocznie
magnesami. Ich trwałe namagnesowanie zanika w
temperaturze Curie (TCurie – dla żelaza: 7700C).
w materiale ferromagnetyczny umieszczony w zewnętrznym polu
magnetycznym powstaje silny moment magnetyczny, skierowany
zgodnie z polem zewnętrznym,
jeżeli pole zewnętrzne jest niejednorodne to materiał
ferromagnetyczny jest przyciągany do obszaru silniejszego pola
http://en.wikipedia.org/wiki/Ferromagnetism