Magnetyzm

MAGNETYZM
Powtórzyć: trygonometrię, kinematykę, dynamikę, energię bryłę sztywną, elektrostatykę, prąd stały.
UWAGA! W FP BRAKUJE ZADAŃ!
Na zewnątrz magnesu linie sił! pola magnetycznego
są skierowane od . . . do . . ., czyli od bieguna . . .
Biegun . . . . . . . . . .,
biegun . . . . . . . . . do . . . . . . . . . , Wewnątrz magnesu – odwrotnie,
czyli od . . . do . . ., więc od bieguna . . . . . do . .
Pole magnetyczne jest polem . . . . . . . . . . . . . . . . ., . . . . . . . . . . . . . . . (nie znaleziono . . . . . . . . . . . . .
Pole elektryczne (np. od ładunku punktowego) jest polem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pole elektryczne wytwarzane przez zmienne pole magnetyczne jest polem . . . . . . . . . . . . . . . . . . . . . . . .
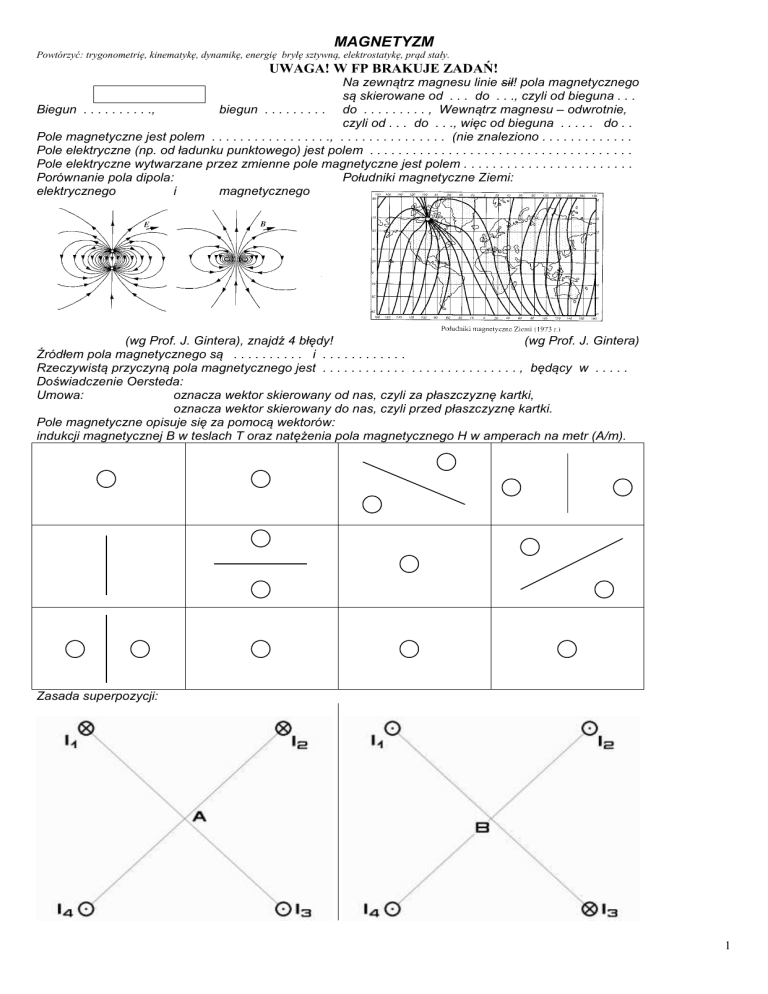
Porównanie pola dipola:
Południki magnetyczne Ziemi:
elektrycznego
i
magnetycznego
(wg Prof. J. Gintera)
(wg Prof. J. Gintera), znajdź 4 błędy!
Źródłem pola magnetycznego są . . . . . . . . . . i . . . . . . . . . . . .
Rzeczywistą przyczyną pola magnetycznego jest . . . . . . . . . . . . . . . . . . . . . . . . . . . , będący w . . . . .
Doświadczenie Oersteda:
Umowa:
oznacza wektor skierowany od nas, czyli za płaszczyznę kartki,
oznacza wektor skierowany do nas, czyli przed płaszczyznę kartki.
Pole magnetyczne opisuje się za pomocą wektorów:
indukcji magnetycznej B w teslach T oraz natężenia pola magnetycznego H w amperach na metr (A/m).
Zasada superpozycji:
1
Siła elektrodynamiczna – to siła działająca ze strony pola . . . . . . . . . o indukcji B na przewód o długości L z prądem I:
. . . . = . . . . . . . .. . .
B = ———
[B] = ——— =
Urządzenie:
. . . . . . . . . . . . . – przetwarza energię . . . . . . . . . . . . . . . na energię . . . . . . . . . . . . . . .
Zwrot siły wyznaczamy . . . . . . . . . . . . . dłonią:
F-.............
B-.............
I–
Siła Lorentza – to siła działająca ze strony pola . . . . . . . . . . . . o . . . . . . . . . . . . . . na poruszającą się z . . . . . . . . . . .
cząstkę o . . . . . . . . . . . .:
F=
Zwrot wyznaczamy z reguły śruby prawoskrętnej, popychając palcami prawej ręki wektor prędkości V w kierunku wektora
indukcji B. Odchylony kciuk pokazuje siłę F, działającą na ładunek dodatni.
2
Siła ta jest . . . . . . . . . . . . . . do prędkości, więc powoduje ruch po . . . . . . . . . . . .
Warunek ruchu:
=
Siła dośrodkowa: FD =
Siła Lorentza: FL =
Kontrola jednostek:
Kontrola jednostek:
Kontrola jednostek:
Kontrola jednostek:
Zadania!
Długość okręgu, po którym z prędkością V porusza się w polu magnetycznym o indukcji B cząstka o masie m i ładunku q
wynosi:
Kontrola jednostek:
Natężenie prądu elektrycznego – prąd elektryczny przypisany cząstce o masie m i ładunku q, poruszającej się w polu
magnetycznym o indukcji B, wynosi:
Kontrola jednostek:
3
Moment pędu, naładowanej ładunkiem q cząstki, poruszającej się po torze kołowym o promieniu R, w polu o indukcji
magnetycznej B wynosi:
Przyspieszenie cząstki o masie m, naładowanej ładunkiem q i poruszającej się z prędkością V w prostopadłym polu
magnetycznym o indukcji B wynosi:
Elektron, będący początkowo w spoczynku, przyspiesza w czasie t w jednorodnym polu elektrycznym o natężeniu E, a
następnie opuszcza to pole i wchodzi w obszar pola magnetycznego jednorodnego o indukcji B i liniach pola,
prostopadłych do kierunku prędkości elektronu. Oblicz promień toru elektronu w polu magnetycznym.
Ruch jednostajny naładowanej cząstki w skrzyżowanych polach: elektrycznym i magnetycznym.
Mając dane natężenie pola elektrycznego E oraz indukcję magnetyczną B, wyznacz prędkość naładowanej cząstki.
Przez otwór w pionowo ustawionej okładce kondensatora płaskiego o pojemności C wlatuje proton z prędkością Vo,
wylatując z drugiej strony wpada w obszar jednorodnego pola magnetycznego, skierowanego poziomo i prostopadłego
do wektora prędkości wylatującego protonu. Na jakiej wysokości H, licząc od otworów uderzy proton w pionową ściankę,
odległą o D od okładek kondensatora, jeśli ładunek na okładce wynosi Q, a odległość między okładkami wynosi d?
Część I - ruch w polu elektrycznym – wyznaczamy prędkość końcową V
Sposób I:
Zasada zachowania energii:
E1 + WNZ = E2
E1 =
WNZ =
(brak . . . . . . . . . . . )
E2 =
Sposób II
Część kinematyczna
Wzór „bez czasu”
Część dynamiczna
Newtona II zasada dynamiki:
Część II – ruch w polu magnetycznym
Równanie okręgu:
Cyklotron – na zmianę współpracują dwa pola:
4
Pole elektryczne przyspiesza
Pole magnetyczne zakrzywia tor
cząstki
Tory naładowanych cząstek w polu magnetycznym.
Jeśli naładowana cząstka wpadnie do pola magnetycznego:
A. równolegle – to porusza się ruchem . . . . . . . . . . . . . . . . . . . . . . . . , bo pole na nią . . . . . . . . . . . .
B. prostopadle – to porusza się ruchem . . . . . . . . . . . . . . . . . . . . . . . . . , patrz siła . . . . . . . . . . . . . .
C. skośnie – to porusza się po . . . . . . . . . . . . . . . . , której:
1. promień zależy od składowej prędkości . . . . . . . . . . . . . do wektora . . . . . . . . . . . . . . . .
2. skok (odległość między zwojami) zależy od składowej prędkości . . . . . . . . . . . . . ( . . . . . . . . .) do wektora . . . . .
...........
Strumień magnetyczny – . . . . . . . . . , określający . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
=
B – . . . . . . . . . . . . . . . . . . . . . . . . . – . . . . . . . . . . . . ., opisujący pole . . . . . . . . . . . . .;
L – . . . . . . . . . . . . . – . . . . . . . . . . . . ., opisujący własności cewki;
i = I – . . . . . . . . . . . . ., . . . . . . . . . . . . . . . . . . . . . . . . . .;
S – pole powierzchni.
Moment magnetyczny – . . . . . . . . . . ., opisujący własności magnetyczne . . . . . . . . . . . . . . . . .
=
I – . . . . . . . . . . . . ., . . . . . . . . . . . . . . . . . . . . . . . . . .;
S – pole powierzchni ramki.
Jeśli ramkę o momencie magnetycznym p m umieścimy w polu o indukcji B, to . . . . . . . . . . . . . . . . . . . .
=
Związek indukcji B z natężeniem pola magnetycznego H
=
B – . . . . . . . . . . . . ., magnetyczna – . . . . . . . . . . . . ., opisujący pole magnetyczne . . . . . . . . . . . . . . . . . .
H – . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . – . . . . . . . . . . . . ., opisujący pole magnetyczne . . .
.......................
– przenikalność magnetyczna bezwzględna danego ośrodka,
– przenikalność magnetyczna bezwzględna próżni,
– przenikalność magnetyczna względna danego ośrodka,
Własności magnetyczne materiałów.
A. Diamagnetyki – r nieco . . . . . . . . . . . od . . . ,
- są lekko . . . . . . . . . . . . . . . . pola magnetycznego,
- . . . . . . . . . . . . . . . . . je nieznacznie,
- ustawiają się . . . . . . . . . . . . . . . . do linii sił! pola magnetycznego (słabo).
np. żywica, woda, szkło, marmur, miedź, bizmut ...
Własności diamagnetyczne są spowodowane . . . . . . . . . . . . . . . . . powłokami elektronowymi (atomy gazów
szlachetnych i jony F -, Cl -, Na +), a także te, które poza wypełnioną powłoką elektronową mają dwa elektrony o spinach .
. . . . . . . . . . . . . . . . . . . . . . . . . np. Zn, Hg, Be, Ca. Dla takich molekuł wypadkowy kręt orbitalny i spinowy jest . . . . . . . .
B. Paramagnetyki – r nieco . . . . . . . . . . . od . . . ,
- są lekko . . . . . . . . . . . . . . . . pola magnetycznego,
- nieznacznie je . . . . . . . . . . . . . . . .,
- ustawiają się . . . . . . . . . . . . . . . . do linii sił! pola magnetycznego (słabo).
np. platyna, aluminium, ebonit, powietrze ...
5
Własności paramagnetyczne posiadają atomy, w których wypadkowy kręt orbitalny lub spinowy jest . . . .
C. Ferromagnetyki – r znacznie . . . . . . . . . . . od . . . ,
- są . . . . . . . . . . . . . . . . . . . . . . . . . pola magnetycznego,
- . . . . . . . . . . . . je . . . . . . . . . . . . . . . .,
- ustawiają się . . . . . . . . . . . . . . . . do linii sił! pola magnetycznego (bardzo mocno).
np. żelazo, nikiel, kobalt, permaloj, hiperm, żeliwo ...
Własności ferromagnetyczne są spowodowane uporządkowaniem . . . . . . . . . . . . . momentów magnetycznych
elektronów atomów pierwiastków, które mają . . . . . . . . . . . . . powłoki wewnętrzne.
Mają histerezę, czyli „pamiętają” w jakim polu ostatnio przebywały.
Histereza
12 – dziewicza, pierwotna krzywa magnesowania
H – rośnie, B – też, lecz nieliniowo,
2 – . . . . . . . . . . ., H . . . ; B = . . . . . . . .,
mimo wzrostu zewnętrznego pola H indukcja B jest
2  3 – H ; B lecz wolniej, podczas . . . . . . . . . .
zewnętrznego pola H indukcja B też . . . . . . . . lecz
3 – H = . . . ., B = . . . - . . . . . . . . . . . . . . . . . . . . .
mimo braku zewnętrznego pola H, w próbce jest . . .
. . . . . . . . . . . - próbka jest trwale namagnesowana.
3  4 – H . . . . , B . . . . – zewnętrzne pole zmieniło zwrot i . .
. . . . . . ., indukcja B . . . . . . . , próbka rozmagnesowuje się.
4 – B = . . . . .; H = . . . . . - . . . . . . . . . . . . . . . magnetyczna, taka wartość zewnętrznego pola H = H K, które powoduje
. . . . . . . . . . . . . . . . . . . . . próbki,
4  5 – H; B,
5 – . . . . . . . . . . . . . . . . . . . – H . . . ., B = . . . . . . . . (patrz . . . . )
5  6 – H . . . . , B . . . . (patrz . . . .  . . . . . )
6 – H = . . . . ; B = . . . . . . - . . . . . . . . . . . . . . . . . . . . . magnetyczna (patrz . . . . )
6  7 – H . . . . 0, B . . . . . (patrz . . . .  . . . . )
7 – H = HK; B = 0 - . . . . . . . . . . . . . . magnetyczna (patrz . . . . )
7  8 – H . . . ., B . . . . . – powtórne magnesowanie.
8 – powtórne . . . . . . . . . . . . . - H . . . ., B = . . . . . . . . . (patrz . . . . )
Pole wewnątrz histerezy jest miarą . . . . . . . . . . . . . zużytej na przemagnesowanie próbki ( . . . . . . . . . . , wydzielającego
się przy przemagnesowaniu) przypadającej na jednostkę objętości.
Dla ferromagnetyków przenikalności  i r zależą
od wartości . . . . . . . . . . . . . . . . .. . . . . . . . . . . .
Jeśli H . . . . to 
a potem . . . . . . . . . . . .
Punkt Curie – temperatura, w której ferromagnetyk staje się . . . . . . . . . . . . . . . . . . . . . . . . . .
Ferromagnetyki dzielą się na:
twarde
Miękkie
Pozostałość magnetyczna
Koercja magnetyczna
Pole wewnątrz histerezy
Zastosowanie:
Magnetostrykcja – zmiana . . . . . . . . . materiału ferromagnetycznego pod wpływem pola . . . . . . . . . . . . .
(„buczenie” transformatora)
Prawo przepływu – prawo Ampera, jest odpowiednikiem prawa . . . . . . . . . . . . . . . . (z elektrostatyki).
Krążenie wektora natężenia pola magnetycznego H wzdłuż krzywej zamkniętej jest równe algebraicznej sumie prądów
zawartych wewnątrz tej krzywej:
Przykłady zastosowań prawa przepływu.
1. Przewodnik prostoliniowy nieskończony
6
Krzywą zamkniętą jest tu . . . . . . . . . . . . . . . . . . . . .
Długość krzywej zamkniętej wynosi więc . . . . . . . . .
Krążenie wektora natężenia pola magnetycznego H
wzdłuż krzywej zamkniętej wynosi więc . . . . . . . . . .
Podstawiamy do prawa Ampera:
Jednostki:
2. Przewodnik kołowy
Bez wyprowadzenia:
H = ––––
Jednostki:
3. Składanie(1) – zastosowanie zasady superpozycji
4. Składanie(2) – zastosowanie zasady superpozycji – dwa prostopadłe przewody prostoliniowe:
7
5. Solenoid, zwojnica, cewka
Krzywą zamkniętą jest tu . . . . . . . . . . .
Natężenie pola magnetycznego (jednorodnego) w solenoidzie, zwojnicy, cewce jest proporcjonalne do
..................................................................................
Jego odpowiednik dla kondensatora to:
Oddziaływanie elektrodynamiczne przewodów z prądem
Natężenie pola magnetycznego wytwarzanego
przez prąd I1 w okolicach przewodu z prądem I2:
Indukcja pola magnetycznego B1, wytwarzanego
przez prąd I1 w okolicach przewodu z prądem I2:
Siła, z jaką przewód pierwszy działa na przewód
drugi:
Jeśli w dwóch sąsiednich przewodach prądy płyną w tym samym kierunku to przewody te . . . . . . . . . . . . Jeśli prądy
płyną w przeciwnych kierunkach (dokładnie – zwrotach) – . . . . . . . . . . . . . . .
Definicja ampera (jednostki natężenia prądu):
Prąd elektryczny ma natężenie jednego ampera, jeśli, płynąc przez dwa równoległe, odległe o 1m prosto-liniowe
przewodniki, o znikomym polu przekroju poprzecznego, powoduje, iż przewodniki te oddziałują na siebie siłą . . . . . . . . . .
. na każdy metr ich długości.
Spirala Rogeta
Jeśli przez zwojnicę, cewkę, solenoid płynie prąd,
to w dwóch sąsiednich zwojach płynie on w . . . . . .
. . . . . . . . . . . . . . . . . . ., więc dwa sąsiednie zwoje
. . . . . . . . . . . . . . . . . . . . . . . , cała cewka dąży do
..........
Prawo Biota – Savarta – Laplace’a jest odpowiednikiem prawa . . . . . . . . . . . . z elektrostatyki,
określa natężenie pola magnetycznego H, wytwarzanego przez element l przewodnika, przez który przepływa stały
prąd I.
Wektorowo:
Skalarnie:
Wniosek
Prawo Biota – Savarta – Laplace’a i Ampera są równoważne. Podobnie jak w elektrostatyce prawo całkowe Gaussa (tu –
Ampera) jest użyteczne przy wysokiej symetrii źródeł pola. Natomiast prawo Coulomba (tu - Prawo Biota – Savarta –
Laplace’a) stosuje się w każdej sytuacji, ale – ponieważ wymaga często żmudnego całkowania, stosujemy je tam, gdzie
niska symetria nie pozwala na zastosowanie praw całkowych.
Indukcyjność własna cewki - . . . . . . . . . . , opisujący własności cewki,
Jego odpowiednik dla kondensatora:
Energia magnetyczna, zgromadzona w rdzeniu cewki:
Jego odpowiednik dla kondensatora:
Gęstość objętościowa energii, zgromadzonej w rdzeniu cewki:
8
MAGNETYZM 2
Indukcja elektromagnetyczna – prawo Faraday’a.
Siła elektromotoryczna indukcji jest proporcjonalna do . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Na wykresie
. . . . . . . . . . . . . . . . od czasu t
. . . . . . . . . . . . . . . . . . . od czasu t
Widać
Jako
Przypomnienie:
Cztery przypadki szczególne:
=
———
=
———
=
———
=
———
= ———— =
= — ———— =
= ———— =
Pierwszy wzór: U =
określa napięcie (dokł. siłę elektromotoryczną SEM),
które pojawia się na . . . . . . . . o długości L, który
z . . . . . . . . . . . . . . . . . porusza się w polu
magnetycznym o . . . . . . . . .
Urządzenie – . . . . . . . . . . . . . . . ,
przetwarza energię . . . . . . . . . . . . . . . . . .
na energię . . . . . . . . . . . . . . . .
Zwrot wyznaczamy . . . . . . . . . . . . . . dłonią:
V- ..................
B-..................
U-..................
9
Ramka porusza się w: prawo
i w lewo:
Drugi wzór:
Ramka obraca się w prawo:
opisuje działanie . . . . . . . . . . . . . . . . . . . . . . . . . .:
Zmienne pole . . . . . . . . . . . . ——— , przechodzące przez rdzeń o stałym polu powierzchni S wytwarza w uzwojeniu
wtórnym zmienną siłę elektromotoryczną (czyli napięcie wtórne transformatora).
Transformator ma:
rdzeń, wykonany z . . . . . . . . . . . . . . . . . . . . . . . . . . . . magnetycznie.
Uzwojenie . . . . . . . . . . . . , które ma
Uzwojenie . . . . . . . . . . . . , które
n1 zwojów, nawiniętych . . . .
ma n2 zwojów, nawiniętych . . . .
drutem, zwojów jest . . . . . więc
drutem, zwojów jest . . . . . . więc
można przyłożyć . . . . . .
. . . . . . . . . . . . . . . . . przemienne
przemienne napięcie . . . ., popłynie
. . . . . . . napięcie . . . ., popłynie
. . . . . prąd . . . . . (też . . . . . . . . . .
. . . . . prąd . . . . . (też . . . . . . .
Prąd I1, płynący w uzwojeniu pierwotnym wytwarza w rdzeniu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..
Transformatory mają . . . . . . . . . . . sprawność – prawie . . . . . %. Wtedy moc dostarczana do uzwojenia . . . . . . . . . . . .
jest prawie równa mocy . . . . . . . . . . przez . . . . . . . . . . . . . . . . . . .:
Przekładnia transformatora:
W transformatorze istnieje zjawisko oddziaływania uzwojenia . . . . . . . . . . . . na . . . . . . . . . . . ., gdy opór
R2, dołączony do uzwojenia . . . . . . . . . . . . . . . . . . . . . . . . to . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., to strumień
magnetyczny w rdzeniu . . . . . . . . . . . ., to . . . . . . . . . . . . . . . . . . ., pobierany ze . . . . . . . . przez . . . . . . . . . . . . . . .
......... – ............
Przesył energii elektrycznej:
Transformator na początku linii przesyłowej energii elektrycznej . . . . . . . . . . . . . . . . . . . . . . . . . . . Dzięki temu przesył –
transport energii elektrycznej na dużej odległości odbywa się przy stosunkowo . . . . . . . . . . . . – daje to . . . . . . . . . . . . .
strat. Straty w linii są proporcjonalne do . . . . . . . . . . . . . . . . . . (zgodnie z wzorem P =. . . . . . ). Jeśli napięcie w linii
przesyłowej zwiększymy dwa razy, to, aby przesłać tę samą moc, prąd przesyłu . . . . . . . . . . . . . . . . . . . . . razy, wtedy
straty . . . . . . . . . . . . . . . . . razy.
Aby transformator pracował poprawnie należy zasilić jego uzwojenie pierwotne napięciem . . . . . . . . . . . .
Jeśli do uzwojenia pierwotnego podłączymy napięcie ze źródła stałego np. bateryjki to obserwujemy indukowanie się
napięcia wtórnego tylko w chwili:
1. . . . . . . . . . . . . . . . . . . . . . . . . . .
2. . . . . . . . . . . . . . . . . . . . . . . . . . .
Gdy źródło napięcia stałego jest dołączone na stałe do uzwojenia pierwotnego transformatora, to w uzwojeniu wtórnym .
. . . . . . . . . . . . . . . . . . . się napięcie, mimo, że w uzwojeniu pierwotnym prąd płynie.
Trzeci wzór U =
=
—— określa napięcie na . . . . . . . . .
Napięcie UL na cewce jest proporcjonalne do szybkości zmian . . . . . . . . . . . . . w cewce.
Jego odpowiednik dla kondensatora:
Prąd, płynący przez kondensator jest proporcjonalny do szybkości zmian . . . . . . . . . . na kondensatorze.
Reguła Lenza („minus” w prawie Faraday’a).
W obwodzie . . . . . . . . . . . . . . . . zwrot SEM (siły elektromotorycznej – w woltach) indukowanej oraz prądu
indukowanego jest taki, że wielkości te . . . . . . . . . . . . . . . . . . zmianom . . . . . . . . . . . . . . . . . .
będącego ich źródłem, a więc . . . . . . . . . . . . . . . strumień, gdy jest w stanie . . . . . . . . . . . . . . .
a . . . . . . . . . . . . . . . . go, gdy jest w stanie . . . . . . . . . . . . . . . . . .
Skoro magnes się . . . . . . . . . ., to cewka chce go
. . . . . . . . . ., więc od strony magnesu indukuje się
biegun . . . Cewka „widziana” jest od strony . . . . .
powiększamy literkę . . . i kończymy ją strzałkami.
Skoro magnes się . . . . . . . . . ., to cewka chce go
. . . . . . . . . ., więc od strony magnesu indukuje się
biegun . . . Cewka „widziana” jest od strony . . . . .
powiększamy literkę . . . i kończymy ją strzałkami.
10
Urządzenie:
Przetwarza
energię:
Wzór:
Ręka:
Przyczyny
główne:
Silnik
Podsumowanie „poruszanych” prętów:
Prądnica
Przyczyny
dodatkowe:
Skutek główny:
Skutek
dodatkowy:
Przykłady:
„ . . .Do pręta o długości L przyłożono napięcie U . . .” – tu chodzi o . . . . . . . . . . . . . . (przyczyną jest
„ . . .Do pręta o długości L przyłożono siłę F . . .” – tu chodzi o . . . . . . . . . . . . . . (przyczyną jest
„ . . .Pręt o długości L rozpędził się do prędkości V . . .” – tu chodzi o . . . . . . . . . . . . . . (przyczyną jest
„ . . .Pręt o długości L rozpędzono do prędkości V . . .” – tu chodzi o . . . . . . . . . . . . . . (przyczyną jest
„ . . .W pręcie o długości L zaindukował się prąd I . . .” – tu chodzi o . . . . . . . . . . . . . . (przyczyną jest
Oblicz maksymalną prędkość pręta, spadającego bez tarcia w prostopadłym polu magnetycznym o indukcji B. Pozostałe
dane: masa i długość pręta, rezystancja, łącząca szyny, przyspieszenie ziemskie.
Dane: m – masa pręta,
Szukane:
VMAX = ?
L – długość pręta,
R – rezystancja, łącząca szyny,
g – przyspieszenie ziemskie,
Rysunek:
Analiza:
Pod wpływem własnego ciężaru pręt zaczyna spadać.
Wtedy jego prędkość jest skierowana w . . . . . . i . . . . . . . .
Jeśli w polu magnetycznym o indukcji . . . . . . . . . . . . . . . . . .
z . . . . . . . . . . . . . . przewód o długości L to . . . . . . . . . . .
................................................
Teraz pręt działa jak . . . . . . . . . . ., więc . . . . . . . . . . .
Napięcie na pręcie jest . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Napięcie na rezystorze jest . . . . . . . . . . . . . . . . . . . . . . . .
Pod wpływem tego . . . . . . . . . . . w obwodzie . . . . . . . . . . .
Jeśli w polu magnetycznym o indukcji . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . przewód o długości L . . . . . . . . . . .
................................................
Teraz pręt działa jak . . . . . . . . . . .
Siła ta . . . . . . . . . . . . . . . . . . . . . . i będzie on . . . . . . . . . . . . . . . . . . . . .
Warunek ruchu jednostajnego – pierwsza zasada dynamiki:
Kontrola jednostek:
Pręt na szynach – FP 435!
11
W jednorodnym polu magnetycznym o indukcji B, na poziomych szynach umieszczono, prostopadły do nich przewodnik o
masie m. Odległość między szynami wynosi L. Po podłączeniu szyn do źródła prądu o SEM E, przewodnik zaczął
przesuwać się z przyspieszeniem a. Współczynnik tarcia przewodu o szyny wynosi . Obliczyć rezystancję wewnętrzną
źródła prądu, jeśli rezystancja zewnętrzna obwodu wynosi R, a przyspieszenie ziemskie – g.
Dane:
Szukana:
B = 1T
rW = ?
m = 100g
L = 3m
E = 2V
a = 0,4m/s2
 = 0,01
R = 100
g = 10m/s2
Równania – prawa Maxwella (w różnych podręcznikach jest różna numeracja!)
I prawo Maxwella – uogólnione prawo Ampera,
II prawo Maxwella – prawo indukcji Faraday’a,
III prawo Maxwella – prawo Gaussa – pole elektryczne,
IV prawo Maxwella – prawo Gaussa – pole magnetyczne.
12