PowerPoint Presentation - LOGIM.EDU.GORZOW.PL :: Strona Główna

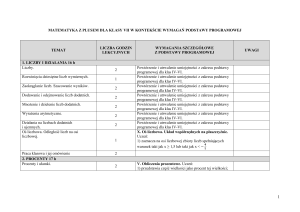
Budowanie i odczytywanie
wyrażeń algebraicznych
Radosław Hołówko
Konsultant: Agnieszka Pożyczka
Budowanie i odczytywanie
wyrażeń algebraicznych





Podział wyrażeń algebraicznych
Jednomiany
Wielomiany
Odczytywanie wyrażeń algebraicznych
Zapisywanie wyrażeń algebraicznych
Podział wyrażeń algebraicznych
Wyrażenia, w których znajdują się liczby,
znaki działań oraz litery nazywamy
wyrażeniami algebraicznymi.
Wyrażenia algebraiczne możemy podzielić
na:
 jednomiany
 wielomiany (sumy algebraiczne)
Jednomiany
Wyrażenia, które są pojedynczymi
liczbami, literami lub iloczynami liczb i
liter, nazywamy jednomianami.
Oto przykłady jednomianów:
3a -x 2a2b3 0,2yz2
Uwaga: Dla uproszczenia zapisu pomija się kropkę
oznaczającą mnożenie przykład
zamiast 3∙a piszemy 3a
Jednomiany
Wszystkie jednomiany staramy się zapisać
w jak najprostszej postaci. W tym celu
porządkujemy czynniki, na przykład:
1
1
2a∙3d∙ 2 a =2∙3∙ 2∙a∙a∙d=3∙a2∙d=3a2d
Czynniki liczbowe zapisujemy na początku
jednomianu, zaś czynniki literowe z reguły w
kolejności alfabetycznej.
Wielomiany
Wielomianami, lub inaczej sumami
algebraicznymi, nazywamy sumy
jednomianów.
Przykłady:
3x+2y
4m-12n
4a2+5b3+c2
Wielomiany
Podobnie jak w przypadku jednomianów,
wielomiany staramy się uporządkować,
przeprowadzając redukcję wyrazów
podobnych (czynniki literowe są takie
same).
Przykład:
4a  5ab  2b  3ba  2b  a 
2
2
2
2
 4a  a  2b  2b  5ab  3ab  5a  2ab
2
2
2
2
2
Odczytywanie wyrażeń
algebraicznych
W celu prawidłowego odczytania
wyrażenia algebraicznego, niezbędna
jest znajomość kolejności wykonywania
działań.
Nazwa danego wyrażenia zależy od
ostatniego wykonanego działania na
nim.
Odczytywanie wyrażeń
algebraicznych
Przykłady odczytywania wyrażeń
algebraicznych:
x+y - suma liczb x i y
2a-b2 - różnica podwojonej liczby a i kwadratu
liczby b
0,5a(b2+c) - iloczyn połowy liczby a i sumy
kwadratu liczby b oraz liczby c
Odczytywanie wyrażeń
algebraicznych
x2
yz
1 1
  
x y
2
- iloraz kwadratu liczby x przez
sumę liczb y i z
- kwadrat różnicy odwrotności liczb
xiy
Zapisywanie wyrażeń
algebraicznych
Czynnością odwrotną do odczytywania
jest zapisywanie wyrażeń
algebraicznych. Oto kilka przykładów:
1.
Różnica sześcianu liczby x i liczby 2
x 2
Odwrotność sumy kwadratu liczby a i
liczby b i liczby c
3
2.
1
a2  b  c
Zapisywanie wyrażeń
algebraicznych
3.
Iloczyn połowy liczby z przez kwadrat sumy
liczb x i y
1
z( x  y)2
2
4.
Iloraz potrojonej sumy liczb a i b przez kwadrat
różnicy liczb a i b
3a  b 
a  b 2
Zapisywanie wyrażeń
algebraicznych
5.
6.
Liczba o 5 większa od liczby a, to:
a+5
Liczba o 5 mniejsza od liczby a, to:
a-5
Zapisywanie wyrażeń
algebraicznych
7.
8.
Liczba 3 razy większa od liczby a, to:
3a
Liczba 3 razy mniejsza od liczby a, to:
1a
3
Warto zobaczyć
A oto linki do stron z dodatkowymi
objaśnieniami:
http://www.scholaris.pl/cms/view_all.php?id=ekran_co_
to_jest_jednomian
http://www.scholaris.pl/cms/index.php/resources/anima
cja_dodawanie+wyraz%C3%B3w+podobnych.html