UH (Bn) - freakone

Karolina Jusiel
18.03.2011r
Pt 13.15
Ćwiczenie nr 57C Wyznaczanie efektu Halla.
1.Efekt Halla
Jeżeli płytkę z metalu lub półprzewodnika włączymy w obwód prądu stałego i umieścimy w
polu magnetycznym, którego wektor indukcji B jest prostopadły do powierzchni płytki i do
kierunku płynącego prądu elektrycznego, to między punktami na bocznych powierzchniach
płytki wytworzy się różnica potencjałów UH, zwana napięciem Halla.
Załóżmy, że nośnikami prądu są elektrony. Jeżeli do płytki przyłożymy napięcie, to w razie
braku pola magnetycznego przez próbkę będzie płynął prąd o natężeniu I. Wytworzone w
próbce pole elektryczne o natężeniu Ex będzie skierowane zgodnie z kierunkiem płynącego
prądu, natomiast elektrony poruszać się będą w kierunku przeciwnym polu z prędkością v x.
Jeżeli teraz pojawi się pole magnetyczne o indukcji B, to na elektrony poruszające się w tym
polu z prędkością vx będzie działać siła Lorentz`a.
FL = -e (vx  B)
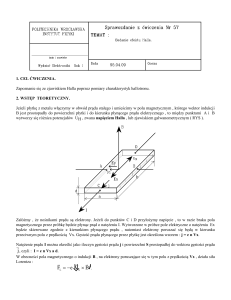
Tak, więc każdy elektron w płytce poruszający się z
prędkością vx, zostaje odchylony od swego początkowego
kierunku ruchu. Wskutek zmiany torów elektrony
gromadzą się na jednej z krawędzi płytki, natomiast na
drugiej wytwarza się niedobór elektronów. Dzięki temu
powstaje dodatkowe pole elektryczne o natężeniu Ey.
Proces gromadzenia się ładunków trwa tak długo, aż powstałe pole poprzeczne E y,
działające na elektrony z siłą
Fy = -eEy
zrównoważy siłę Lorentz`a. Wówczas napięcie Halla obliczamy z równania
UH =  I B,
w którym
1

end
gdzie d - wysokość płytki, n - koncentracja elektronów swobodnych
Mierząc natężenie prądu I płynącego przez płytkę, napięcie Halla UH oraz znając
współczynnik , można wyznaczyć indukcję magnetyczną B. Urządzenie służące do
wyznaczania indukcji magnetycznej, wykorzystujące efekt Halla, nazywa się hallotronem,
współczynnik  zaś czułością hallotronu.
Napięciu Halla towarzyszy niepożądane napięcie asymetrii pierwotnej związane z
poprawnością wykonania elektrod hallowskich. Gdy elektrody te nie leżą dokładnie na
przeciwko siebie wówczas między elektrodami hallowskimi wytwarza się różnica
potencjałów UA zwana napięciem asymetrii pierwotnej, które sumuje się z napięciem Halla i
utrudnia pomiar.
3.Tabela pomiarowa wraz z obliczoną indukcją dla podanych kątów.
Kąt(stopnie)
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
210
220
230
240
250
260
270
280
290
300
310
320
330
340
350
360
U(V)
0,1917
0,1884
0,1829
0,1726
0,1506
0,1312
0,1032
0,0693
0,0393
0,005
-0,033
-0,0689
-0,1032
-0,1256
-0,1547
-0,173
-0,1871
-0,1993
-0,2032
-0,1999
-0,1955
-0,1824
-0,1646
-0,1436
-0,1159
-0,0863
-0,0485
-0,0176
0,0165
0,0595
0,0889
0,1139
0,1419
0,1594
0,176
0,1868
0,1917
Bn
-0,4997
-0,49513
-0,47553
-0,44147
-0,39401
-0,33457
-0,26496
-0,1873
-0,10396
-0,01745
0,069587
0,154508
0,234736
0,307831
0,371572
0,424024
0,463592
0,489074
0,499695
0,495134
0,475528
0,441474
0,394005
0,334565
0,26496
0,187303
0,103956
0,01745
-0,06959
-0,15451
-0,23474
-0,30783
-0,37157
-0,42402
-0,46359
-0,48907
-0,4997
Wykres zależności napięcia Halla od kąta odczytanego z podziałki hallotronu
Natężenie prądu wynosiło 10mA
0.25
0.2
0.15
Napięcie (v)
0.1
0.05
0
-0.05 0
50
100
150
200
250
300
350
400
-0.1
-0.15
-0.2
-0.25
Kąt(stopnie)
Z wykresu można odczytać że wartość αo przy której UH = 0 wynosi około 92o i
272o
Wykres zależności napięcia Halla od wartości składowej
normalnej indukcji Bn = Bo sin (α – αo ) wraz z linią trendu
0.25
0.2
0.15
Napięcie (V)
0.1
-0.6
0.05
0
-0.4
-0.2
-0.05 0
0.2
-0.1
-0.15
-0.2
-0.25
Bn(T)
Używając programu Excel:
Współczynnik kierunkowy prostej opisującej zależności UH (Bn)
Prosta po prawej stronie
a=-0,397±0,0032
0.4
0.6
4. Obliczenia niepewności i obliczenia końcowe:
Dokładność amperomierza
𝑘𝑙 ×𝑍
ΔI=
gdzie:
100
kl-klasa przyrządu=0,5
Z-zakres=15mA
−5
ΔI=7,5× 10
Wyznaczenie czułości hallotronu
gdzie UH oraz B są zmiennymi
𝑈𝐻 = 𝛾𝐼𝑠 𝐵
Stąd:
𝑎 = 𝛾 × 𝐼𝑠
𝑎
𝛾=
𝐼𝑠
γ = 38,8
𝑉
𝐴×𝑇
∆𝛾
∆𝑎
∆𝐼𝑠
= | | + | | = 1,56%
𝛾
𝑎
𝐼𝑠
𝑉
∆𝛾 = 0,6
𝐴×𝑇
Koncentrację elektronów swobodnych
1
𝑛=
𝑒𝛾𝑑
e = 1,6 x 10-19 C
d = 2 μm
Δd/d=5%
n = 8,054 × 1022
1
𝑚3
Niepewność n obliczona metodą różniczki zupełnej
𝜕𝑛
𝜕 1
−1
=
= 2
𝜕𝛾 𝜕𝛾 𝑒𝛾𝑑 𝑒𝛾 𝑑
𝜕𝑛
𝜕 1
−1
=
=
𝜕𝑑 𝜕𝑑 𝑒𝛾𝑑 𝑒𝛾𝑑2
∆𝑛 = |
𝜕𝑛
𝜕𝑛
1
× ∆𝛾| + | × ∆𝑑| = 7,89 × 1020 + 4,03 × 1021 = 4,82 × 1021 3
𝜕𝛾
𝜕𝑑
𝑚
5. Wyniki:
γ=(38,8±0,6)
𝑉
𝐴×𝑇
21
n=(8,054*1022±4,82 × 10 )
Metoda druga:
3.
Napięcie (V)
0
0,2682
0,0961
0,2098
0,1917
0,2293
0,2879
0,2491
0,0174
0,0364
0,0558
0,0755
0,1148
0,1333
0,1528
Natężenie (A)
0
0,014
0,005
0,011
0,01
0,012
0,015
0,013
0,001
0,002
0,003
0,004
0,006
0,007
0,008
4. Korzystając z programu Excel
Współczynnik kierunkowy:
a=19,12
Δa=0,28
Wyznaczenie czułości hallotronu
𝑈𝐻 = 𝛾𝐼𝑠 𝐵
B=0,5T
ΔB=±0,05T
gdzie UH oraz Is są zmiennymi
Stąd:
𝑎 =𝛾×𝐵
𝑎
𝑉
𝛾 = = 38,24
𝐵
𝐴×𝑇
∆𝛾 ∆𝑎 ∆𝐵
=
+
= 11,5%
𝛾
𝑎
𝐵
𝑉
∆𝛾 = ±4,38
𝐴×𝑇
Koncentrację elektronów swobodnych
1
𝑛=
𝑒𝛾𝑑
e = 1,6 x 10-19 C
d = 2 μm
Δd/d=5%
1
𝑛 = 8,172 × 1022 3
m
Niepewność koncentracji elektronów swobodnych obliczona metodą różniczki zupełnej:
∆𝑛 ∆𝑑 ∆𝛾
=
+
= 16,5%
𝑛
𝑑
𝛾
1
∆𝑛 = ±1,35 × 1022 3
𝑚
5.Wyniki:
n=(8,172× 1022 ± 1,35 × 1022 )
𝛾 = (38,24 ± 4,43)
𝑉
𝐴×𝑇
1
𝑚3
6. Wnioski
Wyniki otrzymane dwoma różnymi metodami pokrywają się ze sobą z
uwzględnieniem niepewności pomiarowych. Jednakże koncentracja
elektronów swobodnych i czułość hallotronu obliczona metodą pierwszą daje
dokładniejsze wyniki, obarczone mniejszym błędem.
Wykres zależności napięcia Halla UH od natężenia
prądu IS płynącego przez hallotron wraz z linią
trendu.
0.35
0.3
Napięcie (V)
0.25
0.2
0.15
0.1
0.05
0
0
-0.05
0.002
0.004
0.006
0.008
Natężenie (A)
0.01
0.012
0.014
0.016