Andrzej

Andrzej
Karaś
rok: I
semestr: letni
Wydział
Elektroniki i Telekomunikacji
Politechniki Wrocławskiej
Dr Piotr Sitarek
Ćwiczenie nr:
56-57
Badanie efektu Halla.
Pomiar indukcji magnetycznej
za pomocą fluksometru.
Ocena:
15.03.2000 r.
1. Wstęp teoretyczny.
1.1
Efekt Halla.
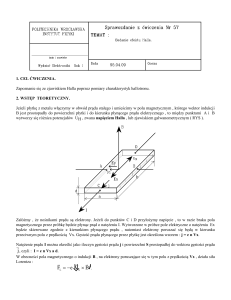
Jeżeli płytkę z metalu lub półprzewodnika włączymy w obwód prądu stałego i umieścimy w polu
magnetycznym, którego wektor indukcji B jest prostopadły do powierzchni płytki i do kierunku
płynącego prądu elektrycznego, to między punktami na bocznych powierzchniach płytki wytworzy się
różnica potencjałów UH, zwana napięciem Halla.
Załóżmy, że nośnikami prądu są elektrony. Jeżeli do płytki przyłożymy napięcie, to w razie braku
pola magnetycznego przez próbkę będzie płynął prąd o natężeniu I. Wytworzone w próbce pole
elektryczne o natężeniu Ex będzie skierowane zgodnie z kierunkiem płynącego prądu, natomiast
elektrony poruszać się będą w kierunku przeciwnym polu z prędkością vx. Jeżeli teraz pojawi się pole
magnetyczne o indukcji B, to na elektrony poruszające się w tym polu z prędkością vx będzie działać siła
Lorentz`a.
FL = -e (vx  B)
Tak, więc każdy elektron w płytce poruszający się z prędkością vx, zostaje odchylony od swego
początkowego kierunku ruchu. Wskutek zmiany torów elektrony gromadzą się na jednej z krawędzi
płytki, natomiast na drugiej wytwarza się niedobór elektronów. Dzięki temu powstaje dodatkowe pole
elektryczne o natężeniu Ey. Proces gromadzenia się ładunków trwa tak długo, aż powstałe pole
poprzeczne Ey, działające na elektrony z siłą
Fy = -eEy
zrównoważy siłę Lorentz`a. Wówczas napięcie Halla obliczamy z równania
UH =  I B,
w którym
1

end
gdzie d - wysokość płytki.
Mierząc natężenie prądu I płynącego przez płytkę, napięcie Halla UH oraz znając współczynnik ,
można wyznaczyć indukcję magnetyczną B. Urządzenie służące do wyznaczania indukcji magnetycznej,
wykorzystujące efekt Halla, nazywa się hallotronem, współczynnik  zaś czułością hallotronu.
Napięciu Halla towarzyszy niepożądane napięcie asymetrii pierwotnej związane z poprawnością
wykonania elektrod hallowskich. Gdy elektrody te nie leżą dokładnie na przeciwko siebie wówczas
między elektrodami hallowskimi wytwarza się różnica potencjałów U A zwana napięciem asymetrii
pierwotnej, które sumuje się z napięciem Halla i utrudnia pomiar.
1.2
Pomiar indukcji magnetycznej za pomocą fluksometru.
Jedną z często stosowanych metod pomiaru pola magnetycznego jest metoda, w której w badanym
polu umieszczamy cewkę pomiarową Cs zwaną sondą bądź czujnikiem, połączoną z galwanometrem
specjalnego typu. W cewce pomiarowej pod wpływem wywołanej przez nas w jakiś sposób zmiany
strumienia magnetycznego powstaje impuls prądu indukcyjnego, powodujący wychylenie
galwanometru. W wykonywanym ćwiczeniu do pomiaru stosowany jest galwanometr pełzny, zwany też
strumieniomierzem bądź fluksometrem. Wychylenie tego galwanometru jest proporcjonalne nie do
natężenia prądu, ale do ładunku, który przepłynął przez uzwojenie cewki w galwanometrze.
Fluksometr jest galwanometrem bez momentu zwrotnego. Gdy nie płynie prąd przez uzwojenie
cewki zajmuje ona dowolne położenie wokół osi obrotu. Do sprowadzenia cewki w dowolne położenie
zerowe służą specjalne urządzenia mechaniczne bądź elektryczne, obracające ruchomy system
fluksometru. Fluksometr pracuje przy małej rezystancji obwodu cewki RG+R, a zatem przy dużym
tłumieniu elektromagnetycznym r2>>r1. Pod wpływem tego dużego tłumienia ruch cewki bywa w
bardzo krótkim czasie zahamowany.
Wychylenie fluksometru jest proporcjonalne do zmiany strumienia magnetycznego, przenikającego
przez uzwojenie cewki pomiarowej. Fluksometry są bezpośrednio wycechowane w jednostkach
strumienia indukcji magnetycznej w weberach [Wb] = [V·s].
2. Przebieg ćwiczenia:
1) Wyznaczenie zależności napięcia Halla od indukcji magnetycznej UH = f (B),
2) Wyznaczenie zależności napięcia Halla od prądu sterującego UH = f (Is),
3) Pomiar indukcji magnetycznej za pomocą fluksometru,
2.1 Wyznaczanie zależności napięcia Halla od indukcji magnetycznej.
2.1.1
Schematy pomiarowe.
W skład układów pomiarowych wchodzą:
- elektromagnes EL-01,
- zasilacz elektromagnesu ZT-980-4,
- miliamperomierz LM-1,
- Hallotron,
- zasilacz ZT980-3,
- miliamperomierz LM-3,
- woltomierz cyfrowy V530.
Układ zasilający hallotron.
Układ zasilający elektromagnes.
2.1.2
Tabele z wynikami pomiarów i obliczeń.
a) Wyznaczanie charakterystyki UH = f (B)
Lp
1.
2.
3.
4.
5.
6.
7.
8.
9.
B
[T]
0,002
0,003
0,004
0,005
0,006
0,007
0,008
0,009
0,01
B
[T]
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
IM
[mA]
30
43
59
74
89
103
118
133
148
IM
[mA]
0,375
0,375
0,375
0,375
0,75
0,75
0,75
0,75
0,75
UH
[ V]
0,0547
0,0797
0,113
0,124
0,171
0,200
0,225
0,255
0,280
UH
[V]
0,001
0,001
0,001
0,001
0,001
0,001
0,001
0,001
0,001


109,4
106,3
113
99,2
114
114,3
112,5
113,3
112
5,01
4,26
4,12
3,53
3,8
3,71
3,59
3,56
3,49
δ
[%]
4,58
4
3,63
3,56
3,33
3,25
3,19
3,14
3,12
n
1020
5,713
5,881
5,531
6,300
5,482
5,469
5,556
5,515
5,580
n
1020
0,547
0,529
0,477
0,539
0,457
0,451
0,455
0,449
0,453
δn
[%]
9,58
9
8,63
8,56
8,33
8,25
8,19
8,14
8,12
b) Wyznaczanie charakterystyki UH = f (IS)
przy stałej indukcji magnetycznej B=0,5 T
Lp.
Is
[mA]
0,0375
0,0375
0,0375
0,0375
0,0375
0,0375
0,0375
0,0375
0,0375
Is
[mA]
1.
2.
3.
4.
5.
6.
7.
8.
9.
1,0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
UH
[V]
0,0592
0,0904
0,118
0,145
0,175
0,203
0,233
0,259
0,288
UH
[V]
0,001
0,001
0,001
0,001
0,001
0,001
0,001
0,001
0,001


118,4
120.5
118
116
116,7
116
116,5
115,1
115,2
8,82
6,76
5,57
4,86
4,46
4,13
3,93
3,71
3,57
δ
[%]
7,44
5,61
4,72
4,19
3,82
3,56
3,37
3,22
3,1
n
1020
5,279
5,185
5,297
5,388
5,357
5,388
5,365
5,429
5,425
n
1020
0,657
0,550
0,515
0,495
0,472
0,461
0,449
0,446
0,439
δn
[%]
12,44
10,61
9,72
9,19
8,82
8,56
8,37
8,22
8,1
Przykładowe obliczenia do powyższych tabel:
- błąd pomiaru natężenia obliczamy ze wzoru:
klasa  zakres 0,5  75

 0,375 - dla pomiarów 1-5 w tabeli a;
100
100
- dla pomiarów 6-10 w tabeli a – zakres = 150;
- dla pomiarów 1-9 w tabeli b – zakres = 7,5.
dokładność licznika V530 wynosi  0,05% wartości mierzonej +0,01% zakresu (10V):
I 
-
ΔUH  0,001V;
-
błąd wartości indukcji magnetycznej obliczamy wykorzystują dane: B/B = 2%
B = 0,02·B = 0,02·0,1 = 0,002 T;
Wyznaczanie czułości hallotronu:

UH
0,0547

 109,4 ;
IS  B 5 10 3  0,1
z różniczki logarytmicznej:
U
d dU H dIS dB
  H  ln   ln U H  ln IS  ln B 




IS  B

UH
IS
B
 U H IS B




UH
IS
B
I = 0,0375 A
 U H IS B 
 0,001 0,0375 0,002 
    
 = 




 109,4  0,0458 109,4  5,01
IS
B 
5
0,1 
 0,0547
 UH
δγ = 4,58%.
Obliczanie koncentracji elektronów oraz błędów pomiaru:
e = 1,6·10-19 C
d = 0,0001 m;
1
1
1
n=


 5,71297989 1020 ;
19
 21
e  d   1,6 10  0,0001109,4 1,7504 10
n
ponieważ
1
dn
de dd d
,
 ln n   ln e  ln d  ln  
  
ed 
n
e
d

de
 0 to:
e
n d 


n
d

d
 5%
d
 d  
5,01 
 5
n  
   n  

  5,713 1020  0,09579  5,713 1020  0,547278 1020
d

100
109
,
4




n = 9,58 %
2.2 Pomiar indukcji magnetycznej za pomocą fluskometru.
2.2.1
Schemat pomiarowy.
W skład układu pomiarowego wchodzą:
- autotransformator,
- elektromagnes,
- prostownik,
- amperomierz – Multimetr G 1007.500,
- fluksometr → kl.=2,5; zakres=10.
Schemat układu do pomiaru pola magnetycznego fluksometrem.
2.2.1
Tabele z wynikami pomiarów i obliczeń.
Wyznaczanie charakterystyki B = f (I) za pomocą fluksometru
Charakterystyka fluksometru:
- n = 40 - liczba zwojów na cewce fluksometru;
- n = 0,5
- S = 4,70 cm2 = 0,00047 m2 - powierzchnia zwoju;
S = 0,04 cm2 = 0,000004 m2.
Lp
1.
2.
3.
4.
5.
6.
7.
8.
I
[A]
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
I
[A]
0,005
0,01
0,015
0,02
0,025
0,03
0,035
0,04

[mWb]
1,2
2,4
3,6
4,7
5,6
6,7
7,4
8,0

[mWb]
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
B
[mT]
63,83
127,66
191,49
250
297,87
356,38
393,62
425,53
B
[mT]
14,64
15,98
17,32
18,55
19,56
20,78
21,57
22,24
B
[%]
22,93
12,52
9,05
7,42
6,56
5,83
5,48
5,22
Przykładowe obliczenia:
- błąd pomiaru natężenia obliczamy ze wzoru:
ΔI=1%·I=0,01·0,5=0,005A.
Obliczanie indukcji pola magnetycznego:

1,2
B

 63,8297mT
n  S 40  0,00047
- błąd pomiaru indukcji pola magnetycznego liczymy z różniczki logarytmicznej:

dB d dn dS
 ln B  ln   ln n  ln S 




n S
B

n
S
;
B  n S



B

n
S
B
Δn = 0,5;
ΔS = 0,000004 m2;
Δ = 0,25 mWb
 0,25 0,5 0,000004 
B  


  63,83  0,229343  63,83  14,63896mT ;
 1,2 40 0,00047 
B = 22,93%.
3. Wnioski:
W pierwszej części ćwiczenia zapoznaliśmy się ze zjawiskiem Halla. Zgodnie z teorią napięcie Halla
w naszych pomiarach jest proporcjonalne do wartości indukcji magnetycznej, a także do wartości prądu
sterującego. Wyznaczone charakterystyki UH=f(B) oraz UH=f(IS) potwierdziły liniowość tych
zależności, co jest zgodne z założeniami teoretycznymi. Współczynnikiem proporcjonalności jest
czułość hallotronu. Wyznaczone czułości hallotronu  w różnych pomiarach mniej więcej pokrywają się.
Oprócz tego czułość ta pozwala wyznaczyć koncentrację elektronów na krawędzi płytki w zależności od
jej rodzaju (chodzi o rozmiary) oraz wartości napięcia Halla, natężenia sterującego i indukcji
magnetycznej. Błędy wyznaczenia czułości w poszczególnych pomiarach wyznaczone były na
podstawie błędów obliczonych metodą różniczki logarytmicznej.
Hallotrony mają szerokie zastosowanie przy pomiarze różnych elektrycznych i nieelektrycznych
wielkości fizycznych, takich jak indukcja magnetyczna, moc, napięcie, iloczyn dwóch dowolnych
wielkości elektrycznych przetworzonych na napięcie itp.
W drugiej części doświadczenia dokonywaliśmy pomiarów strumienia indukcji magnetycznej za
pomocą fluksometru. Zależność indukcji magnetycznej od wartości natężenia prądu jest proporcjonalna,
choć obarczona pewnymi błędami wynikającymi najprawdopodobniej z niedoskonałości sprzętu, a także
krótkiej możliwości odczytu wartości natężenia pola magnetycznego, ponieważ wywołując dość
gwałtowną zmianę pola magnetycznego poprzez odłączenie cewki wytwarzamy impuls prądu
indukcyjnego, który powoduje wychylenie wskazówki fluksometru. Impuls ten jest krótkotrwały, w
związku, z czym wskazówka galwanometru nagle „skacze” do wartości, którą potrzebujemy odczytać,
po czym automatycznie wraca do położenia początkowego. Znacznie utrudnia to pomiar i zwiększa
możliwość wystąpienia błędu przy odczycie, dlatego też charakterystyka, B=f(I) nie jest liniowa, lecz
lekko zakrzywiona.
Jako błąd woltomierza cyfrowego V 530 przyjąłem błąd dyskretyzacji (0,01% zakresu - 10V),
ponieważ jest on znacznie większy od błędu wyliczonego z klasy przyrządu. Pozostałe błędy obliczyłem
na podstawie klasy i zakresu zastosowanych mierników.