Pomiar indukcji magnetycznej za pomocą hallotronu

Politechnika
Białostocka
Wydział Elektryczny
Katedra Elektrotechniki Teoretycznej i Metrologii
Instrukcja do zajęć laboratoryjnych z przedmiotu
POMIARY ELEKTRYCZNE WIELKOŚCI
NIEELEKTRYCZNYCH 2
Kod przedmiotu:
ES2C200011
Ćwiczenie pt.
Pomiar indukcji magnetycznej za pomocą hallotronu
Numer ćwiczenia
WN 12
Opracował:
dr inż. Wojciech Walendziuk
Białystok 2013
Pomiar indukcji magnetycznej za pomocą hallotronu.
1. Wstęp oraz podstawy teoretyczne.
W 1879r. amerykański fizyk E.H. Hall odkrył zjawisko powstawania siły
elektromotorycznej w wyniku odchylania torów nośników prądu w metalu
znajdującego się w polu magnetycznym. Zjawisko to przez wiele lat nie
odgrywało większej roli, aż do momentu rozwoju prac nad materiałami
półprzewodnikowymi. Materiały takie charakteryzują się znacznie większymi
ruchliwościami nośników prądu, przez co zjawisko Halla jest w nich bardziej
zauważalne. Do materiałów półprzewodnikowych, które wykorzystuje się do
budowy czujników hallotronowych zaliczamy: german Ge, krzem Si,
antymonek i arsenek indowy InSb i InAs, arsenofosforek indowy InAsP, selenek
i tellurek rtęciowy HgSe, i HgTe. Od lat sześćdziesiątych stosuje się także
tellurek rtęciowo-kadmowy CdHgTe oraz arsenek kadmowy Cd3As2.
Wspomniana wcześniej nazwa „czujnik hallotonowy” pochodzi od nazwy
anglojęzycznej czujnika wykorzystującego zjawisko Halla, czyli Hall unit, bądź
też Hall generator. Coraz większa popularność czujników hallotronowych
przyczyniła się do powstania polskiej potocznej nazwy znanej do dzisiaj jako
hallotron.
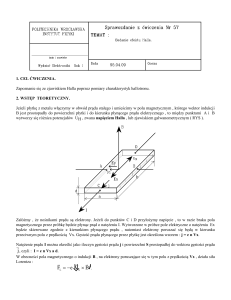
Zasadniczym elementem hallotronu jest prostopadłościenna płytka
półprzewodnikowa lub metalowa. Na krawędziach płytki umieszczone są cztery
elektrody: dwie zasilające i dwie pomiarowe. Elektrody zasilające, (prostopadłe
do osi x) zwane także prądowymi, są odpowiedzialne za przepływ prądu
sterującego Ih. Elektrody pomiarowe umieszczone są na dłuższych krawędziach
płytki i zwane są napięciowymi (Rys.1).
Rys.1. Układ hallotronu umieszczonego w zewnętrznym polu magnetycznym.
Strona 1
Pomiar indukcji magnetycznej za pomocą hallotronu.
Działające na taką płytkę, zewnętrzne pole magnetyczne o indukcji B,
które jest skierowane wzdłuż osi Z, powoduje odchylanie (siła Lorentza wzór 1.)
elektronów tworzących przepływ prądu elektrycznego w metalu lub
półprzewodniku.
Fm  e    B 
(1)
Spowodowany tym nierównomierny rozkład ładunków jest przyczyną
wystąpienia w metalu poprzecznego pola elektrycznego EH skierowanego
wzdłuż ujemnej osi Y, które przeciwstawia się gromadzeniu elektronów w tylnej
części przewodnika.
Rys.2. Ilustracja zjawiska Halla z widocznym poprzecznym polem elektrycznym
EH skierowanym wzdłuż ujemnej osi Y.
Siła elektrostatyczna:
F  e Uh
(2)
działająca na elektrony dzięki zjawisku Halla powinna w stanie równowagi
kompensować siłę magnetyczną tzn:
e U h  e   B
(3)
wprowadzając gęstość prądu:
J  N  e 
(4)
Strona 2
Pomiar indukcji magnetycznej za pomocą hallotronu.
otrzymamy:
e Uh 
J B
N
(5)
gdzie:
N - gęstość odpowiednio elektronów i dziur,
e - ładunek elektronu lub dziury.
Wielkość:
Rh  
U
1
 h
N e
J B
(6)
charakteryzującą właściwości ciała, nazywamy stałą Halla. Wzór taki pozwala
na eksperymentalne wyznaczenie takiej stałej, jak również gęstości wolnych
elektronów N w przewodniku. Znając stałą Halla oraz rezystywność metalu lub
półprzewodnika:
h (H ) 
Uh
J
(7)
można wyznaczyć ruchliwość elektronów μe.
e 
JR
1
 h
Ne U h
(8)
Uwzględniając grubość płytki hallotronu można przyjąć wyrażenie końcowe na
napięcie halla, przedstawione w dogodniejszej postaci jako:
R
Uh  h  Ih  B
d

V  m3 1
V  s V V  s V V 
V



A




2
A

Wb
m
m
Wb
V 

gdzie:
B
I
d
-wartość indukcji magnetycznej
-prąd zasilania Hallotronu
-grubość płytki materiału
Rh
-stała Halla
Strona 3
[104Gs=T]
[A]
[m]
 Vm3
lub
 AWb

Vm 
AT 
(9)
Pomiar indukcji magnetycznej za pomocą hallotronu.
W celu pomiaru zewnętrznej indukcji magnetycznej przy pomocy
czujnika hallotronowego, należy przekształcić wyrażenie (9) do postaci:
B
Uh  d
Rh  I h
(10)
Wprowadzając zmianę kąta przenikania indukcji magnetycznej poprzez
hallotron otrzymujemy zależność:
B
Uh  d
1

Rh  I h sin 
(11)
Chcąc wyznaczyć indukcję cewki cylindrycznej, należy skorzystać z ogólnych
zależności opisujących indukcję magnetyczną oraz natężenie pola
magnetycznego, wytwarzanego przez przewodnik uformowany cylindrycznie i
wiodący prąd o natężeniu I:
BH
(12)
Iz
l
(13)
H
Wynikiem złożenia zależności (12) i (13) jest wzór przedstawiający wartość
indukcji średniej wytworzonej przez cewkę cylindryczną.
Bśr   
Iz
l
(14)
gdzie:
I – prąd zasilający cewkę,
z – liczba zwojów cewki,
l – długość cewki,
μ – jest bezwzględną przenikalnością magnetyczną środowiska wyrażoną
zależnością μ = μ0 μr.
uwzględniając że dla próżni i powietrza μr=1 czyli:
H 
 m 
   0  4   * 10 7 
(15)
Strona 4
Pomiar indukcji magnetycznej za pomocą hallotronu.
indukcję powietrznej cewki cylindrycznej można przedstawić jako:
Bśr  4   * 10 7 
Iz
l
(16)
Należy zwrócić uwagę na fakt, że w przestrzeni objętej zwojami cewki
natężenie pola i indukcja magnetyczna nie są równomierne. Powyższe wzory
należy więc traktować jako przybliżone, gdyż linie magnetyczne w cewce
cylindrycznej przebiegają w sposób przedstawiony na rysunku 3.
Rys.3. Przebieg linii magnetycznych w cewce przedstawione w górnej części
oraz zależności kątów względem osi cewki w dolnej części.
Dość dokładny rezultat otrzymuje się w środkowym punkcie cewki,
oznaczonym symbolem O, bądź po zastosowaniu wzoru:
BK 
0  r  I  z
2l
 cos 1  cos  2 
(17)
w którym wartość indukcji liczona jest dla punktu odniesienia K leżącego w osi
cewki cylindrycznej.
Strona 5
Pomiar indukcji magnetycznej za pomocą hallotronu.
2. Przebieg badań w trakcie zajęć laboratoryjnych.
Celem ćwiczenia jest:
- zapoznanie się z podstawowymi wielkościami charakteryzującymi pole
magnetyczne, takimi jak: indukcja magnetyczna- B, przenikalność
magnetyczna-  ,natężenie pola magnetycznego- H,
- zapoznanie się ze zjawiskiem Halla,
- wykonanie pomiarów indukcji magnetycznej B hallotronem o nieznanych
parametrach technicznych,
- wykorzystanie zjawiska Halla do pomiaru indukcji magnetycznej B oraz
natężenia pola magnetycznego H magnesu trwałego i cewki
cylindrycznej.
Przebieg badań laboratoryjnych:
2.1.
Połączyć układ zasilający hallotron oraz układ pomiarowy według
schematu (Rys.4).
Rys.4. Schemat układu zasilania czujnika Halla.
2.2.
Przeprowadzić kalibrację teslomierza TH-26 oraz wykonać pomiar
wartości indukcji magnesu trwałego, używanego w ćwiczeniu w
punkcie 2.3.
2.3.
Wyznaczyć stałą hallotronu Rh/d = Xh poprzez wykonanie
pomiarów zależności napięcia Halla od prądu zasilającego hallotron
przy stałej indukcji magnetycznej (Rys.5), wyniki umieścić w
tabeli.
Strona 6
Pomiar indukcji magnetycznej za pomocą hallotronu.
Rys.5. Zależność napięcia Halla od prądu sterującego i stałej indukcji
zewnętrznej, dzięki której możliwe jest wyznaczenie stałej hallotronu.
2.4.
Wykonać pomiary napięć Halla w zależności od kąta przenikania
indukcji magnetycznej, przy stałym prądzie zasilającym hallotron
podanym przez prowadzącego (NIE PRZEKRACZAĆ 30mA!!).
2.5.
Dokonać pomiaru indukcji magnetycznej przy pomocy teslomierza
TH-26 i hallotronu dowolnego magnesu trwałego, otrzymanego od
prowadzącego zajęcia laboratoryjne.
2.6.
Wykonać pomiar indukcji magnetycznej cewki powietrznej
podłączonej według schematu (Rys.6), przy pomocy teslomierza i
hallotronu.
Strona 7
Pomiar indukcji magnetycznej za pomocą hallotronu.
3. Opracowanie wyników badań oraz zawartość sprawozdania.
W sprawozdaniu należy umieścić:
 opis przebiegu ćwiczenia,
 wykres zależności napięcia Halla od prądu zasilającego hallotron przy stałej
indukcji magnetycznej,
 wykres zależności napięcia Halla od kąta przenikania indukcji magnetycznej,
przy stałym prądzie zasilającym hallotron,
 wykres zależności indukcji wyliczonej z napięcia Halla od kąta przenikania
zewnętrznej indukcji magnetycznej przy stałym prądzie zasilającym
hallotron,
 wykres błędu względnego indukcji wyliczonej z napięcia Halla w funkcji
kąta przenikania zewnętrznej indukcji magnetycznej magnesu trwałego, przy
stałym prądzie zasilającym hallotron, przy uwzględnieniu, że pomiar
teslomierzem jest pomiarem dokładnym,
 wyniki pomiarów teslomierzem oraz hallotronem magnesu trwałego,
 wyniki pomiarów teslomierzem oraz hallotronem powietrznej cewki
cylindrycznej oraz porównanie ich z wynikami obliczeń teoretycznych,
 wnioski oraz tabele pomiarowe.
4. Pytania sprawdzające
4.1.
4.2.
4.3.
4.4.
4.5.
W jakich jednostkach jest wyrażana indukcja magnetyczna B oraz
natężenie pola magnetycznego H? Jakie są relacje między tymi
wielkościami?
Narysuj oraz opisz elementy najprostszego układu pomiarowego z
czujnikiem Halla, mierzącego natężenie indukcji magnetycznej B.
Opisz procedurę wyznaczania stałej hallotronu.
Wyjaśnij, w jaki sposób wyliczamy wartość indukcji cewki
cylindrycznej.
Znając wykres (Rys.5), wyjaśnij dlaczego: Xh = ΔX / ΔY.
5. Bibliografia
[1] Masewicz T., Paul S.: Podstawy Elektrotechniki dla samouków. PWSZ
Warszawa 1964.
[2] Kobus A., Tuszyński J.: Elektronika, Hallotrony i Gaussotrony. WNT
Warszawa 1966.
[3] Paszkowski B.:Poradnik Inżyniera,Elektronika. WNT Warszawa 1971.
[4] Turowski J.: Elektrodynamika Techniczna. WNT Warszawa 1993.
[5] Masewicz T.: Radioelektronika dla praktyków. WKŁ Warszawa 1986.
Strona 8
Pomiar indukcji magnetycznej za pomocą hallotronu. /* Strona przeznaczona do wykonania kserokopii*/
6. Tabele pomocnicze
2.2
B =..................[mT]
2.3
Tabela 1.
Lp
1
2
3
4
5
6
7
8
9
10
2.3
Ih
Uh
B = const=............….
Xh = Rh/d=.................
1/Xh = d/Rh=................
Tabela 2.
Lp
1
2
3
4
5
6
7
8
9
10
2.5
2.6
=..........................[T]
Kąt α
Magnes trwały:
pomiar teslomierzem
pomiar hallotronem
Cewka cylindryczna:
napięcie zasilania
prąd zasilania
średnia średnica cewki
liczba zwojów
długość cewki
Hallotron:
napięcie Halla
prąd zasilania
Teslomierz:
Uh
B = const =.................
Ih = const =.................
B =.................
B =.................
U =................
I =.................
d =.................
z =.................
l =..................
Uh =................
Ih =.................
B =.................
Data wykonywania ćwiczeń.............................................Podpis prowadzącego...................