Zwiazki_miedzy_funkc..

Materiały pochodzą z Platformy Edukacyjnej
Portalu www.szkolnictwo.pl
Wszelkie treści i zasoby edukacyjne publikowane na łamach Portalu www.szkolnictwo.pl mogą być wykorzystywane przez jego Użytkowników wyłącznie
w zakresie własnego użytku osobistego oraz do użytku w szkołach podczas zajęć dydaktycznych. Kopiowanie, wprowadzanie zmian, przesyłanie, publiczne odtwarzanie
i wszelkie wykorzystywanie tych treści do celów komercyjnych jest niedozwolone. Plik można dowolnie modernizować na potrzeby własne oraz do wykorzystania
w szkołach podczas zajęć dydaktycznych.
ZWIĄZKI MIĘDZY
FUNKCJAMI TRYGONOMETRYCZNYMI
TEGO SAMEGO KĄTA
TOŻSAMOŚCI TRYGONOMETRYCZNE
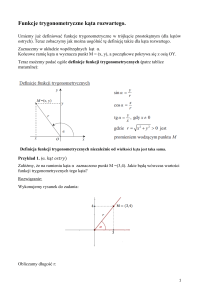
W układzie współrzędnych zaznaczamy kąt ostry, którego ramię końcowe
przechodzi przez punkt P=(x,y). Powstały trójkąt OAP jest prostokątny.
Zapiszemy funkcje trygonometryczne dla kąta POA.
.P
r
y
α
0
x
A
P(x,y)
Wykorzystując powyższe zależności wyprowadzimy wzory – związki między
funkcjami trygonometrycznymi tego samego kąta.
Dodatkowe wzory:
Do zadań potrzebna będzie informacja dotycząca znaków funkcji
trygonometrycznych kątów, znajdujących się w poszczególnych ćwiartkach
układu współrzędnych:
II
I
0
III
IV
Ćw.1. Oblicz wartości funkcji trygonometrycznych
kąta ostrego
jeżeli:
Ćw.2. Oblicz wartości funkcji trygonometrycznych
kąta
jeżeli:
Ćw.3. Oblicz wartości funkcji trygonometrycznych
kąta
jeżeli:
Ćw.4. Oblicz wartości funkcji trygonometrycznych
kąta
jeżeli:
Ćw.5. Oblicz wartości funkcji trygonometrycznych
kąta ostrego
a) P=(-2,4)
którego końcowe ramię przechodzi przez punkt P:
b) P=(5,3)
c) P=(3,-4)
Ćw.6. Uprość wyrażenie:
a)
b)
c)
d)
Ćw.7. Sprawdź, czy prawdziwe są następujące równania
(czy są tożsamością):
a)
Wyrażenie jest tożsamością.
b)
Wyrażenie jest tożsamością.
c)
Wyrażenie jest tożsamością.
d)
Wyrażenie jest tożsamością.
e)
Wyrażenie jest tożsamością.
f)
Wyrażenie jest tożsamością.