TRYGONOMETRIA

TRYGONOMETRIA
Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami
trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie w
związku z zagadnieniami pomiarów na powierzchni Ziemi oraz potrzebami żeglugi morskiej i astronomii.
Określa się cztery 4 funkcje trygonometryczne: sinus (sin), kosinus (cos), tangens (tg), kotangens (ctg)
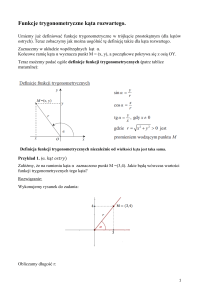
Definicja funkcji trygonometrycznych w
trójkącie prostokątnym.
Funkcje trygonometryczne dla kątów ostrych
można zdefiniować jako stosunki długości
odpowiednich dwóch boków trójkąta
prostokątnego.
,
,
,
Oczywiście znając jedną z wartości funkcji trygonometrycznych i wspierając się twierdzeniem Pitagorasa
można uzyskać wartości pozostałych funkcji. Pomocna w tym będzie równość:
którą łatwo wyprowadzić korzystając z definicji tangensa.
Ponieważ trójkąt jest prostokątny, zachodzi oczywisty związek między kątami
Zatem spełnione są równości:
(
),
(
),
(
i β:
),
(
)
Wartości funkcji dla kątów 30O, 45O, 60O znajdują się w poniższej tabeli.
30O
45O
60O
√
√
√
√
√
1
√
√
1
√
FUNKCJE TRYGONOMETRYCZNE KĄTA SKIEROWANEGO
Kątem skierowanym nazywamy uporządkowaną parę półprostych. Wspólny początek nazywamy
wierzchołkiem kąta skierowanego, pierwszą półprostą nazywamy ramieniem początkowym, drugą
ramieniem końcowym kąta. Dotychczas za jednostkę miary kąta przyjmowaliśmy stopień (1O), czyli
kąta prostego. Dla zdefiniowanego poniżej kąta skierowanego będziemy posługiwać się inną jednostką
miary. Otóż będzie to długość łuku okręgu o promieniu jednostkowym (=1), którą wyznacza dany kąt. I
tak odpowiednio kąt pełny (360O) wyznacza łuk o długości
, kąt półpełny (180O), wyznacza łuk o
długości , kąt prosty (90O), wyznacza łuk o długości , itd.
Obierzmy na płaszczyźnie prostokątny układ współrzędnych OXY. Niech
oznacza dowolny kąt
skierowany, którego ramię początkowe pokrywa się z osią OX, wierzchołek kąta z punktem ( ), ramię
końcowe znajduje się w położeniu dowolnym. Miara kąta skierowanego może być dowolna, gdyż ramię
końcowe możemy obrócić wokół punktu ( ), dowolną ilość razy. Umawiamy się, że obrót w kierunku
przeciwnym do ruchu wskazówek zegara wyznacza kąt dodatni zaś w kierunku przeciwnym, kąt ujemny.
Oczywiście co kąt
ramię końcowe będzie wracać do pierwotnego położenia, co wskazuje że funkcje
trygonometryczne powtarzają swoje wartości co .
Na końcowym ramieniu obierzmy punkt
określa się wzorami:
(
). Funkcje trygonometryczne kąta skierowanego
Ponieważ miara łukowa kąta to dowolna liczba rzeczywista, zamiast będziemy oznaczać ją po prostu .
Patrząc na układ współrzędnych i znaki w odpowiednich ćwiartkach, łatwo wyprowadzamy następujące
(
)
(
)
(
)
zależności:
(
),
,
WYKRESY FUNKCJI TRYGONOMETRYCZNYCH
Na wykresach kąt
został zastąpiony już przez .
Jak widać z wykresów funkcje trygonometryczne są okresowe. W przypadku sinusa i kosinusa okres
wynosi . Tangens powtarza się częściej, co . Wykres funkcji kosinus jest po prostu przesuniętym o
w lewo wykresem funkcji sinus. Ponadto, sinus i kosinus są określone dla wszystkich (także ujemnych:
wartości ujemne odpowiadają obrotowi półprostej w kierunku zgodnym z ruchem wskazówek zegara).
Sinus i kosinus przyjmują wartości z przedziału
. Dwa wykresy z prawej również są do siebie
podobne. Oba to gałęzie rozmieszczone w "pasach" o szerokości . Wykres kotangensa powstaje z
wykresu tangensa poprzez odbicie symetryczne względem osi OY i przesunięcie w prawo o wartość .
Obydwie funkcje w regularnych odstępach są nieokreślone, tangens we wszystkich wielokrotnościach ,
kotangens w nieparzystych wielokrotnościach . I wreszcie tangens i kotangens mogą przyjmować
dowolne wartości (czyli zbiorem wartości tych funkcji jest
).
TOŻSAMOŚCI TRYGONOMETRYCZNE
Tożsamość to równość, która jest zawsze prawdziwa. Najważniejszą z tożsamości trygonometrycznych
jest tzw. jedynka trygonometryczna czyli równość:
Dowód? Spróbujmy zastosować twierdzenie Pitagorasa. Inne tożsamości to np.:
,
,
Oto kilka przykładów dowodzenia tożsamości trygonometrycznych. Pierwsza z nich:
Tożsamość 1)
Przekształcamy lewą stronę równości:
Tożsamość 2)
Przekształcamy lewą stronę równości:
(
Tożsamość 3)
Przekształcamy tym razem prawą stronę.
Tożsamość 4)
(
)
)
ZADANIA
1) Wyznacz długości boków i wartości funkcji trygonometrycznych kątów w trójkącie prostokątnym
, mając dane:
a)
b)
c)
d)
2) Zbuduj kąt ostry
wiedząc, że:
a)
b)
c)
e)
√
√
d)
√
f)
3) Oblicz wartości pozostałych funkcji trygonometrycznych jeśli:
a)
b)
c)
√
d)
√
f)
√
e)
4) Znajdź wartość sinus, kosinus, tangens, kotangens kątów ostrych trójkąta powstałego wskutek
połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.
5) W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8, a kąt ostry 20°. Znajdź
przyprostokątne tego trójkąta.
6) W rombie dany jest bok o długości 10 i kąt ostry
. Oblicz długości przekątnych i pole rombu.
7) W trójkącie równoramiennym długość podstawy wynosi 10, a kąt przy podstawie
promień okręgu opisanego i wpisanego w ten trójkąt.
8) W trójkącie prostokątnym
,
,
kąt przy wierzchołku jest prosty. Wiedząc, że
oblicz
. ( oznacza kąt przy wierzchołku , kąt przy wierzchołku ).
9) Oblicz bez użycia kalkulatora:
a)
b)
c) (
) (
)
10) Doprowadź do najprostszej postaci wyrażenia:
a) (
) (
b) (
)
c) (
) (
)
h)
)
i)
j)
d)
e)
k)
f)
g)
√
. Oblicz
l)
√
11) Wiedząc że kąt jest kątem ostrym i
trygonometrycznych kąta .
12) Wiedząc, że
jest kątem ostrym i
13) Sprawdź tożsamości trygonometryczne:
a)
b) (
) (
c)
d) (
)
e)
f) (
g)
h)
i)
)
)
oblicz wartości pozostałych fukcji
, oblicz