LOGIKA WIELOWARTOSCIOWA

LOGIKA WIELOWARTOŚCIOWA
LOGIKA WIELOWARTOŚCIOWA
12n
0,.1
n1
U podstaw klasycznego rachunku zdań legło założenie o dwuwartościowości wszystkich zdań
w sensie logicznym. Uwolnienie się od tego założenia prowadzi do rachunków zdań
wielowartościowych. I tak np. J. Łukasiewicz wprowadzając trzecią wartość logiczną
zbudował trójwartościowy rachunek zdań Ł3. Podobnie jak on a niezależnie od niego postą
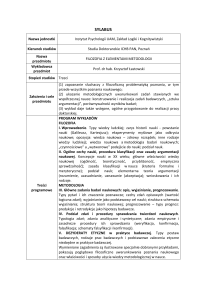
pił E. Post. Jeśli przyjąć, że n oznacza ilość dopuszczalnych wartości logicznych, w systemie
wielowartościowym, to system taki ma następujące wartości:
Dla n = 3 mamy następujące wartości logiczne: 0, ˝, 1
Dla n = 4 mamy zaś: 0, 1/3, 2/3,1
Główna inspiracją zbudowania przez Łukasiewicza logiki trójwartościowej były rozważania
dotyczące determinizmu. Zdania, które dotyczyły przyszłości mogły przyjmować jedną z
trzech wartości logicznych. I tak:
0 - przyjmują te zdania, dla których istnieje obecnie przyczyna wykluczająca ich
zajście;
1- przyjmują te zdania, dla których istnieje obecnie przyczyna powodująca ich zajście
1/2 -przyjmują te zdania, dla których nie istnieje obecnie przyczyna powodująca ich
zajście, ani też przyczyna wykluczająca ich zajście.
Ex.12 Weźmy przykład zdań dotyczących przyszłości i oceńmy je pod względem
wartości logicznych. Niech
p = ”Ziemia będzie kulista”;
q = ” Ziemia będzie nieruchoma”
1
LOGIKA WIELOWARTOŚCIOWA
r = „Ludzie w 2100 r. pobudują osiedla na Marsie”
a) zdanie „p” jest prawdziwe, gdyż istnieje obecnie przyczyna powodująca zajście zdarzenia,
że Ziemia jest kulista
b) zdanie „q” jest fałszywe, gdyż istnieje obecnie przyczyna wykluczająca zajście zdarzenia
że Ziemia jest nieruchoma”
c) r jest niezdeterminowane, czyli posiada wartość 1/2, gdyż nie istnieje obecnie przyczyna
powodująca zajście zdarzenia budowania osiedli przez ludzi na Marsie, ani też przyczyna
wykluczająca zajście takiego zdarzenia.
Podstawową sprawą pozostaje zbudowanie matryc dla zdań złożonych w Ł3.
Oczywiście tabelki charakteryzujące klasyczne operatory są tutaj niewystarczające.
Jednakże Łukasiewicz podając takie charakterystyki zachował dotychczasowe
„zdrowe” intuicje logiczne jakie tkwiły w L, chodzi tu głównie o implikację, która o ile
poprzednik posiada wartość logiczna mniejszą lub równą następnikowi o tyle całe
przyjmuje wartość 1.
Oto główne warunki dla matryc Ł3
Np.=1-p
Apq = max{p, q}
Kpq = min{p, q}
jeśli pq, to Cpq=1
jeśli p>q, to Cpq=1-p+q
Na tej podstawie możemy zbudować matryce dla zdań złożonych w Ł3
1) dla negacji
p
Np
1
0
½
0
½
1
2) dla koniunkcji (Kpq)
q p 1
½
0
1
1
½
0
½
½
½
0
2
LOGIKA WIELOWARTOŚCIOWA
0
0
0
0
3) dla alternatywy (Apq)
q p 1
½
0
1
1
1
1
½
1
½
½
0
1
½
0
4) dla implikacji ( Cpq)
q p 1
½
0
1
1
1
1
½
½
1
1
0
0
½
1
Ex. 13 Zbuduj matrycę dla Epq wiedząc, że Epq=KCpqCqp. Najpierw zbudujemy
dwie matryce dla P = Cpq i Q = Cqp, a następnie dla KPQ
p
q
P
Q
1
1
1
1
1
1
0
0
1
0
0
1
1
0
0
0
0
1
1
1
1
½
½
1
½
½
1
1
½
0
½
1
½
0
½
½
1
KPQ
½
½
½
3
LOGIKA WIELOWARTOŚCIOWA
Wyniki z powyższej matrycy można więc zebrać, i przedstawić podobnie jak dla
pozostałych operatorów logicznych dla Ł3.
q p 1
½
0
1
1
½
0
½
½
1
½
0
0
½
1
Rachunek zdań Ł3 można budować metoda matrycową podobnie jak w przypadku L,
czyli klasycznego rachunku. Zdanie jest tautologia Ł3 gdy przyjmuje wartość 1
(prawdę) . W innych rachunkach wielowartościowych, ze względu na trudności w
interpretacji nowych wartości logicznych nie mówi się o prawdzie, lecz tzw. wartości
wyróżnionej. Dokonano też aksjomatyzacji tego rachunku.
Ex14. Sprawdź, czy zdanie P=” p p „oraz zdanie Q =”(p  p)” są tautologiami
Ł3.
Ex3. Sprawdź, czy zdanie P=” p p „oraz zdanie Q =”(p  p)” są tautologiami Ł3.
a) P= ApNp
p Np
ApNp
1
0
1
0
1
1
½
½
½
b) Q= NKpNp
p Np
KpNp
NKpNp
1
0
0
1
0
1
0
1
4
LOGIKA WIELOWARTOŚCIOWA
½
½
½
½
Logika trójwartościowa Łukasiewicza jest zawarta w logice klasycznej, tzn., że każda
tautologia Ł3 jest tautologią L, lecz nie odwrotnie. Z powyższych matryc widać, że
ważne prawa klasycznego rachunku zdań jak tzw. prawo wyłączonego środka i tzw.
prawo niesprzeczności, posiadające przy tym ciekawe i zgodne z intuicjami
interpretacje, a także długie tradycje w logice nie są tautologiami Ł3.
Szczególnie dużą klasę problemów, dla których systemy wielowartościowe znajdują
zastosowanie stanowią problemy przyrodoznawstwa. Rozumowania bowiem dotyczące
mikroświata prowadzone przy użyciu logiki klasycznej, okazują się rodzić sprzeczności na
gruncie tych teorii, które go dotyczą. . Zauważono bowiem, że własności algebraiczne
operatorów fizyki kwantowej mają charakter inny niż narzuca logika klasyczna. W tym celu
m in. została zbudowana
przez G. Birkhoffa i J. von Neumana tzw. logika kwantowa.
Ciekawe są również analogie między logikami wielowartościowymi a tzw. logikami rozmytymi,
znajdujące zastosowania w komputerowych systemach ekspertowych.
5
LOGIKA WIELOWARTOŚCIOWA
6