Wykład VI

Wykład VI
Twierdzenie o wzajemności
Spadek napięcia i starta mocy w przewodach
zasilających
Dzielnik napięcia, rozszerzanie zakresu
pomiarowego amperomierzy i woltomierzy
Liniowość i nieliniowość obwodu
elektrycznego
Elementy nieliniowe i ich charakterystyki
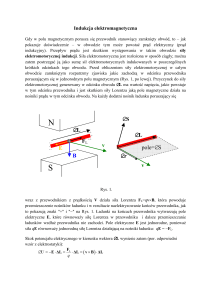
Twierdzenie o wzajemności
Rys. 1. Rysunek objaśniający twierdzenie o wzajemności a) schemat
obwodu elektrycznego z jednym źródłem napięcia i z amperomierzem
w jednej gałęzi b) schemat tego obwodu po zamianie miejsce źródła
napięcia i amperomierza dobór oczek niezależnych
• Jeżeli w dowolną gałąź obwodu liniowego pasywnego włączy się idealne
źródło napięcia stałego E, a w drugą również dowolną gałąź – idealny
amperomierz, to po przełączeniu źródła napięcia i amperomierza
z zachowaniem ich biegunowości wychylenie wskazówki będzie identyczne.
• Prawdziwość twierdzenia można łatwo udowodnić posługując się równaniami
oczkowymi: R11I1  R12 I 2    R1k I k    R1l I l   R1n I n  0 
R21I1  R22 I 2    R2 k I k    R2l I l   R2 n I n  0
............................................................................. 

Rk1 I1  Rk 2 I 2    Rkk I k    Rkl I l   Rkn I n  0 

............................................................................. 
Rl1 I1  Rl 2 I 2    Rlk I k    Rl1 I l   Rln I n  0 

............................................................................. 
Rn1 I1  Rn 2 I 2    Rnk I k    Rnl I l   Rnn I n  0 
• Prąd Il obliczony metodą wyznaczników:
I l   1
k l
Dkl
E
D
• Po przełączeniu źródła napięcia E do gałęzi l układu równań zmienią się tylko
o, tyle, że napięcie źródłowe E wystąpi tylko w wierszu l. Wówczas prąd Ik
wyniesie:
l k D
I k   1
lk
D
E
• Ponieważ podwyznaczniki Dkl i Dlk są sobie równe ze względu na symetrię
wyznacznika charakterystycznego względem przekątnej głównej, musi
zachodzić równość Ik = Il
Spadek napięcia i starta mocy w przewodach
zasilających
•
•
•
Rys. 2. Szkic do objaśnienia spadku napięcia linii prądu stałego a) linia elektryczna b),
c) schemat zastępczy linii
Spadek napięcia U w linii jest równy różnicy napięć na początku i na końcu linii lub
określonego odcinka linii.
Rezystancja linii:
2l 2l
Rl    
S S
Procentowy spadek napięcia:
U % 
•
U
100%
U
U % 
Z przepływem prądu przez linię łączy się starta mocy:
P  Pl I 2 
•
200 l
200l
I 
I
SU
SU
2l 2
I
S
Strata mocy w linii jest równa iloczynowi rezystancji linii i kwadratu prądu w linii.
Dzielnik napięcia, rozszerzanie zakresu pomiarowego
amperomierzy i woltomierzy
•
•
Jeżeli napięcie źródła zasilającego jest za
wysokie do bezpośredniego zasilania odbiornika,
stosuje się tzw. dzielnik napięcia.
Szeregowe i równoległe łączenie oporników
znajduje
w
miernictwie
elektrycznym
zastosowanie również w układach służących do
rozszerzania zakresu pomiarowego woltomierzy
i amperomierzy.
U d ,0 
U
R1

U
R2 R1  R2
1
R1
Rs  (n  1) RV
•
•
Rs – rezystancja opornika włączanego w szereg
z woltomierzem
RV – rezystancja woltomierza
Rys. 3. Schemat dzielnika napięcia
Rys. 5. Załączenie amperomierza z bocznikiem
a) schemat połączeń b) schemat zastępczy
Rys. 4. Załączenie woltomierza a) z
jednym opornikiem szeregowym b) z
kilkoma opornikami i przełącznikiem
wielozakresowym
Ra
Rb 
n 1
•
•
Rb – rezystancja bocznika
Ra – rezystancja amperomierza
Liniowość i nieliniowość obwodu elektrycznego
•
•
•
•
•
W zależności od odpowiedzi obwodu na różne wymuszenia dzieli się obwody
elektryczne lub gałęzie obwodów elektrycznych na:
a) liniowe, czyli linearne, spełniające zasadę superpozycji;
b) nieliniowe czyli nielinearne, nie spełniające zasady superpozycji.
Zasada superpozycji w układzie fizycznym polega na tym, że odpowiedź układu na
kilka wymuszeń działających jednocześnie jest równa sumie odpowiedzi na
poszczególne wymuszenia działające oddzielnie (do układów fizycznych zalicza się
również obwody elektryczne, gałęzie obwodów elektrycznych, a nawet poszczególne
elementy obwodu).
Obwód elektryczny jest liniowy, gdy wszystkie jego elementy są liniowe.
Obwód zawierający przynajmniej jeden element nieliniowy jest obwodem nieliniowym.
Jeżeli dowolne napięcie U1 doprowadzone do zacisków odbiornika rezystancyjnego
wywołuje w nim prąd I1, a napięcie U2 – prąd I2, to odbiornik jest liniowy, gdy zgodnie
z zasadą superpozycji doprowadzone do jego zacisków napięcie U = U1 +U2 wywoła w
nim prąd I = I1 + I2. Jest to możliwe tylko wtedy, gdy tzn. gdy rezystancja odbiornika R
ma stałą wartość, niezależną od płynącego przezeń prądu.
U1 U 2

I1
I2
Rys. 6. Wykres zależności U = f(I) dla elementu rezystancyjnego liniowego
•
•
Cewka jest elementem liniowym, jeżeli jej indukcyjność nie zależy od płynącego przez
nią prądu. Kondensator jest elementem liniowym, jeżeli jego pojemność nie zależy od
napięcie na jego okładzinach.
Źródło napięcia jest liniowe, jeżeli jego napięcie źródłowe oraz rezystancja
wewnętrzna są niezależne od płynącego przez nie prądu.
Elementy nieliniowe i ich charakterystyki
•
•
•
•
Elementy nieliniowe niesterowane są to takie elementy, które dadzą się opisać za
pomocą jednej charakterystyki U = f (I) lub I = f (U). Należą do nich np. żarówki, diody,
łuk elektryczny itp.
Elementy nieliniowe sterowane, które można opisać za pomocą rodziny charakterystyk
dla różnych wartości parametru czynnika sterującego.
Elementy nieliniowe o charakterystyce symetrycznej odznaczają się symetrią krzywych I
= f (U) bądź U = f (I) względem początku układu, co można zapisać w postaci zależności
I = f (U) = - f (-U) lub U = f (I) = - f (-I)
Rys. 7. Charakterystyki napięciowo – prądowe a) żarówki o żarniku wolframowym
b) lampy żelazo – wodorowej c) elementu rezystancyjnego półprzewodnikowego d)
łuku elektrycznego
•
•
Rezystancja statyczna RS nieliniowego elementu rezystancyjnego jest stosunek
napięcia na jego zaciskach do płynącego przezeń prądu.
Rezystancja dynamiczna Rdyn elementu rezystancyjnego nieliniowego jest to stosunek
elementarnego przyrostu napięcia na jego zaciskach do odpowiadającego mu przyrostu
prądu
U
RS 
I
Rdyn
U dU
 lim

I 0 I
dI
Rys. 8. Wyznaczanie graficzne rezystancji dynamicznej a) przykład rezystancji
dynamicznej dodatniej b) przykład rezystancji dynamicznej ujemnej