Zadanie 3.3

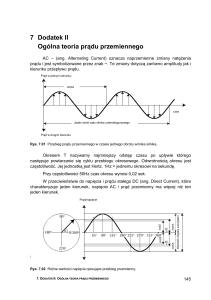
75
3. OBWODY PRĄDU PRZEMIENNEGO JEDNOFAZOWEGO.
Zadanie 3.1.
Cewka indukcyjna zasilana napięciem sinusoidalnym U =100 V o częstotliwości f =
50 Hz pobiera moc P=60 W przy prądzie I =1A. Wyznaczyć rezystancję i indukcyjność
cewki.
Rozwiązanie:
Impedancja cewki wynosi:
Z
U 100

 100 .
I
1
Impedancję Z cewki indukcyjnej traktuje się jako układ rezystancji R i reaktancji X
połączonych szeregowo (rys.3.1.1).
I
R
U
X
Rys. 3.1.1. Schemat zastępczy cewki indukcyjnej.
Prąd pobierany w takim układzie płynie przez oba elementy a impedancja określona jest
zależnością:
Z  R2  X 2 .
Pobierana przez cewkę moc czynna, odpowiadająca wydzielanej przez nią energii cieplnej,
wyraża się wzorem P = I2R.
Zatem rezystancja cewki jest równa
R
P 60

 60  .
I 2 12
Reaktancja cewki wynosi
X  Z 2  R 2  100 2  60 2  80  ,
a jej indukcyjność
L
X


X
80

 0,255 H .
2  f 2  50
Zadanie 3.2.
W układzie jak na rysunku 3.2.1, zasilanym napięciem sinusoidalnym o częstotliwości
f =50 Hz wszystkie woltomierze wskazują napięcie równe 100 V a amperomierz wskazuje
prąd 10 A. Narysować wykres wektorowy i wyznaczyć wartości R , L i C oraz wartość
napięcia zasilającego układ.
76
I
R
L
C
UR
UL
UC
V
V
V
A
U
Rys.3.2.1. Schemat układu do zad.3.2.
Rozwiązanie:
Elementy R , L i C połączone są szeregowo, więc przy sporządzaniu wykresu
wektorowego wygodnie jest zacząć od narysowania wektora prądu I, który płynie przez te
elementy. Kierunek pierwszego rysowanego wektora można przyjąć dowolnie. Na rys.3.2.2
założono I=I, co oznacza że prąd ma tylko składową rzeczywistą, zatem został narysowany
poziomo.
jXL I = U L
UL
RI=UR
UC
I
U
- jXC I = U C
Rys. 3.2.2. Wykres wektorowy do układu z rys.3.2.1.
Pozostałe wektory muszą być rysowane z odpowiednim przesunięciem kątowym równym
przesunięciu fazowemu odpowiadającego im przebiegu. Wektor napięcia na rezystorze UR ma
kierunek taki sam jak prąd I, gdyż ich przebiegi są w fazie. Przebieg napięcia na elemencie
indukcyjnym wyprzedza przebieg prądu o kąt zaś przebieg napięcia na elemencie
pojemnościowym jest opóźniony względem prądu o kąt . Dlatego wektory U L i UC są
przesunięte odpowiednio o kąt +i -względem wektora prądu I.
Napięcie zasilające układ szeregowo połączonych elementów równe jest sumie napięć
na tych elementach. W rozpatrywanym układzie wektory U L i UC znoszą się, toteż wektor
wypadkowy
U = UR + U L + UC = UR.
Wartość napięcia zasilającego jest więc równa:
U = UR= 100 V.
Wartość rezystancji R wyznaczyć można bezpośrednio z wartości napięcia UR i prądu I
77
R
U R 100

 10 .
I
10
Wartości indukcyjności L i pojemności C wynikają z obliczonych reaktancji :
XL
10
U
100

 31,8 mH .
XL  L 
 10 , skąd L 
I
10
2  f 2  50
XC 
U C 100

 10 ,
I
10
skąd C 
1
1

 318 F.
2  f  X C 2  50  10
Zadanie 3.3
Sporządzić wykres wektorowy dla układu pokazanego na rysunku 3.3.1 i na jego
podstawie obliczyć przy jakiej wartości pojemności C prąd pobierany przez układ będzie
najmniejszy. Obliczyć wartość tego prądu. Przyjąć R = 10 , L = 20 mH, U = 100 V, f = 50
Hz.
I
I1
I2
R
C
U
X
Rys. 3.3.1. Schemat układu do zadania 3.3.
Rozwiązanie:
Układ składa się z dwóch gałęzi połączonych równolegle i zasilanych napięciem U. Wykres
wektorowy dla tego układu (rys.3.3.2.) sporządzono przyjmując wektor napięcia zasilającego
jako wektor podstawowy i zakładając, że leży on na osi liczb rzeczywistych (U=U=100V).
I2
I

U
I2
I1
Rys.3.3.2. Wykres wektorowy do układu z rys.3.3.1.
Przy takim założeniu wektor prądu w pierwszej gałęzi wyniesie:
78
I1 
U
100

 (7,18  j 4,49) A,
R  jX L 10  j 6,28
przy czym reaktancja indukcyjna
X L  2  f  L  2  50  20  103  6,28 .
Wektorprądu I2, płynącego przez kondensator wyprzedza wektor U
o kąt
Dodając I2 do wektora I1 otrzymuje się wypadkowy wektor prądu pobieranego przez
układ I. Z wykresu wynika, że przy zadanym prądzie I1, najmniejszą wartość prądu I
uzyskuje się wówczas gdy jest on w fazie z napięciem zasilającym. Obwód jest wtedy w
stanie rezonansu.
Z wykresu można również zauważyć, że moduł prądu I2
odpowiadający
najmniejszemu prądowi I: jest równy składowej urojonej prądu I1. Zatem prąd I2= 4,49A.
Taką wartość prądu uzyskuje się przy reaktancji kondensatora równej:
XC 
U 100

 22,27 .
I 2 4,49
Pojemność kondensatora powinna więc wynosić:
C
1
1

 143 F .
2  f  X C 2  50  22,27
Prąd wypadkowy I jest równy składowej rzeczywistej prądu I1.
I= Re(I1) =7.18 A
Przedstawione rozwiązanie uzyskano na podstawie analizy wykresu wektorowego.
Zadanie można też rozwiązać obliczając impedancję zastępczą i przyrównując jej część
urojoną do zera ( w stanie rezonansu reaktancja zastępcza układu równa jest zero).
Zadanie 3.4.
Obliczyć impedancję zastępczą obwodu pokazanego na rysunku 3.4.1, określić
charakter tej impedancji i obliczyć wypadkowy współczynnik mocy obwodu. Wartości
poszczególnych parametrów obwodu wynoszą: R1 = 4,5 XL1 =2,5 XC1 = 16 R2 = 3
XL2 = 4 XC2= 5 
R1
jXL 1
A
R2
-jXC 2
jXL 2
-jXC 1
B
Rys.3.4.1. Schemat obwodu do zadania 3.4.
79
Rozwiązanie:
Obwód składa się z szeregowo połączonych elementów R1, XL1, Z1 i XC1 (rys.3.4.2), przy
czym Z1 jest impedancją zastępczą dwóch gałęzi równoległych między punktami A i B.
R1
jXL 1
A
Z1
Z
-jXC 1
B
a)
b)
Rys.3.4.2. Przekształcanie obwodu z rys. 3.4.1.
Przy przekształcaniu obwodu prądu przemiennego i redukcji liczby jego elementów
można stosować zależności o takim samym zapisie formalnym jak dla obwodów prądu
stałego z tym, że parametry elementów obwodu muszą być wyrażone za pomocą liczb
zespolonych. Impedancję zastępczą Z1 dwóch gałęzi równoległych między punktami A i B
można zapisać w postaci:
R  jX L 2    jX C 2 
Z 1  R2  jX L 2  //  jX C 2   2
R2  jX L 2    jX C 2 
Po podstawieniu odpowiednich wartości otrzymujemy:
Z1 
3  j 4   j5  (7,5 
3  j 4   j5
j 2,5) A.
Wartość zespolona impedancji zastępczej Z całego obwodu jest równa:
Z  Z1  R1  j X L1  X C1   7,5  j 2,5  4,5  j2,5  16  (12  j16) A
a jej moduł wynosi:
Z  12 2  162  20.
Znak minus przy części urojonej impedancji zastępczej Z wskazuje, że ma ona charakter
pojemnościowy.
Wypadkowy współczynnik mocy obwodu jest równy:
R 12
cos   
 0,6.
Z 20
Zadanie 3.5.
Obliczyć prądy w poszczególnych gałęziach obwodu przedstawionego na rysunku 3.5.1,
sporządzić bilans mocy czynnej i biernej oraz wyznaczyć wypadkowy współczynnik mocy
układu. Narysować wykres wektorowy napięć i prądów w obwodzie. Przyjąć: U = 220V, R1 =
1 R2= 8  R3= 12 XL = 6 , XC = 16 .
80
I
R1
A
I1
R2
I2
R3
U
XL
XC
B
Rys.3.5.1. Schemat układu do zad.3.5.
Rozwiązanie:
Obliczenie prądu pobieranego przez obwód wymaga wyznaczenia jego impedancji zastępczej.
Impedancję tą, przy zastosowaniu metody symbolicznej, można zapisać w postaci:
R  jX L   R3  jX C 
Z  R1  R2  jX L  // R3  jX C   R1  2
R2  jX L   R3  jX C 
Po podstawieniu wartości parametrów otrzymuje się:
8  j6  12  j16  (9,8  j1,6) 
Z 1
8  j6  12  j16
Moduł impedancji zastępczej Z jest zatem równy:
Z = R2  X 2  9,82  1,62  9,93.
Wypadkowy współczynnik mocy układu
cos 
R 9 ,8

 0,987.
Z 9 ,93
Prąd pobierany przez cały układ jest równy
U 220
I 
 22,16A ,
Z 9,93
Zakładając że wektor napięcia zasilającego U ma tylko składową rzeczywistą (U=220V)
można obliczyć zespoloną wartość prądu I:
U
220
I 
 (21,87  j 3,57) A
Z 9,8  j1,6
Napięcie między punktami A i B, wspólne dla dwóch gałęzi obwodu połączonych
równolegle, jest równe różnicy między napięciem zasilającym cały obwód i spadkiem
napięcia na rezystancji R1
U AB  U  I  R1  220  (21,87  j3,57)  1  (198,13  j3,57) V.
Moduł tego napięcia wynosi:
UAB = 198,132  3,57 2  198,16V .
Prądy I1 i I2 są równe:
I1 
U AB
198,13  j3,57

 16,06  j11,6 A,
R2  jX L
8  j6
81
I2 
U AB
198,13  j3,57

 5,8  j8,03 A
R3  jX C
12  j16
zatem ich moduły wynoszą:
I1  16,06 2  11,6 2  19,81 A,
I 2  5,8 2  8,032  9,91 A.
Moc czynna pobierana przez obwód równa jest sumie mocy pobieranych przez występujące w
nim rezystancje a całkowita moc bierna obwodu jest równa algebraicznej sumie mocy
biernych elementów indukcyjnych i elementów pojemnościowych. Zatem w rozpatrywanym
obwodzie:
moc czynna P  I 2 R1  I12 R2  I22 R3  22,162  1  19,822  8  9,912  12  4812W ,
moc bierna Q  I 12 X L  I 22 X C  19,82 2  6  9,912  16  785 var
Uzyskane wartości można sprawdzić obliczając jak wyżej moc całego obwodu - czynną
P=I2R oraz bierną Q= I2X, lub wykorzystując zależność na moc pozorną:
S  P  jQ  U  I   220  (21,87  j3,57)  4812  j 785 VA.
Wykres wektorowy napięć i prądów w obwodzie przedstawiono na rysunku 3.5.2.
I2
U AB

I R1
U
I
I2
I1
Rys.3.5.2. Wykres wektorowy do obwodu z rys. 3.5.1.
Obliczenia prowadzone konsekwentnie metodą symboliczną znacznie ułatwiają narysowanie
wykresu wektorowego, gdyż wartości wszystkich wielkości występujących na tym wykresie
mają formę liczb zespolonych.
Zadanie 3.6.
Cewka indukcyjna pobiera prąd 5 A przy zasilaniu napięciem stałym 50 V lub napięciem
sinusoidalnym 200 V o częstotliwości 50 Hz. Obliczyć częstotliwość napięcia zasilającego
obwód złożony z tej cewki i szeregowo połączonego kondensatora o pojemności 50 F przy
której wystąpi w nim rezonans.
Odpowiedź: f = 64,2 Hz.
Zadanie 3.7.
Obliczyć częstotliwość rezonansową obwodu podanego na rysunku 3.3.1. przyjmując
następujące wartości jego elementów: R = 10 L = 20mH, C = 50F.
82
Odpowiedź: f = 138 Hz.
Zadanie 3.8.
Na sinusoidalne napięcie 1-fazowe U = 220 V załączono równolegle trzy odbiorniki
pobierające następujące prądy i moce czynne: I1 = 12,5 A, P1 = 2,2 kW, I2 = 25 A, P2 = 3,3
kW, I3 = 20 A, P3 = 4,4 kW. Obliczyć prąd pobierany przez układ i wypadkowy
współczynnik mocy.
Odpowiedź: I = 52,7 A, cos