Badanie obwodów prądu przemiennego zawierających elementy R

12
ĆWICZENIE NR 2
BADANIE OBWODÓW PRĄDU PRZEMIENNEGO ZAWIERAJĄCYCH
ELEMENTY R, L, C
2.1. Cel ćwiczenia
Celem ćwiczenia jest poznanie
zawierających elementy R, L, C.
właściwości
obwodów
prądu
przemiennego
2.2. Program ćwiczenia
- pomiary prądów, napięć i mocy w obwodach zawierających elementy R, L, C
a) połączone szeregowo,
b) połączone równolegle,
- wyznaczenie charakterystyki Z=f(f)
2.3. Omówienie programu ćwiczenia
2.3.1 Uwagi ogólne
2.3.1.1. Szeregowe połączenie elementów R, L, C
Podstawowymi elementami odbiornikowymi w obwodach prądu przemiennego są
elementy zawierające rezystancję R (rezystory), indukcyjność L (cewki, dławiki) oraz
pojemność C (kondensatory). Elementy te mogą być połączone szeregowo i równolegle.
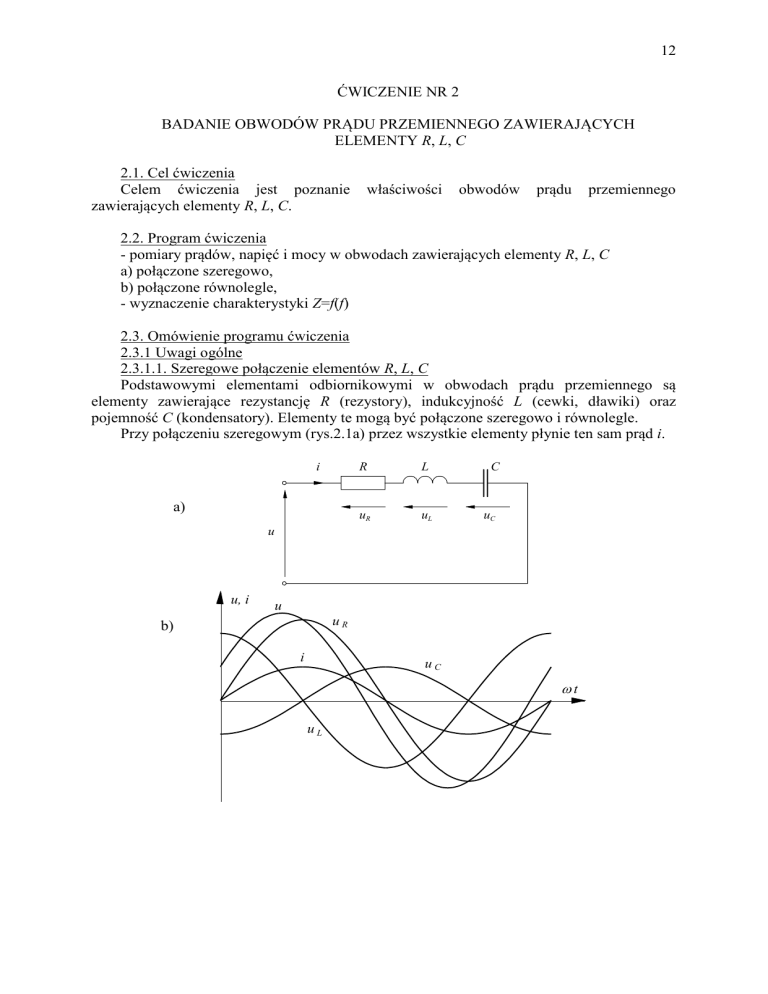
Przy połączeniu szeregowym (rys.2.1a) przez wszystkie elementy płynie ten sam prąd i.
i
a)
R
L
uR
uL
C
uC
u
u, i
u
uR
b)
i
uC
t
uL
13
d)
c)
UL
UL
XL
UC
XC
U
Z

UR

I
UC
R
Rys. 2.1 Obwód z elementami R, L, C połączonymi szeregowo; a) układ połączeń, b) przebiegi
czasowe prądu i napięć, c) wykres wektorowy, d) trójkąt impedancji.
W przypadku, gdy jest to prąd sinusoidalny, i  2 I sin  t , napięcia na elementach R, L, C
będą również sinusoidalne (rys.2.1b), a ich wartości chwilowe wyniosą:
u R  R i  2 IR sin  t
(1)
di


u L  L  2 I  L sin   t  
(2)
dt
2

1
1


(3)
uC   idt  2 I
sin  t  
C
C 
2
Z powyższych zależności wynika:
- napięcie na rezystancji uR jest w fazie z prądem,
- napięcie na indukcyjności uL wyprzedza prąd o kąt  /2,
- napięcie na pojemności uC jest opóźnione względem prądu o kąt  /2.
Wartości skuteczne tych napięć wynoszą:
(4)
U R  IR ,
(5)
U L  I L  I X L ,
UC  I
1
 I XC ,
C
(6)
gdzie: XL, XC - reaktancje: indukcyjna i pojemnościowa. Zgodnie z drugim prawem
Kirchhoffa, suma napięć chwilowych na poszczególnych elementach obwodu równa jest
napięciu wypadkowemu
(7)
u  u R  u L  uC
Ponieważ wszystkie napięcia składowe są funkcjami sinusoidalnymi o tej samej
częstotliwości, napięcie wypadkowe jest również sinusoidalne
(8)
u  2 U sin  t   
Wartość skuteczną napięcia wypadkowego (U) uzyskuje się w wyniku geometrycznego
zsumowania napięć skutecznych (4), (5) i (6)
U  U R U L U C
(9)
Równaniu (9) odpowiada wykres wektorowy przedstawiony na rys.2.1c, z którego
wynika:
U  U R2  U L  U C 
2
Kąt przesunięcia fazowego  między prądem i napięciem jest równy:
(10)
14
U L UC
(11)
UR
Stosunek skutecznych wartości napięcia i prądu na zaciskach danego obwodu nosi nazwę
impedancji
U
Z .
(12)
I
Zależność (12) często nazywana jest prawem Ohma dla obwodów prądu przemiennego.
Z rys. 2.1d, zwanego trójkątem impedancji, wynika
  arc tg
Z  R 2  X L  X C 
2
(13)
oraz
XL  XC
.
(14)
R
Z zależności (2) i (3) wynika z kolei, że napięcia UL i UC przesunięte są względem siebie
o 180. Oznacza to, że napięcia te w większym lub mniejszym stopniu kompensują się. Stan,
w którym dochodzi do pełnej kompensacji obu napięć (ULUC=0) nazywany jest rezonansem
napięć. Ponieważ UL=XLI, a UC=XCI rezonans napięć wystąpi, gdy
(15)
XL  XC
Częstotliwość fo , przy której dochodzi do rezonansu, nazywana jest częstotliwością
rezonansową. Jej wartość wynika z warunku (15) i wynosi:
1
(16)
fo 
2 LC
Podczas rezonansu napięć impedancja obwodu Z=R , zatem prąd w obwodzie osiąga
wartość maksymalną. W konsekwencji tego napięcia na cewce i kondensatorze mogą być
dużo większe od napięcia zasilającego układ. Zależność prądu oraz impedancji obwodu
szeregowego od częstotliwości pokazano na rys. 2.2.
  arc tg
Z, I
Z
R
I
f0
f
Rys. 2.2 Zależność impedancji oraz prądu od częstotliwości
Obwody rezonansowe znajdują zastosowanie jako filtry w układach elektronicznych.
2.3.1.2 Równoległe połączenie elementów R, L, C
Rys.2.3 przedstawia obwód z równolegle połączonymi elementami R, L, C.
15
IC
i
iR
u
iL
R
L
IR
iC
U

G

C
I
Y
IC
IL
IL
a)
b)
BL
BC
c)
Rys. 2.3. Obwód z elementami R, L, C połączonymi równolegle;
a) układ połączeń, b) wykres wektorowy c) trójkąt admitancji.
W obwodzie tym, zgodnie z I prawem Kirchhoffa, chwilowa wartość prądu wypadkowego i
jest równa sumie prądów chwilowych w poszczególnych gałęziach:
(17)
i  i R  i L  iC
Ponieważ wszystkie elementy tego obwodu są zasilane napięciem sinusoidalnym
u  2 U sin  t , prądy iR, iL oraz iC mają charakter sinusoidalny.
Prąd wypadkowy ma postać:
i  2 I sin t   
(18)
Jego wartość skuteczną (I) otrzymuje się w wyniku geometrycznego zsumowania prądów
skutecznych w poszczególnych gałęziach:
(19)
I  IR  IL  IC
Równaniu (19) odpowiada wykres wektorowy przedstawiony na rys. 2.3b, z którego
wynika:
I  I R2  I L  I C 
2
(20)
Kąt przesunięcia fazowego  pomiędzy prądem wypadkowym I i napięciem U wynosi:
I I
(21)
  arc tg L C
IR
Rozwiązanie obwodów równoległych upraszcza się po wprowadzeniu admitancji,
zdefiniowanej jako
1
I
Y 
(22)
Z U
Z rys. 2.3c, zwanego trójkątem admitancji, wynika że admitancja obwodu wynosi
Y  G 2  BL  BC 
2
gdzie:
1 I
G   R - konduktancja,
R U
I
1
BL 
 L - susceptancja indukcyjna,
XL U
I
1
BC 
 C - susceptancja pojemnościowa.
XC U
Kąt przesunięcia fazowego między prądem wypadkowym a napięciem jest równy:
(23)
16
BL  BC
(24)
G
Stan, w którym w obwodzie równoległym (rys.2.3a) dochodzi do pełnej kompensacji
prądów płynących w gałęziach zawierających elementy L i C (ILIC=0), nazywany jest
rezonansem prądów. Rezonans prądów wystąpi gdy:
BL  BC
Ma wtedy miejsce oscylacja prądu i energii między elementami L i C. Energia pola
1


magnetycznego cewki WL  L i 2  w każdej połówce okresu zamienia się na energię pola
2


1


elektrycznego kondensatora WC  C u 2  i odwrotnie. Prąd oscylujący nie jest pobierany ze
2


źródła mimo często dużych wartości prądów jakie płyną przez elementy L i C. Zjawisko to
wykorzystuje się w praktyce do budowy filtrów oraz do kompensacji mocy biernej.
W obwodach prądu przemiennego zawierających elementy R, L, C oprócz mocy czynnej,
która określa rzeczywistą przemianę energii P=I2 R , definiuje się dodatkowo moc bierną
Q=I2X i pozorną S=I2 Z=U I. Z rys. 2.4, zwanego trójkątem mocy, wynika:
P  S  cos   U  I cos 
(25)
Q  S sin   UI sin 
(26)
  arc tg
S  P2  Q2
(27)
Stosunek P/S=cos nosi nazwę współczynnika mocy.
S
Q
=
(
Q
-Q
)
L
C

P
Rys. 2.4 Trójkąt mocy
2.3.2 Badanie obwodu szeregowego
Pomiary napięć, prądu i mocy pobranej z sieci przez elementy R, L, C połączone
szeregowo prowadzone będą w układzie jak na rys. 2.5.
17
Do oscyloskopu
I
A
Rb
*
* W
R1
R
L
W1
UR1
V
f
UR
UL
URL
V
V
UC
V
C1
C2
C3
U
AT
W
Rys. 2.5 Układ pomiarowy obwodu szeregowego
W układzie tym cewkę rzeczywistą przedstawiono w postaci dwóch elementów
idealnych: rezystora R i cewki o indukcyjności L.
Przed włączeniem układu należy ustawić autotransformator w pozycji U=0. Po
zamknięciu wyłącznika W należy zwiększać napięcie zasilające zwracając uwagę na to, by
nie przekroczyło ono wartości napięć znamionowych podanych na elementach L i C. Pomiary
należy wykonać dla trzech różnych wartości pojemności. Wyniki pomiarów zestawić w tabeli
2.1.
Tabela 2.1.
L
p
Moc
U
I
V
A

dz
cW
W/dz
cos UR1 URL
P
W
-
V
V
UR
UL
UC
R1
R
XL
L
XC
C
Z Uwagi
V
V
V



mH

F 
f =...Hz
W powyższej tabeli:
P    cW ,
P
cos  
,
UI
U R  U cos   U R1 ,
2
U L  U RL
 U R2 ,
U R1
,
I
U
R R ,
I
R1 
18
UL
,
I
X
L L ,
2f
1
.
XC 
2fC
Po wyłączeniu napięcia zasilającego nie należy dokonywać żadnych zmian w układzie
połączeń, dopóki napięcie na kondensatorze nie zmaleje do bezpiecznej wartości, co można
stwierdzić obserwując wskazania woltomierza włączonego na jego zaciski.
Na podstawie wyników pomiarów i obliczeń należy narysować wykres wektorowy prądu
i napięć przy wybranej pojemności (rys.2.6). Przy tej pojemności należy obliczyć
częstotliwość rezonansową, a następnie określić wartość Z przy f = 0,25; 0,5; 0,75; 1,0 i
1,25fo. Wyniki obliczeń zestawić w tabeli 2.2. Na ich podstawie wykreślić zależność Z=f(f)
(rys.2.2).
XL 
UR
U R1
UL
UC
U RL
U

U R1
I
Rys. 2.6 Wykres wektorowy napięć obwodu szeregowego z cewką rzeczywistą
Lp.
f
Hz
Tabela 2.2
Z

2.3.3 Badanie obwodu równoległego
Pomiary prądu i mocy pobranej z sieci przez elementy R, L, C połączone równolegle
prowadzone będą w układzie jak na rys. 2.7.
19
I
A
*
* W
W
I R1
I RL
IC
W1
W2
W3
R
V
C
R1
AT
L
Rys. 2.7. Układ pomiarowy obwodu równoległego
W układzie tym rzeczywistą cewkę przedstawiono w postaci dwóch elementów
idealnych: rezystora R i cewki o indukcyjności L. Przed uruchomieniem układu
autotransformator należy ustawić w położeniu U=0. Po zamknięciu wyłącznika W należy
zwiększyć napięcie zasilające do wartości znamionowej podanej na elementach R, L i C.
Następnie zamykając lub otwierając wyłączniki W1, W2 i W3 należy wybrać kolejną
kombinację połączeń elementów tworzących obwód. Dla każdej kombinacji przy U=Un
odczytać wartość prądu i mocy. Wyniki pomiarów zestawić w tabeli 2.3. Na ich podstawie
wykonać wykres wektorowy prądów dla przypadku równoległego połączenia wszystkich
elementów (rys.2.8).
IC
I R1
U

I
IC
I RL
I R1
Rys. 2.8 Wykres wektorowy prądów obwodu równoległego z rzeczywistą cewką
Tabela 2.3
sposób połączenia
U
V
R1
(RL)
C
R1(RL)
R1 C
C (RL)
R1 (RL) C
I
A

dz
Moc
cW
W/dz
P
W
cos
-
20
2.4. Opracowanie wyników
Sprawozdanie z ćwiczenia powinno zawierać:
- opracowany protokół z wynikami pomiarów i obliczeń,
- wykresy wektorowe napięć i prądów,
- wykres Z=f(f) dla obwodu szeregowego,
- uwagi i wnioski.
2.5. Pytania kontrolne
1. W jakich układach i kiedy zachodzi rezonans napięć?
2. W jakich układach i kiedy zachodzi rezonans prądów?
3. Jaki warunek musi być spełniony, aby w obwodzie R, L, C wystąpił rezonans?
4. Podaj zależność na częstotliwość rezonansową.
5. Dlaczego przy rezonansie napięć napięcia na cewce i kondensatorze mogą być większe
od napięcia zasilającego?