Indukcja elektromagnetyczna

Indukcja elektromagnetyczna
Gdy w polu magnetycznym porusza się przewodnik stanowiący zamknięty obwód, to – jak
pokazuje doświadczenie – w obwodzie tym może powstać prąd elektryczny (prąd
indukcyjny). Przepływ prądu jest skutkiem występowania w takim obwodzie siły
elektromotorycznej indukcji. Siła elektromotoryczna jest rozłożona w sposób ciągły; można
zatem postrzegać ją jako sumę sił elektromotorycznych indukowanych w poszczególnych
krótkich odcinkach tego obwodu. Przed obliczeniem siły elektromotorycznej w całym
obwodzie zamkniętym rozpatrzmy zjawiska jakie zachodzą w odcinku przewodnika
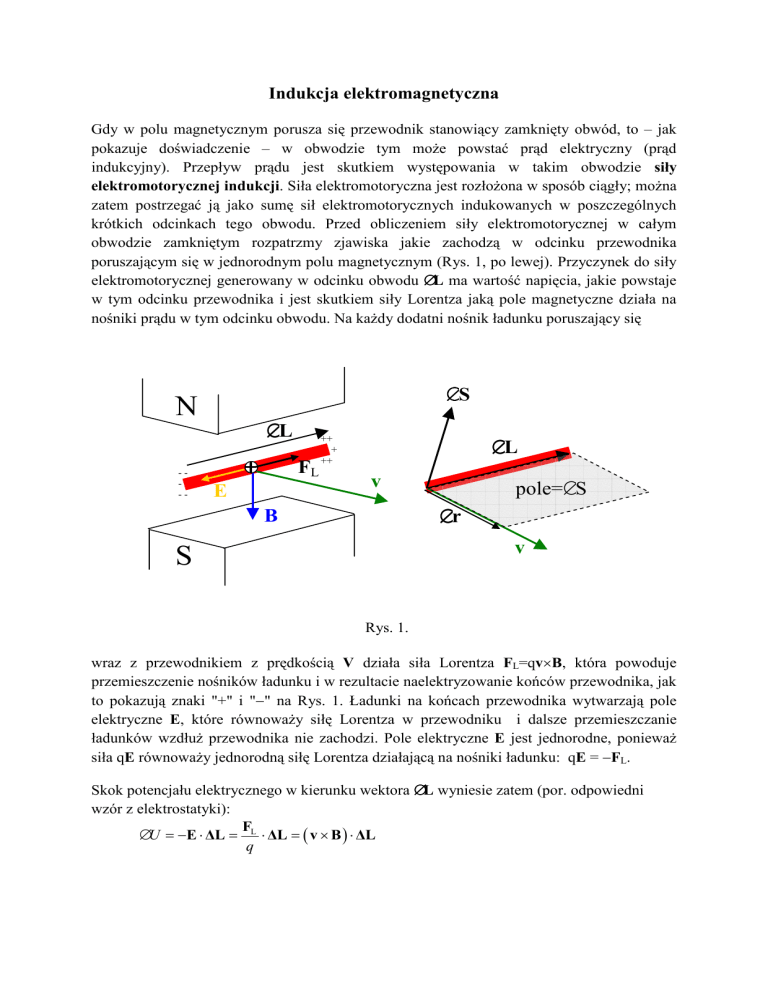
poruszającym się w jednorodnym polu magnetycznym (Rys. 1, po lewej). Przyczynek do siły
elektromotorycznej generowany w odcinku obwodu ∆L ma wartość napięcia, jakie powstaje
w tym odcinku przewodnika i jest skutkiem siły Lorentza jaką pole magnetyczne działa na
nośniki prądu w tym odcinku obwodu. Na każdy dodatni nośnik ładunku poruszający się
∆S
N
---
∆L
FL
E
∆L
++
+
++
v
pole=∆S
∆r
B
v
S
Rys. 1.
wraz z przewodnikiem z prędkością V działa siła Lorentza FL=qv×B, która powoduje
przemieszczenie nośników ładunku i w rezultacie naelektryzowanie końców przewodnika, jak
to pokazują znaki "+" i "−" na Rys. 1. Ładunki na końcach przewodnika wytwarzają pole
elektryczne E, które równoważy siłę Lorentza w przewodniku i dalsze przemieszczanie
ładunków wzdłuż przewodnika nie zachodzi. Pole elektryczne E jest jednorodne, ponieważ
siła qE równoważy jednorodną siłę Lorentza działającą na nośniki ładunku: qE = −FL.
Skok potencjału elektrycznego w kierunku wektora ∆L wyniesie zatem (por. odpowiedni
wzór z elektrostatyki):
F
∆U = −E ⋅ ∆L = L ⋅ ∆L = ( v × B ) ⋅ ∆L
q
Gdybyśmy spięli końce tego odcinka przewodnikiem, to napięcie ∆U spowodowałoby
przepływ w nim prądu elektrycznego. Napięcie ∆U stanowi zatem siłę elektromotoryczną
(∆E)∆L generowaną w odcinku przewodnika ∆L. Wynosi ona:
(∆ε ) ∆L = ( v × B ) ⋅ ∆L = ∆L ⋅ ( v × B ) = ( ∆L × v ) ⋅ B
W powyższym przekształceniu najpierw skorzystaliśmy z przemienności iloczynu skalarnego,
a następnie z tożsamości wektorowej: a ⋅ ( b × c ) = ( a × b ) ⋅ c . Zauważmy jeszcze, że wyrażenie
(∆
∆L×v) można przekształcić:
∆L × v = ∆L ×
∆r 1
1
1
= ( ∆L × ∆r ) = − ( ∆r × ∆L ) = − ∆S
∆t ∆t
∆t
∆t
a zatem:
( ∆Φ )∆L
1
∆S ⋅ B = −
∆t
∆t
∆S·B jest strumieniem indukcji magnetycznej B przez powierzchnię ∆S, zaś ∆S jest
(∆Φ)∆L=∆
tu wektorem powierzchni skierowanej zakreślonej w czasie ∆t przez odcinek ∆L przewodnika
(lub przez wektor ∆L) (bo wartość iloczynu wektorowego jest polem równoległoboku
zbudowanego na mnożonych wektorach).
(∆ε ) ∆L = −
Gdy w polu magnetycznym porusza się zamknięty obwód, to siłę elektromotoryczną
powstającą na całej długości obwodu można uzyskać sumując przyczynki pochodzące od
krótkich jego odcinków; w każdym z tych odcinków zachodzą te same zjawiska co opisane
powyżej. Ilustruje to Rys. 2. Sumując przyczynki do siły elektromotorycznej pochodzące
∆S ∆L
∆r
B
Rys. 2
od poszczególnych fragmentów obwodu oznaczonych strzałkami na Rys. 2 otrzymamy:
ε = ∑  − ∆Φi  = − ∆Φ
i

∆t 
∆t
∆Φ oznacza tu sumaryczną zmianę strumienia indukcji B przenikającego przez obwód.
Z powyższego wzoru w granicy z ∆t→0 wynika prawo indukcji elektromagnetycznej
− prawo Faradaya:
ε = − dΦ
dt
Znak „minus” w prawie indukcji uwzględnia relacje między kierunkiem sumowania sił
elektromotorycznych na poszczególnych odcinkach obwodu, zwrotem wektora powierzchni
skierowanej dla tego obwodu i zwrotem wektora indukcji magnetycznej B.
Zauważmy, że w powyższych rozważaniach nie występuje natężenie prądu indukcyjnego, co
oznacza, że prąd nie musi się pojawić w tym zjawisku i obecność przewodnika nie jest
konieczna. W istocie zjawisko indukcji polega na powstawaniu wirowego pola
elektrycznego, tj. pola elektrycznego o zamkniętych liniach sił. Pole to może spowodować
przepływ prądu indukcyjnego jeżeli krzywa C jest przewodnikiem, ale pole elektryczne
istnieje niezależnie od tego, czy prąd indukcyjny występuje, czy też nie występuje. Tak więc
zjawisko indukcji elektromagnetycznej polega przede wszystkim na wytwarzaniu w
przestrzeni wirowego pola elektrycznego przez zmienne pole magnetyczne. Prądy
indukcyjne są tylko następstwem tego pola i pojawiają się, gdy w tym indukowanym polu
elektrycznym znajduje się przewodnik.