1 Zbadano grupę krwi 100 osób i otrzymano następujące wyniki

Zadanie 3.
1
Zbadano grupę krwi 100 osób i otrzymano następujące wyniki: grupę O miało 39 osób, A - 44,
B - 11, AB - 6 osób.
a) Czy na podstawie tych danych można przyjąć hipotezę o równomiernym rozkładzie wszystkich
grup krwi w badanej populacji?
b) Zweryfikować hipotezę, że prawdopodobieństwa występowania grup krwi O, A, B, AB sa w
stosunku 4 : 4 : 1 : 1 . Przyjęć poziom istotności a = 0.05.
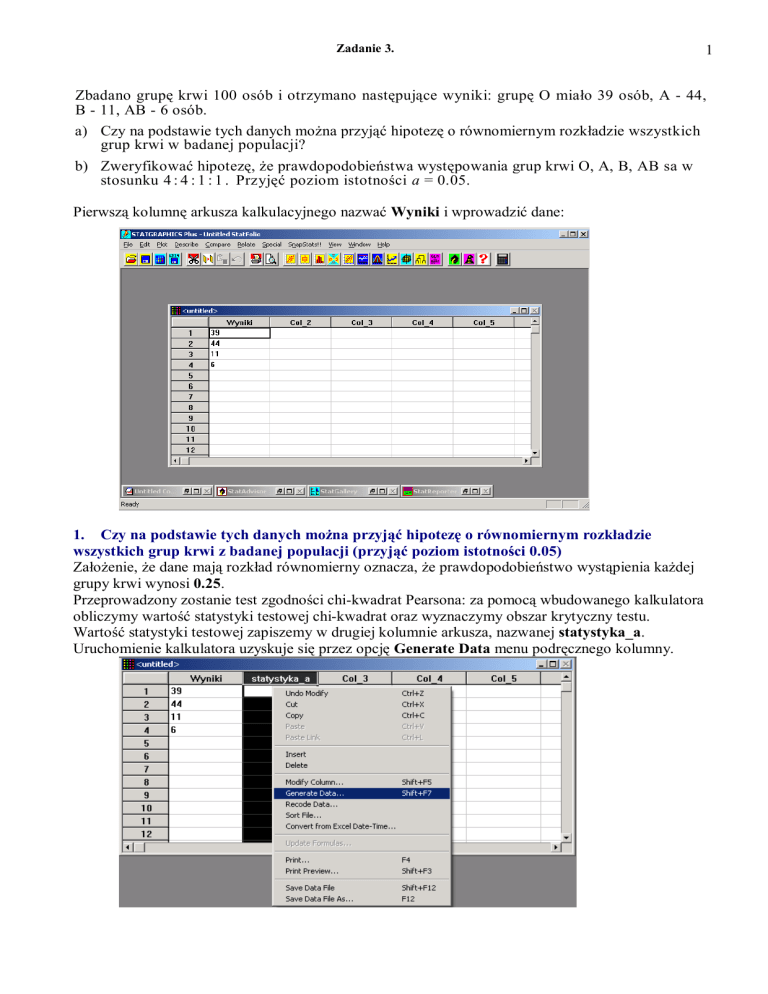
Pierwszą kolumnę arkusza kalkulacyjnego nazwać Wyniki i wprowadzić dane:
1. Czy na podstawie tych danych można przyjąć hipotezę o równomiernym rozkładzie
wszystkich grup krwi z badanej populacji (przyjąć poziom istotności 0.05)
Założenie, że dane mają rozkład równomierny oznacza, że prawdopodobieństwo wystąpienia każdej
grupy krwi wynosi 0.25.
Przeprowadzony zostanie test zgodności chi-kwadrat Pearsona: za pomocą wbudowanego kalkulatora
obliczymy wartość statystyki testowej chi-kwadrat oraz wyznaczymy obszar krytyczny testu.
Wartość statystyki testowej zapiszemy w drugiej kolumnie arkusza, nazwanej statystyka_a.
Uruchomienie kalkulatora uzyskuje się przez opcję Generate Data menu podręcznego kolumny.
Zadanie 3.
Wprowadzenie operatora sumy
Wpisanie formuły wyznaczającej wartość statystyki chi-kwadrat Pearsona w przypadku rozkładu
równomiernego:
Wartość statystyki wynosi 44.56.
W następnej kolumnie zapisana zostanie wartość kwantyla rzędu 0.95 (dla =0.05) rozkładu
chi-kwadrat o 3 stopniach swobody.
2
Zadanie 3.
Wyznaczenie kwantyla
rozkładu chi-kwadrat
Stąd obszar krytyczny testu na przyjętym poziomie istotności =0.05 ma postać:
W = [7.775, + ∞)
Wynik:
3
Zadanie 3.
2.
Zweryfikować hipotezę, że prawdopodobieństwo występowania grup krwi
0, A, B i AB są w stosunku 4 : 4 : 1 : 1
Założenie, że grupy krwi występują w określonym stosunku oznacza, że prawdopodobieństwo
wystąpienia grup 0, A, B i AB wynosi odpowiednio
0.4 0.4 0.1 0.1
Dane te wpisujemy
do kolejnej kolumny arkusza,
natomiast w następnej
kolumnie obliczymy wartość
statystyki
chi-kwadrat
dla powyższych danych
Obliczanie wartości statystyki
Wartość statystyki:
Wynik:
4