Politechnika Śląska w Gliwicach
Wydział Automatyki Elektroniki i Informatyki
Instytut Elektroniki
Zbigniew Krajewski
Klasyfikacja Strukturalna Białek
Za Pomocą
Maszyn Wektorów Podpierających
AUTOREFERAT ROZPRAWY DOKTORSKIEJ
Promotor:
Prof. dr hab. inż. Ewaryst Tkacz
Gliwice 2011
1. Wstęp ..................................................................................................................................... 3
2 Wprowadzenie do bydowy strukturalnej białek ................................................................ 4
2.2 Struktura i właściwości aminokwasów......................................................................... 4
2.2.1 Właściwości aminokwasów..................................................................................... 5
2 Struktura białka ..............................................................Błąd! Nie zdefiniowano zakładki.
2.1 Wiązanie peptydowe. ..................................................................................................... 7
2.2 Kąty dwuścienne łańcucha białkowego ........................................................................ 7
2.3 Podział złożoności struktury białka.............................................................................. 7
2.4 Regularne struktury drugorzędowe ............................................................................. 8
2.4.1 Struktury helikalne. ................................................................................................ 8
2.4.2 Arkusz β ................................................................................................................... 8
2.5 Klasy strukturalne.......................................................................................................... 9
3 Metoda SVM .......................................................................................................................... 9
3.1 Metoda SVM dla danych liniowo separowalnych ....................................................... 9
3.2 Metoda SVM dla danych liniowo nieseparowalnych ................................................ 10
3.3 Wykorzystanie funkcji jądra....................................................................................... 10
3.4 Zalety metody SVM : ................................................................................................... 11
3.5 Wady metody SVM:..................................................................................................... 11
4 Cele i tezy pracy................................................................................................................... 12
4.1 Cele pracy...................................................................................................................... 12
4.2 Tezy pracy ..................................................................................................................... 12
4.3 Dobór danych................................................................................................................ 12
4.4 Ekstrakcja cech ............................................................................................................ 13
4.5 Selekcja cech ................................................................................................................. 13
5 Wybrane wyniki badań....................................................................................................... 15
5.1 Porównanie predykcji klas strukturalnych uzyskanych metodami minimalnoodległościowymi oraz metodą SVM z użyciem cech komponentów aminokwasów
(AAC)................................................................................................................................... 15
5.2 Predykcja klas strukturalnych domen białkowych przy pomocy SVM dla
rozszerzonych cech komponentów aminokwasów .......................................................... 16
5.2.1 Cecha reprezentująca długość łańcucha domeny białkowej ............................. 16
5.2.2 Wpływ cech reprezentujących efekt kolejności aminokwasów łańcucha
domeny białkowej........................................................................................................... 16
5.4 Selekcja cech istotnych............................................................................................. 17
6 Wnioski końcowe pracy ..................................................Błąd! Nie zdefiniowano zakładki.
7 Literatura .........................................................................Błąd! Nie zdefiniowano zakładki.
2
1. Wstęp
W nauce panuje przekonanie, że w szczególności DNA jak i RNA stanowią
zmagazynowaną pełną informację o wszystkich procesach życiowych zachodzących w
organizmach żywych. Zarówno ekspresja genów jak i jej regulacja ściśle zależą od sekwencji
nukleotydów tworzących długą cząsteczkę polimeru występującego w komórkach
organizmów żywych, w strukturze podwójnej, prawoskrętnej helisy DNA. W przeważającej
części, aktywny DNA zorganizowany jest w krótkie fragmenty kodu zwane genami. W
najbardziej rozpowszechnionym ujęciu, genem będziemy nazywać fragment DNA, który jest
odpowiedzialny za kodowanie jednego łańcucha polipeptydu białkowego. Choć bardziej
precyzyjna definicja genu określa go jako fragment DNA umożliwiający komórce
wytworzenie dowolnego typu RNA (np. rRNA, tRNA,mRNA) to jednak w przeważającej
mierze celem aktywności genów jest wytworzenie łańcucha polipeptydu funkcjonalnego
białka. Można powiedzieć, że DNA stanowi zestaw instrukcji określających przede
wszystkim sekwencję aminokwasów łańcucha białkowego, choć również :
a) intensywność i czas jego wytwarzania,
b) warunki, w jakich białko powinno być wytwarzane,
c) przedział komórki, do jakiej białko będzie przesłane
d) oraz informację w których tkankach i w jakiego typu komórkach białko ma
powstawać.
Zatem istnieje bezpośrednie powiązanie pomiędzy informacją zakodowana w DNA i
sekwencją, a więc budową tworzonego łańcucha polipeptydu. Obserwujemy trzystopniowy
system realizacji procesów życiowych związanych z rozwojem i funkcjonowaniem
organizmów żywych. Stabilna struktura DNA zarządza procesami życiowymi za
pośrednictwem fragmentów RNA, dedykowanych do wytworzenia odpowiednich rodzajów
białek i to zwykle białka a nie DNA czy nawet RNA, posiadają właściwą funkcję
wykonawczą.
Odnosząc się do różnorakich funkcji białek należałoby, wspomnieć ich znane podstawowe
funkcje [FunBia]:
a) Funkcja transportu małych cząsteczek i jonów np.
hemoglobina odpowiedzialna za przenoszenie tlenu krwinek czerwonych
mioglobina odpowiedzialna za przenoszenie tlenu w mięśniach
transferyna odpowiedzialna za transport atomów żelaza w osoczu krwi do tkanek
b) Magazynowanie np.
ferrytyna odpowiedzialna za przechowywanie jonów żelaza w wątrobie
c) Wytwarzanie i przekazywanie impulsów nerwowych.
Reakcja komórek nerwowych na określone bodźce odbywa się z udziałem białek
receptorowych np.
rodopsyna – światłoczuły barwnik występujący w komórkach pręcikowych siatkówki
oka
d) Katalizy enzymatycznej np.
anhydraza węglanowa odpowiedzialna za katalizę uwodnienia dwutlenku węgla
(CO2 + H2O → H2CO3 → H+ + HCO3 ), występuje m. in. w erytrocytach gdzie m. in. pomaga
w wydalaniu tlenku węgla.
e) Regulacja przenikalności błony komórkowej
Rolą tych białek jest regulacja stężenia metabolitów wewnątrz komórki
f) Funkcje ruchu uporządkowanego np.
aktyna i miozyna wchodzące w skład mięśni.
3
g) Kontrola wzrostu i róznicowania
Kontrola ekspresji genów i jej kolejności, które są podstawowymi warunkami wzrostu
i różnicowania komórek.
h) Funkcje immunologiczne.
Białka używane przez system immunologiczny do identyfikacji i neutralizacji obcych
ciał takich jak bakterie czy wirusy.
i) Przyleganie komórek np.
kadhedryny – ułatwiają przyleganie komórek tego samego rodzaju
j) Budulcowe np.:
kolagen – białko fibrylarne posiadające dużą odporność na rozciąganie nadające
elastyczność m. in. tkance kostnej i mięśniowej.
elastyna – białko fibrylarne występujące m. in. w ścięgnach, więzadłach, tkance
płucnej oraz większych naczyniach krwionośnych. Po rozciągnięciu lub ściśnięciu
charakteryzuje się właściwością odzyskiwania pierwotnego kształtu.
k) Regulatorowe.
Białka wykorzystywane do regulacji przebiegu procesów biochemicznych np. w
hormonach takich jak insulina czy hormon wzrostu.
Funkcje białek ściśle związane są z charakterystyczną dla danego białka strukturą
trójwymiarową przybierającą, w przypadku różnych białek, często bardzo złożone i
nieregularne formy. Z kolei ta swoista trójwymiarowa budowa białka jest ściśle uzależniona
od sekwencji reszt aminokwasów wchodzących w jego skład. W związku z tym, przedmiotem
analiz w wielu opracowaniach stała się predykcja i klasyfikacja trójwymiarowej struktury
białka na podstawie jego sekwencji reszt aminokwasów.
2 Wprowadzenie do budowy strukturalnej białek
2.2 Struktura i właściwości aminokwasów
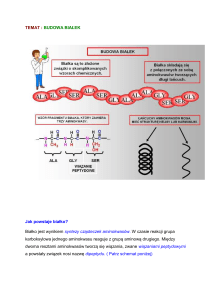
Białko składa się z podjednostek, aminokwasów połączonych przy pomocy wiązania
peptydowego. Aminokwasy białkowe natomiast to związki chemiczne, w których możemy
wyszczególnić następujące składowe: atom węgla α (Cα), grupę aminową, grupę
karboksylową i łańcuch boczny R (rys 1.1.1 a).
CO2H
H
H
N
H2N
C
CO2H
CH
H2C
CH2
CH2
R
(a)
(b)
Rysunek 1.1.1 Wzory: ogólny α aminokwasów (a) oraz proliny (b)
Pewien wyjątek stanowi prolina, która posiada drugorzędową grupę aminową, będącą częścią
pierścienia (rys 1.1.1 b) [Shawn 2002; Hart 1999]. W białkach występujących w środowisku
naturalnym znajdowanych jest ok. 140 różnych reszt aminokwasowych [Szymański 2007].
4
Tylko 20 z nich kodowanych jest w DNA. Wyszczególnia się dodatkowe dwa rzadziej
występujące aminokwasy kodowane w określonych warunkach za pomocą kodonów „stop”
wstawiane do białek podczas procesu translacji mRNA (UGA –selenocysteina, UAG –
pyrolizyna – rys.1.1.2) [Szymański 2007, Buxbaum 2007]. Inne rzadziej występujące
aminokwasy powstają na skutek modyfikacji typowych aminokwasów już wbudowanych w
strukturę białka np. hydroksylizyna czy hydroksyprolina [Solomon 2007].
W środowisku wodnym aminokwasy przyjmują postać jonów amfoterycznych tzw. struktury
zwitterion [Hames 2002]. Grupa karboksylowa ulega dysocjacji uzyskując ładunek ujemny,
natomiast do grupy aminowej, która uzyskuje ładunek dodatni, dołączany jest wodór [Voet
2004] (rys.1.1.3).
Rysunek 1.1.3 Uogólniony model atomowy i wzór struktury zwitterion.
2.2.1 Właściwości aminokwasów
Do najczęściej wyszczególnianych właściwości aminokwasów należą [Dasgupta AAI,
Dasgupta AAII, Dasgupta PSI]:
1) Rozmiar i kształt
Najczęściej dokonuje się podziału na małe (w tym bardzo małe) i pozostałe.
Poszczególne reszty kwasowe określa się indywidualnie w zależności od długości
łańcucha czy grubości cząsteczki.
Do kategorii małych zalicza się cysteinę, treoninę, kwas asparaginowy, asparaginę,
prolinę .W tym do bardzo małych zalicza się : glicynę, alaninę, serynę, cysteinę. Małe
reszty aminokwasów pozwalają na większą elastyczność struktury białkowej,
szczególnie przy przechodzeniu z jednej struktury drugorzędowej w drugą.
2) Ładunek
Niektóre reszty aminokwasów obdarzone są ładunkiem. Reagują z innymi
cząsteczkami spolaryzowanymi lub jonami obdarzonymi ładunkiem przeciwnym.
Do grupy aminokwasów zasadowych, naładowanych dodatnio zaliczamy: lizynę,
argininę, histydynę.
Do grupy aminokwasów kwasowych naładowanych ujemnie zaliczamy: kwas
asparaginowy, kwas glutaminowy.
5
3) Polarność
Cząsteczki nie obdarzone ładunkiem i spolaryzowane posiadają w swoich łańcuchach
bocznych tlen lub azot, często wiążą się z innymi cząsteczkami spolaryzowanymi np.
cząsteczkami wody tworząc wiązania wodorowe.
Do grupy aminokwasów polarnych możemy zaliczyć: tryptofan, tyrozynę, treoninę,
cysteinę, serynę, asparaginę, glutaminę, histydynę, argininę, lizynę, kwas
glutaminowy, kwas asparaginowy.
4) Hydrofobowość
Reszty o długich łańcuchach węglowo-wodorowe lub tworzące grube węglowowodorowe cząsteczki stowarzyszają się ze sobą ze względu na oddziaływanie sił
wiązań wodorowych pomiędzy cząsteczkami wody. Tworzące sieć wiązań
wodorowych cząsteczki wody oraz spolaryzowane cząsteczki aminokwasów powodują
wypychanie cząsteczek niespolaryzowanych z sieci cząsteczek spolaryzowanych
skupiając je w jednym miejscu tworząc tzw. wiązania hydrofobowe [Trojanowski
1977]. W środowisku wodnym reszty hydrofobowe zajmują wewnętrzne struktury
białka, na zewnątrz znajdują się cząsteczki hydrofilowe tzn. biorące udział w
oddziaływaniu z siecią spolaryzowanych cząsteczek wody oraz innych części łańcucha
białkowego. W środowisku gdzie otoczenie stanowią cząsteczki hydrofobowe jak
lipydy w przypadku błony komórkowej reszty hydrofobowe znajdują się na zewnątrz
struktury białkowej a reszty spolaryzowane znajdują się w jej środku. Spowodowane
jest to oddziaływaniami między resztami spolaryzowanymi grupującymi je razem we
wnętrzu struktury białka.
Do grupy aminokwasów hydrofobowych zalicza się:
glicynę, alaninę, cysteinę, treoninę, valinę, leucynę, izoleucynę, metioninę,
fenyloalaninę, tryptofan, tyrozynę, histydynę, lizynę.
5) Aromatyczność
Są to reszty zawierające w swojej strukturze pierścień aromatyczny. Zazwyczaj
stanowią silnie hydrofobowe grube cząsteczki.
W grupie aminokwasów aromatycznych znajdują się:
fenyloalanina, tyrozyna, tryptofan oraz histydyna.
6) Alifatyczność
Reszty alifatyczne stanowią zwykle dłuższe czy krótsze łańcuchy węglowo-wodorowe
wykazujące cechy silnie hydrofobowe.
Do grupy aminokwasów alifatycznych zaliczamy:
leucynę, izoleucynę oraz walinę. Ich grupy boczne stanowią otwarte łańcuchy
węglowe, są hydrofobowe i niepolarne.
6
2.1 Wiązanie peptydowe.
Białka stanowią liniowe sekwencje aminokwasów połączone przy pomocy wiązań
peptydowych [Hames 2002]. Są to wiązania kowalencyjne pomiędzy grupą aminową jednego
aminokwasu i grupą karboksylową drugiego (rys. 1.2.1.1)
H
H
H
+
H3N
C
+
C
+
H3N
C
-
O
R1
H
O
O
C
O
=
+
O
R2
H3N
C
C
R1
O
N
C
H
R2
C
+
H2O
O-
Rysunek 1.2.1.1 Tworzenie wiązania peptydowego
Wiązania peptydowe są sztywne a grupy peptydowe posiadają charakter planarny, atomy
O=C-N-H leżą w jednej płaszczyźnie (rys. 1.2.1.2). Swobodna rotacja zachodzi dla połączeń
między grupami peptydowymi a węglem α, z którym połączona jest reszta aminokwasu (Cα-C
, Cα-N).
sztywne grupy peptydowe
H
H
O
Cα
R1
C
H
O
N
Cα
H
R2
C
H
O
N
Cα
H
R3
C
N
Cα
H
R4
swobodna rotacja
Rysunek 1.2.1.2 Łańcuch polipeptydu, połączonych reszt aminokwasów.
Typowa konformacja tego wiązania to konfiguracja trans, w której atomy węgla Cα kolejnych
reszt oraz atomy tlenu i azotu znajdują się po przeciwległych stronach wiązania peptydowego.
Konfiguracja cis zachodzi niezwykle rzadko z uwagi na wzajemne przestrzenne
oddziaływania reszt aminokwasów
2.2 Kąty dwuścienne łańcucha białkowego
Konformację łańcucha białkowego, którego składową stanowią charakterystyczne sztywne
grupy wiązania peptydowego, połączone do dwóch atomów węgla Cα kolejnych reszt
aminokwasów, można opisać przy pomocy dwóch kątów dwuściennych Φ oraz Ψ [Voet 2004,
Dasgupta PSI].
2.3 Podział złożoności struktury białka
Wzajemna relacja przestrzenna atomów białka rozpatrywana jest zwykle na czterech
poziomach złożoności strukturalnej [Voet 2004, Dasgupta PSI, Dasgupta PSII]. Wyróżniamy
strukturę pierwszo, drugo, trzecio i czwartorzędową. Struktura pierwszorzędowa określa
sekwencję kolejno po sobie następujących reszt aminokwasów w porządku od przyłącza N do
C. Struktura drugorzędowa to przestrzenny regularny układ łańcucha aminokwasów
zlokalizowanych w pobliżu, wzdłuż sekwencji liniowej. Trójwymiarową strukturę całego
7
łańcucha polipeptydu określa struktura trzeciorzędowa. W skład wielu białek wchodzi więcej
niż jeden łańcuch polipeptydu połączonych zwykle innymi wiązaniami niż kowalentne, bądź
znacznie rzadziej przy pomocy mostków dwusiarczkowych. Przestrzenne rozmieszczenie tych
jednostek określa czwartorzędowa struktura białka
2.4 Regularne struktury drugorzędowe
Na drugorzędową strukturę białka składają się w przeważającym stopniu regularne, i
powtarzające się motywy lokalnego rozmieszczenia aminokwasów takie jak helisy, wstęgi,
arkusze, zwroty czy pętle.
Helisy to skręcone dookoła węgla α, w określonym stałym stopniu, łańcuchy
polipeptydu Helisę charakteryzuje więc pewna stała wartość kąta Φ i Ψ. Alternatywną
wielkością, która może charakteryzować helisę jest ilość jednostek peptydu (reszt
aminokwasów) przypadających na jeden obrót oznaczony przez – n oraz skok gwintu – p
oznaczający długość jednego obrotu helisy wzdłuż jej osi pionowej .
2.4.1 Struktury helikalne.
Często występującym motywem struktury drugorzędowej jest struktura prawoskrętnej αhelisy. Jest to jedyna struktura helikalna znajdująca się w zakresie wartości kątów torsyjnych
Φ=-57° i Ψ=-47°. Wartość parametru n wynosi 3.6 reszt na obrót a skok p wynosi 5.4 Å.
Wiązania stabilizujące α-helisę to wiązania wodorowe pomiędzy wiązaniem N-H grupy
amidowej a wiązaniem C=O grupy karbonylowej n-4 reszty. Dodatkowo rdzeń α-helisy jest
ciasno upakowany zwiększając stabilizację przez działanie sił van der Waalsa. Reszty
skierowane są na zewnątrz nie powodując konfliktów przestrzennych między atomami [Voet
2004, Dasgupta PSII].
2.4.2 Arkusz β
Arkusz β posiada kąty dwuścienne w preferowanym obszarze diagramu Ramachandrana
[Voet 2004, Dasgupta PSII]. Podobnie jak w przypadku α-helisy stabilizację struktury
zapewniają wiązania wodorowe, jednak w przeciwieństwie do struktury α-helisy gdzie
istniały wiązania pomiędzy sąsiadującymi segmentami polipeptydu w obrębie jednego
łańcucha, tutaj występują raczej wiązania pomiędzy segmentami łańcuchów sąsiadujących.
Arkusz β posiada dwa warianty struktury: równoległą i antyrównoległą. Równoległy arkusz β
to struktura połączonych wiązaniami wodorowymi łańcuchów polipeptydu biegnących w tym
samym kierunku. Antyrównoległy arkusz β to połączenie łańcuchów polipeptydu biegnących
w przeciwnych kierunkach .
Arkusz β jest bardzo często występującym motywem w białkach. Zawiera od 2 do aż 22
włókien polipeptydu, średnia wartość to połączonych 6 łańcuchów. Łańcuch polipeptydu w
strukturze arkusza β zawiera do 15 reszt, średnio jego długość wynosi 6 reszt aminokwasów.
Równoległy arkusz β zawierająca w swojej strukturze mniej niż 5 włókien polipeptydu
występuje rzadko. Sugeruje to, że równoległy arkusz β jest mniej stabilny niż antyrównoległy,
prawdopodobnie z powodu tego, że połączenia wodorowe w równoległym arkuszu β są nieco
odkształcone w porównaniu z połączeniami w arkuszu antyrównoległym. Mieszane
równoległe i antyrównoległe arkusze występują często jednak średnio tylko z ok. 20%
udziałem arkusza równoległego.
8
2.5 Klasy strukturalne
Chociaż trójwymiarowa struktura białek jest niezwykle złożona i nieregularna, jednak ich
ogólny układ struktury jest zaskakująco prosty i regularny. Białka posiadają bardzo podobny
bądź identyczny wzorzec trójwymiarowej struktury pomimo tego, że mogą posiadać różne
sekwencje aminokwasów czy biochemiczne funkcje . Levit i Chothia wprowadzili koncepcję
strukturalnej klasy opartej na obserwacji topologii łańcucha polipeptydu w 31 białkach
globularnych. Wprowadzili cztery podstawowe klasy :α, β , α/β, α+β z przeważającym
udziałem struktur odpowiednio: helisy α, arkusza β, występujących naprzemiennie struktur
helisy α i arkusza β (w przeważającej mierze równoległe struktury β), rozdzielonych
obszarów struktur α i β (w przeważającej mierze antyrównoległe struktury arkusza β) [Levitt
1976].
3 Metoda SVM
Metoda SVM (Metoda maszyn wektorów podpierających) jest jedną z technik uczenia
maszynowego z nauczycielem wykorzystywana przede wszystkim jako metoda klasyfikacji i
regresji. Z uwagi na swoje zalety bywa coraz częściej używana w miejsce starszych metod
heurystycznych takich jak np. sieci neuronowe. Metoda SVM użyta jako klasyfikator pozwala
na rozpoznanie klas danych po uprzednim poddaniu klasyfikatora procesowi uczenia z
użyciem danych treningowych, dla których znana jest przynależność do poszczególnych klas.
W swojej podstawowej formie SVM jest liniowym klasyfikatorem binarnym, który po
rozszerzeniu o metodę miękkiego marginesu (tłum. autora, ang. soft margin) oraz metodę
jądra pozwala na klasyfikację liniowo nieseparowalnych danych w rozszerzonej przestrzeni
cech. Użycie funkcji decyzyjnych zwiększa możliwości klasyfikatorów SVM o możliwości
rozpoznania wielu klas.
Istotą metody SVM jest wyznaczenie
minimalizującej błąd generalizacji .
optymalnej
hiperpłaszczyzny
separującej,
3.1 Metoda SVM dla danych liniowo separowalnych
Załóżmy, że posiadamy M przykładów treningowych w przestrzeni m wymiarowej
xi (i = 1,...., M ) należących do dwóch możliwych klas oznaczonych jako yi = 1 to przykład
należy do klasy pierwszej oraz yi = −1 przykład należy do klasy drugiej. Hiperpłaszyczyzna
separująca może być określona wzorem D( x) = w x i + b
Zakładamy, że dane są liniowo separowalne czyli spełniony jest warunek:
T
y i ( w T x i + b) ≥ 1
(2.3.1.3)
Proces uczenia sprowadza się do minimalizacji funkcji celu
Q( w ) =
T
przy ograniczeniu y i (w x i + b) ≥ 1 .
9
1
w
2
2
(2.3.1.8)
3.2 Metoda SVM dla danych liniowo nieseparowalnych
W celu określenia klasyfikatora dla danych liniowo nieseparowalnych wproawdzono do
równania (2.3.1.3) dodatkową dodatnią zmienną ξ i ≥ 0 tzw zmienną luźną (ang. slack
variable).
y i (w T x i + b) ≥ 1 − ξ i dla i = 1,..,M
(2.3.2.1)
Oznacza to, że dopuszcza się aby poza wektorami leżącymi na hiperpłaszczyźnie
optymalnego marginesu znajdowały się przykłady danych uczących zwane ograniczonymi
wektorami podpierającymi (ang. bounded support vectors).
W celu regulacji wartości zmiennych ξ i , do funkcji celu wprowadza się człon karny w
M
postaci C ∑ ξ i , którego wpływ reguluje stała C (wzór 2.3.2.2) .
i =1
Q ( w , b, ξ ) =
1
w
2
2
M
+ C∑ξi
(2.3.2.2)
i =1
T
T
Gdzie ξ = (ξ1 ,.., ξ M ) oraz podlega ograniczeniu yi ( (w xi + b) ≥ 1 − ξ i oraz ξi ≥ 0 dla i = 1,..,M.
Stała C pozwala na kompromis pomiędzy maksymalizacją marginesu i minimalizacją błędu
klasyfikacji danych treningowych.
3.3 Wykorzystanie funkcji jądra
W przypadku danych liniowo nieseparowalnych pomimo wyznaczenia optymalnej
hiperpłaszyzny separującej zdolność klasyfikatora do generalizacji może nie być
wystarczająca. W celu zwiększenia złożoności zbioru funkcji separujących wykorzystuje się
funkcje jądra [Abe 2005]. Są to funkcje pozwalające na mapowanie przestrzeni wejściowej
do wielowymiarowej przestrzeni zwanej przestrzenia cech. Liniowa separacja następuje już
w przestrzeni cech dla rozszerzonej wartości wymiaru VC.
Dla nieliniowej funkcji wektorowej g(x) = ( g1 ( x),..., g l ( x)) mapującej m-wymiarowy wektor
wejściowy x na l-wymiarową przestrzeń cech, funkcja decyzyjna będzie miała postać:
T
D ( x ) = w T g ( x) + b
(2.3.3.1)
gdzie w jest l-wymiarowym wektorem , b – parametrem progowym
Zgodnie z twierdzeniem Mercera, jeśli symetryczna funkcja jądra K (x, x ′) spełnia warunek:
M
∑ hi h j K (x i , x j ) ≥ 0
i , j =1
10
(2.3.3.2)
dla każdego M , hi , x i gdzie
hi
przyjmuje wartości rzeczywiste to istnieje funkcja g(x) taka że
K (x, x ′) = g T (x)g(x ′)
(2.3.3.3)
Zaletą funkcji jądra w powyższej postaci iloczynu skalarnego, jest możliwość stosowania jej
zarówna w fazie uczenia jak i klasyfikacji, bez konieczności odwoływania się do często
bardzo rozbudowanej i wielowymiarowej funkcji g(x) .
3.4 Zalety metody SVM :
1) Maksymalizacja zdolności do generalizacji.
Podstawowa przewaga klasyfikatora SVM odnosząca się do teorii uczenia
związana ze zdolnością do maksymalizacji marginesu separującego. W przypadku,
gdy dane są liniowo separowalne oraz nawet przy niewielkiej ilości danych
treningowych, klasyfikator SVM posiada dobre właściwości klasyfikacji
nieznanych danych.
2) Brak minimów lokalnych.
Zadanie minimalizacji sformułowane jest w przypadku klasyfikatora SVM jako
problem programowania kwadratowego, w związku z tym posiada jedno dobrze
określone minimum globalne.
3) Odporność na dane odstające od większości danych.
Przy dużym C uzyskuje się lepszą skuteczność klasyfikacji danych treningowych
przy założeniu małej ilości danych odstających. Gdy wartość wsp. C ustalana jest
jako mała uzyskuje się zwykle gorszą jakość klasyfikacji danych treningowych,
dopuszcza się natomiast istnienie odstających danych, które mogą być
sklasyfikowane jako błędne. Zatem poprzez regulację wartości wsp. C można
zminimalizować wpływ danych określanych jako odstające.
3.5 Wady metody SVM:
1) Konieczność rozszerzania do problemu wieloklasowego
Ponieważ SVM jest klasyfikatorem binarnym, w przypadku danych należących do
więcej niż dwóch klas istnieje konieczność zastosowania technik rozszerzających
możliwości do klasyfikacji wieloklasowej przy użyciu rezultatów z odpowiednich
klasyfikatorów binarnych.
2) Długi czas uczenia
Ponieważ uczenie klasyfikatora SVM odbywa się poprzez rozwiązanie
odpowiedniego problemu dualnego, liczba zmiennych programowania
kwadratowego równa jest liczbie danych treningowych. Dla dużej ilości danych
treningowych rozwiązanie staje się bardzo czasochłonne z uwagi na ograniczenia
pamięci jak i szybkości procesora nawet dla aktualnych rozwiązań
technologicznych.
3) Konieczność doboru parametrów
Konieczność wyboru typu i parametrów jądra stwarza duże trudności związane z
testowaniem i wyborem najlepszego typu jądra oraz jego parametrów. Chociaż typ
jądra może być wybrany a priori na podstawie doświadczeń lub zaleceń
związanych ze specyfiką danych lub odpowiednią złożonością funkcji jądra, to
zestaw jego parametrów zwykle dobierany jest eksperymentalnie przy
zastosowaniu czasochłonnych metod statystycznych.
11
4 Cele i tezy pracy
4.1 Cele pracy
1) Opracowanie metody SVM predykcji podstawowych klas strukturalnych domen
białkowych przy wykorzystaniu cech kompozycji aminokwasów.
2) Opracowanie metod ekstrakcji cech odzwierciedlających długość sekwencji oraz efekt
kolejności opartej o fizykochemiczne właściwości aminokwasów.
3) Opracowanie metody selekcji cech pozwalającej na wyszczególnienie cech istotnych.
4.2 Tezy pracy
•
Teza 1: Zastosowanie metody SVM pozwala na dokładniejszą predykcję klas
strukturalnych niż wykorzystywane metody oparte na minimalnej odległości.
•
Teza 2: Ekstrakcja cechy długości sekwencji oraz cech opartych o efekt
kolejności na bazie właściwości fizykochemicznych aminokwasów pozwala na
podniesienie dokładności predykcji klas strukturalnych.
•
Teza 3: Selekcja cech istotnych pozwala na ograniczenie ilości i dobór
odpowiednich cech bez straty dokładności klasyfikacji.
4.3 Dobór danych
Wprowadzono szereg uproszczonych i różnych kryteriów przynależności do klasy opartych
na procentowym udziale struktur α i β. Jednak dopiero wprowadzone przez Murzina nieco
inne przybliżenie problemu dało podstawy do zunifikowania i sklasyfikowania znanych
struktur domen białkowych w bazie SCOP (Structural Classification Of Protein) [Murzin
1995]. Murzin zaproponował aby podstawową jednostką klasyfikacji była domena a nie jak
dotychczas cała struktura białka a klasyfikacja oparta została o tzw. ewolucyjne
pokrewieństwo oraz o pewne zasady tworzenia struktur 3-D. Baza danych SCOP zawiera w
sobie klasyfikację wszystkich aktualnie występujących w bazie PDB białek, oraz wiele
publikowanych niedostępnych w bazie PDB [Hubbard 1998]. Baza SCOP dodatkowo posiada
szczegółowy opis strukturalnej i tzw. ewolucyjnej zależności białek stanowiąc aktualnie
najbardziej kompletną i wiarygodną bazę dla celów predykcji klas strukturalnych [Chou
1998].
Wcześniejsze implementacje wykorzystywały dane, których niewielka liczba jak i wysoka
redundancja nie pozwalały na wiarygodne określenie uogólnionego modelu klasyfikacji oraz
jego dokładności (tutaj rzędu 90%) [Chou 1995, Zhou 1998]. Bardziej wiarygodne rezultaty
choć już nie tak dobre, zostały osiągnięte przy użyciu znacznie większej liczby danych z bazy
SCOP.
12
4.4 Ekstrakcja cech
Konwencjonalna kompozycja aminokwasów na podstawie, której dokonuje się klasyfikacji
strukturalnej białek zawiera 20 komponentów, dyskretnych wartości, z których każda
odzwierciedla częstotliwość występowania jednego z 20 aminokwasów w białkach [Chou
1995, Chou 1995a].
Kompozycja pseudo-aminokwasów pozwala na rozszerzenie wektora cech o wartości
pozwalające na odzwierciedlenie efektu kolejności sekwencji [Chou 2001, Chou 2003a, Lin
2008, Zhang 2008, Chou 2009, Chou 2005, Chou 2004, Chou 2005a]. Koncepcja pseudoaminokwasów zakłada rozszerzenie konwencjonalnych komponentów do komponentów
zawierających informację o kolejności aminokwasów odpowiednio co drugiego, co trzeciego
itd. uwzględniając pewne zależności a więc i oddziaływania pomiędzy nimi na podstawie ich
właściwości biochemicznych.
Klasyfikacja na poszczególne klasy strukturalne odbywa się jedynie na podstawie udziału
dwudziestu aminokwasów wchodzących w skład białka tj. członu AAC jak i korelacji
pomiędzy cechami biochemicznymi oddalonych o pewną wartość aminokwasów. Mając do
dyspozycji dużą bazę zawierającej domeny o różnych długościach łańcucha polipeptydu
warto postawić pytanie o wpływ długości łańcucha na wynik klasyfikacji. W tym celu dodana
została wartość 1/n cechy uwzględniającej długość domeny białkowej do członu AAC
Ostatecznie badane cechy uzyskały kształt pokazany na rysunku 4.4.2.
Rysunek 4.4.2 Układ zastosowanych cech: 1/n – cecha odzwierciedlająca długość sekwencji, AAC – cechy
kompozycji aminokwasów (udziału reszt w łańcuchu polipeptydu), PSE- cechy związane z korelacją
właściwości biochemicznych znajdujących się w sąsiedztwie co 1,2,3,4,... reszt
1/n jest 21 cechą rozkładu AAC, którą można zinterpretować jako 21 typ aminokwasu,
którego częstość występowania jest odwrotnie proporcjonalna do długości łańcucha domeny
białkowej. PSE to komponenty pseudo-aminokwasów, których udział w stosunku do
pozostałych cech określa odpowiedni współczynnik wagowy.
4.5 Selekcja cech
Zmniejszenie wymiaru danych wejściowych pozwala na zredukowanie zbioru cech do
optymalnego podzbioru cech pozwalającego na uzyskanie najlepszej dokładności
klasyfikatora i (lub) wyraźną poprawę jego możliwości obliczeniowych [Kohavi 1997]. Zbyt
duży wymiar zmiennych może być przyczyną przeuczenia klasyfikatora przekładający się na
wzrost wymiaru VC i na wzrost ryzyka gwarantowanego [Guyon 2002,Guyon 1992].
Ekstrakcja cech przy pomocy metody PCA szeroko stosowanej do wstępnej redukcji
wymiaru zmiennych poprzez rzutowanie cech na składowe główne, gdzie nowe cechy są
liniową kombinacją oryginalnych cech, powoduje utratę przejrzystej informacji dotyczącej
nierzadko interesującego nas wpływu oryginalnych cech [Guyon 2002]. W takim przypadku
13
stosuje się selekcję cech, w celu określenia cech istotnych [Kohavi 1997]. Celem jest
znalezienie cech, które wpływają na wynik klasyfikacji również w kontekście innych cech jak
i eliminacja cech, które ze względu na występującą redundancję pozostają istotne, lecz nie są
użyteczne [Guyon 2002].
Z uwagi na niewielką ilość cech w pracy wykorzystano metodę selekcji przy pomocy Crossvalidation danych treningowych oraz metodę rankingu na podstawie dokładności klasyfikacji
wydzielonych danych walidacyjnych. Wybrano metodę eliminacji cech dla określonego
wcześniej modelu klasyfikatora. Inną zastosowaną metodą jest metoda eliminacji cech przy
pomocy klasyfikatora RFE-SVM.
WEJŚCIE:
1) Zbiór cech uporządkowanych w rankingu R=[]
2) Wybrany zestaw wszystkich cech W=[1,...,m]
1) Trenuj klasyfikator SVM dla zestawu cech W.
2) Oblicz wagi rankingu cech c f dla zestawu cech W
Sprawdzian
krzyżowy
Ocena na podstawie danych
walidacyjnych
RFE
Wybierz cechę o najmniejszej wartości wagi
c = arg min f c f
1) Dodaj cechę na początek rankingu R=[c,R]
2) Usuń cechę z zestawu cech W
Nie
W=[]
WYJŚCIE :
Lista wszystkich cech uporządkowanych w
rankingu R
Rysunek 4.5.1 Algorytm selekcji cech.
14
5 Wybrane wyniki badań
5.1 Porównanie predykcji klas strukturalnych uzyskanych metodami minimalnoodległościowymi oraz metodą SVM z użyciem cech komponentów aminokwasów
(AAC)
W celu porównania powyższych metod oraz zastosowanej metody SVM wykorzystano
najnowsze dane bazy SCOP (wydanie 1.75). Wybrano 7702 domeny poniżej 30%
podobieństwa sekwencji. Dokonano losowego podziału danych na treningowe i testowe w
taki sposób, aby zarówno w danych treningowych jak i testowych wystąpił podobny rozkład
długości jak i ilości domen w poszczególnych klasach. Przeprowadzono klasyfikację dla
metod DH, DE, CC oraz SVM. Parametry modelu SVM dobrano według metody grid, za
kryterium przyjęto współczynnik sprawności dla 10 krotnego sprawdzianu krzyżowego (cross
validation – 10-CV). Uzyskano wartość dokładności współczynnika dla metody grid-CV
równą 55% dla wartości C=216 i g=2-14 (rys. 5.1.1).
Rysunek 5.1.1 Wykres konturowy uzyskany metodą grid, dla klasyfikatora SVM przy użyciu cech AAC
Podczas wyboru modelu i treningu klasyfikatora SVM wykorzystano jedynie zbiór
treningowy. Za najbardziej wiarygodną wartość predykcji klas nieznanych danych przy
pomocy SVM należy przyjąć współczynnik dokładności klasyfikacji danych testowych tj.
56%. Dla porównania dla tych samych danych testowych uzyskano dokładność dla
algorytmów DH, DE, CC odpowiednio 48%, 50%, 53%. Dla danych treningowych
odpowiednio 46%, 49%, 56% oraz 60% dla klasyfikacji SVM.
Metoda
Dokładność (%)
DH
DE
48
CC
50
15
SVM
53
56
Tabela 5.1.1 Porównanie dokładności klasyfikacji przy pomocy metod minimalnej odległości
oraz SVM. W tabeli podano współczynniki dokładności klasyfikacji dla danych testowych.
5.2 Predykcja klas strukturalnych domen białkowych przy pomocy SVM dla
rozszerzonych cech komponentów aminokwasów
Dobór metody i jej parametrów jest istotny dla dokładności klasyfikacji z punktu widzenia
najbardziej odpowiedniego modelu separacji danych zapewniającego jak najlepszą zdolność
do predykcji klas nieznanych danych. Jednak równie ważnym o ile nie najważniejszym
elementem pozwalającym na uzyskanie klasyfikatora o jak największej dokładności, poza
właściwym doborem przykładów uczących jak i testowych, jest dobór odpowiednich cech
reprezentujących czynniki posiadające wpływ na dokładność klasyfikacji.
5.2.1
Cecha reprezentująca długość łańcucha domeny białkowej
W niniejszej pracy przeprowadzono testy dla dodatkowej cechy reprezentującej długość
łańcucha białkowego (1/n) oraz cech opartych o efekt kolejności sekwencji na bazie
właściwości aminokwasów (PseAA).
Rysunek 5.3.1.1 Wykres konturowy uzyskany metodą grid, dla klasyfikatora SVM przy użyciu cech
AAC+1/n.
5.2.2
Wpływ cech reprezentujących efekt kolejności aminokwasów łańcucha domeny
białkowej
Najlepszą dokładność klasyfikacji dla dodatkowych cech PseAA uzyskano dla jednego z
typów cech pseudo-aminokwasów wraz z uwzględnieniem cechy 1/n.
16
Rysunek 5.3.2.1 Wykres konturowy uzyskany metodą grid, dla klasyfikatora SVM przy użyciu cech PSE
Typ3+1/n.
Porównując jakość klasyfikacji dla danych testowych i różnych zestawów cech tj. AAC,
AAC+1/n oraz PSE Typ3+1/n (PseAA) uzyskano dokładność odpowiednio 56%, 59% , 62%.
Dla danych treningowych odpowiednio 60%, 62% oraz 67%. Najlepszą dokładność predykcji
klas nieznanych danych określa współczynnik równy 62% dla danych testowych i zestawu
cech PSE Typ3+1/n. (tab. 5.3.2.1)
Zestaw Cech
Dokładność (%)
AAC
56
AAC+1/n Pse Typ3 +1/n
59
62
Tabela 5.3.2.1 Porównanie dokładności klasyfikacji SVM dla różnych zestawów cech.
5.3 Selekcja cech istotnych
W celu eliminacji cech, które nie mają istotnego wpływu lub mają negatywny wpływ na
dokładność klasyfikacji, przeprowadza się selekcję cech. Dzięki redukcji cech uzyskuje się
redukcję ilości składowanych danych, lepszą wydajność przetwarzania oraz lepsze
zrozumienie wpływu cech na dokładność klasyfikacji.
Zgodnie z założeniami zastosowano trzy metody redukcji cech.
1) Nieliniową wieloklasową metodę RFE.
2) Metodę Cross Validation (CV).
3) Redukcję przy pomocy kryterium dokładności klasyfikacji wydzielonych danych
walidacyjnych.
17
Cross Validation dla danych treningowych
Met. CV
Met. Valid
Met. RFE
70,00
Dokładność%
65,00
60,00
55,00
50,00
45,00
40,00
35,00
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
30,00
L. cech
Wykres 5.4.1 Wpływu selekcji cech na współczynnik sprawdzianu krzyżowego dla danych
treningowych i jednego ze zbioru cech pseudo aminokwasów (PseAA). Metody: CV,
Walidacyjna, RFE zostały opisane w punkcie 4.5.
Redukcji poddano zestaw cech o uzyskanej najlepszej dokładności klasyfikacji (PseAA) oraz
zastosowany klasyfikator SVM.
Jako podstawowe kryterium przyjęto współczynnik dokładności CV dla danych
treningowych. Najlepsze rezultaty uzyskano przy użyciu metody CV (wyk. 5.4.1 ).
Najlepszą wartość współczynnika CV uzyskano dla 72 cech i wynosiła ona 63,87 % przy
dokładność klasyfikacji dla danych testowych wynoszącej 62,07 % (tab. 5.4.1).
Zakładając maksymalną redukcję cech przy nie mniejszej dokładności współczynnika
CV niż przed redukcją, można dokonać eliminacji do 30 cech. Wartość współczynnika CV
wynosi 62,57 % przy dokładności klasyfikacji dla danych testowych wynoszącej 61,79 %.
Number of
features
Classification
precision for test
CV (%) for
data (%)
training data
111
63
62
72
64
62
30
63
62
Tabela 5.4.1 Dokładność klasyfikacji dla grup wyselekcjonowanych cech: wszystkich 111 cech, 72 cech o
najlepszym wsp. CV oraz 30 cech o wsp. CV jak przed selekcją.
18
Literatura
[Shawn 2002] Peptides and Proteins , Tutorial Chemistry Texts 15, Shawn Doonan , University of East London,
Royal Society of Chemistry 2002.
[Hart 1999] Chemia organiczna , Krótki kurs, Harold Hart, Leslie E. Craine, David J. Hart , Wydawnictwo
Lekarskie PZWL 1999.
[Szymański 2007] Postępy Biochemii, vol. 53, nr 4, 2007 (http://www.postepybiochemii.pl/vol53-4.htm), Maciej
Szymański, Jan Barciszewski, Instytut Chemii Bioorganicznej Polskiej Akademii Nauk .
[Buxbaum 2007] Fundamentals of Protein Structure and Functions, Engelbert Buxbaum, Springer 2007.
[Solomon 2007] Biologia, wg VII wydania amerykańskiego, Eldra P.Solomon , Linda R. Berg, Diana W. Martin,
MULTICO Oficyna Wydawnicza, Warszawa 2007.
[Voet 2004] Biochemistry, Volume One, Biomolecules, Mechanisms of Enzyme Action, and Metabolism, 3rd
Edition, Donald Voet , Judith G. Voet, Wiley 2004, John Wiley & Sons 2004.
[Hames 2002] Biochemia, Krótkie wykłady, B.D. Hames , N.M. Hooper, Wydawnictwo Naukowe PWN,
Warszawa 2007.
[Ramachandran Plots] Ramachandran Plots. Amino Acid Configuration in Proteins, Brak autora,
http://www.greeley.org/~hod/papers/Unsorted/Ramachandran.doc.pdf.
[Abe 2005] Support Vector Machines for Pattern Classification, Shigeo Abe, Springer 2005.
[Osuna 1997] Support Vector Machines Training and Applications , Edgar E. Osuna, Robert Freund and
Federico Girosi, A.I. Memo No. 1602, C.B.C.L Paper No. 144, 1997.
Applications
[Vapnik 1995] The Nature of Statistical Learning Theory, Vladimir N. Vapnik, Second Edition, Springer 1995.
[Fradkin 2005] Support Vector Machines for Classification, Dmitriy Fradkin , Ilya Muchnik,, IMACS Series in
Discrete Mathematics and Theoretical Computer Science 2005.
[Chang 2011] LIBSVM: a Library for Support Vector Machines , Chih-Chung Chang and Chih-Jen Lin,
Department of Computer Science National Taiwan University, Taipei, Taiwan
Email: [email protected].
[Guyon 2002] Gene Selection for Cancer Classification using Support Vector Machines, Isabelle Guyon, Jason
Weston, Stephen Barnhill, Vladimir Vapnik, Machine Learning, 46, 389–422, 2002.
[Zhou 2007] MSVM-RFE: extensions of SVM-RFE for multiclass gene selection on DNA microarray data, Xin
Zhou, David P. Tuck, Department of Pathology, Yale University School of Medicine, New Haven, Connecticut
2007.
[Guyon 2006] An Introduction to Feature Extraction, Feature Extraction. Foundations and Applications.
Isabelle Guyon, Andre Elisseeff , Springer 2006.
[Kohavi 1997] Wrappers for Feature Subset Selection, Ron Kohavi, George H. John , Artificial Intelligence,
Volume 97, Issues 1-2, December 1997, Pages 273-324.
[Guyon 1992] Structural Risk Minimization for Character Recognition, I. Guyon, V. Vapnik, B. Boser, L.
Bottou, S.A. Solla, AT&T Bell Laboratories, Holmdel, USA 1992.
[LeCun 1990] Optimal Brain Damage, Yann Le Cun, John S. Denker, Sara A. Solla, AT&T Bell Laboratories,
Holmdel, N. Y. 1990.
19
[Lin 2008] Prediction of Subcellular Localization of Apoptosis Protein Using Chou’s Pseudo Amino Acid
Composition, Hao Lin, Hao Wang , Hui Ding, Ying-Li Chen, Qian-Zhong Li. Acta Biotheoretica , Volume 57,
Number 3, 321-330,
[Shen 2006] Ensemble classifier for protein fold pattern recognition, Hong-Bin Shen, Kuo-Chen Chou.
Bioinformatics (2006) 22 (14): 1717-1722.
[Chou 2001] Prediction of Protein Cellular Attributes Using Pseudo-Amino Acid Composition, Kuo-Chen Chou.
Proteins: Structure, Function, and Bioinformatics, Volume 43 Issue 3 pages 246-255, 2001.
[Chou 2004] Predicting Subcellular Localization of Proteins by Hybridizing Functional Domain Composition
and Pseudo-Amino Acid Composition, Kuo-Chen Chou, Yu-Dong Cai., Journal of Cellular Biochemistry (2004),
Volume: 91, Issue: 6, Pages: 1197-1203.
[Chou 2003] Prediction and Classification of Protein Subcellular Location-Sequence-Order Effect and Pseudo
Amino Acid Composition, Kuo-Chen Chou, Yu-Dong Cai, Journal of Cellular Biochemistry (2003),Volume: 90,
Issue: 6, Pages: 1250-1260.
[Cai 2003a] Support Vector Machines for Predicting Membrane Protein Types by
Using Functional Domain Composition, Yu-Dong Cai, Guo-Ping Zhou,y, Kuo-Chen Chou, Biophysical Journal,
Volume 84, Issue 5, 3257-3263, 1 May 2003.
[Chou 1999] Using Pair-Coupled Amino Acid Composition to Predict Protein Secondary Structure Content ,
Kuo-Chen Chou, Journal of Protein Chemistry Volume 18, Number 4, 473-480,.
[Shen 2007] PseAAC: A flexible web server for generating various kinds of protein pseudo amino acid
composition . Hong-Bin Shen a,b, Kuo-Chen Chou. Analytical Biochemistry 373 (2008) 386–388
[Chou 1995] A novel approach to predicting protein structural classes in a (20–1)-D amino acid composition
space, Kuo-Chen Chou . Proteins. 1995 Apr;21(4):319-44.
[Zerrin 2003] Computational Approaches to Protein Structure Prediction. Zerrin I. . Submitted to the Graduate
School of Engineering and Natural Sciences in partial fulfillment of the requirements for the degree of Master of
Science Sabancı University Spring 2003
[Chou 2005] Prediction of protease types in a hybridization space, Kuo-Chen Chou ,Yu-Dong Cai, Biochemical
and Biophysical Research Communications 339 (2006) 1015–1020.
[Chou 2004a] Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes, Kuo-Chen
Chou, Bioinformatics (2005) 21 (1): 10-19.
[Chou 2009] Pseudo Amino Acid Composition and its Applications in Bioinformatics, Proteomics and System
Biology, Kuo-Chen Chou, Current Proteomics, 2009, 6, 262-274.
[Chou 2005a] Progress in Protein Structural Class Prediction and its Impact to Bioinformatics and Proteomics,
Current Protein and Peptide Science, Volume 6, Number 5, October 2005 , pp. 423-436(14), Kuo-Chen Chou.
[Chou 1995a] Prediction of Protein Structural Classes. Kuo-Chen Chou, Chung-Ting Zhang, Critical Reviews
in Biochemistry and Molecular Biology, 30(4);275-349 (1995).
[Esmaeili 2009] Using the concept of Chou’s pseudo amino acid composition for risk type prediction of human
papillomaviruses, Maryam Esmaeili, Journal of Theoretical Biology
Volume 263, Issue 2, 21 March 2010, Pages 203-209, Hassan Mohabatkar , Sasan Mohsenzadeh.
[Zhang 2008] Predicting Lipase Types by Improved Chou’s Pseudo-Amino Acid Composition, Protein and
Peptide Letters (2008) Volume: 15, Issue: 10, Pages: 1132-1137 ,Guang-Ya Zhang, Hong-Chun Li, Jia-Qiang
Gao, Bai-Shan Fang.
[Chou 2003a] Predicting Protein Quaternary Structure by Pseudo AminoAcid Composition, Kuo-Chen Chou,
Yu-Dong Cai. PROTEINS: Structure, Function, and Genetics 53:282–289 (2003)
20
[Jankowski 1999] Ontogeniczne sieci neuronowe w zastosowaniu do klasyfikacji danych medycznych, Norbert
Jankowski. Praca doktorska pod kierunkiem prof. Włodzisława Ducha, Katedra Metod Komputerowych
Uniwersytetu Mikołaja Kopernika, Torun´ 1999
[Stateczny 2002] Sztuczne Sieci Neuronowe w Rozpoznawaniu Obiektów Morskich, Andrzej Stateczny, Tomasz
Praczyk.Gdańkie Towarzystwo Naukowe 2002
[Tanford 1962] Contribution of Hydrophobic Interactions to the Stability of the Globular Conformation of
Proteins, Charles Tanford. J. Am. Chem. Soc., 1962, 84 (22), pp 4240–4247
[Hopp 1981] Prediction of protein antigenic determinants from amino acid sequences (hydrophilicity
analysis/protein conformation) T.P. Hopp, K. R. Woods. Proc Natl Acad Sci U S A. 1981 Jun;78(6):3824-8.
[Dasgupta AAI] Amino Acids I. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur. http://classle.net/bookpage/core-science-biochemistry-i .
[Dasgupta AAII] Amino Acids II. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur. http://classle.net/bookpage/core-science-biochemistry-i .
[Dasgupta PSI] Protein Structure I. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur. http://classle.net/bookpage/core-science-biochemistry-i .
[Dasgupta PSII] Protein Structure II. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur.
http://classle.net/bookpage/core-science-biochemistry-i .
[Dasgupta PSIII] Protein Structure III. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur. http://classle.net/bookpage/core-science-biochemistry-i
[Dasgupta PS4] Protein Structure 4. Core Science - Biochemistry I, Lecture Series on BioChemistry I by
Prof.S.Dasgupta, Dept of Chemistry, IIT Kharagpur.
http://classle.net/bookpage/core-science-biochemistry-i
[Koolman 2005] Color Atlas of Biochemistry, J. Koolman K.H.Roehm. Second edition, revised and enlarged,
Thieme Stuttgart – New York 2005
[HO 2003] Revisiting the Ramachandran plot: Hard-sphere repulsion, electrostatics, and H-bonding in the αhelix. BOSCO K. HO, ANNICK THOMAS, ROBERT BRASSEUR. Protein Sci. 2003 November; 12(11):
2508–2522
[Chou 2000] Prediction of Tight Turns and Their Types in Proteins, Kuo-Chen Chou. Analytical Biochemistry
286, 1–16 (2000)
[Cai 2003] Prediction of β-turns with learning machines, Yu-Dong Cai, Xiao-Jun Liu, Yi-Xue Li, Xue-biao Xu,
Kuo-Chen Chou. Peptides ,Volume 24, Issue 5, May 2003, Pages 665-669
[Chou 1997] Prediction of β-turns. Kuo-Chen Chou. The Journal of Peptide Research
Volume 49, Issue 2, pages 120–144, February 1997.
[Zhang 1996] Prediction of β-turns in Proteins by 1-4 and 2-3 Correlation Model, Chung-Ting Zhang, KuoChen Chou. John Wiley & Sons, Inc. Biopoly 41:673-702, 1997
[Chou 1997a] Prediction and Classification of α-Turn Types, Kuo-Chen Chou. John Wiley & Sons, Inc.
Biopoly 42:837-853, 1997 .
[Rajashankar 1996] π-Turns in proteins and peptides: Classification, conformation, occurrence, hydration and
sequence K.R. RAJASHANKAR AND S. RAMAKUMAR. Protein Science (1996), 5:932-946. Cambridge
University Press. Printed in the USA
21
[Chatterjee 2007] Expanding the polypeptide backbone: hydrogen-bonded conformations in hybrid polypeptides
containing the higher homologues of α-amino acids, Sunanda Chatterjee, Rituparna Sinha Roy, P. Balaram. J. R.
Soc. Interface 22 August 2007 vol. 4 no. 15 587-606
[Cai 2002] Support Vector Machine for predicting α-turn types, Yu-Dong Cai, Kai-Yan Feng, Yi-Xue Li , KuoChen Chou. Peptides 24 (2003) 629–630
[Reid 2000] Peptide and Protein Drug Analysis. Ronald Reid, James Swarbrick. Informa HealthCare; 1st
edition (December 15, 1999)
[Chothia 1997] PROTEIN FOLDS IN THE ALL-α AND ALL-β CLASSES, Cyrus Chothia, Tim Hubard, Steven
Brenner, Hugh Barns, Alexey Murzin. Annu. Rev. Biophys. Biomol. Struct. 1997. 26:597–627 .
[Branden 1999] Introduction to Protein Structure, Carl Branden, John Tooze. Second Edition, Published by
Garland Publishing, Inc. 19 Union Square West, New York 1999.
[Lesk 2001] Introduction to Protein Architecture: The Structural Biology of Proteins, Arthur M. Lesk. Oxford
University Press, USA; 1 edition (2001).
[Chou 1991] Energetic Approach to the Folding of α/β Barrels, Kuo-Chen Chou, Louis Carlacci. PROTEINS:
Structure, Function and Genetics, 1991, 9, 280-295 .
[Chothia 1990] THE CLASSIFICATION AND ORIGINS OF PROTEIN FOLDING PATTERNS. Cyrus Chothia,
Alexei V. Finkelstein. Annu. Rev. Biochem. 1990. 59:1007-39 .
[Chothia 1977] Structure of proteins: Packing of a-helices and pleated sheets, CYRUS CHOTHIA, MICHAEL
LEVITT, DOUGLAS RICHARDSON. Proc. Nati. Acad. Sci. USA
Vol. 74, No. 10, pp. 4130-4134, October 1977 Chemistry .
[Chothia 1989] Polyhedra for helical proteins. Cyrus Chothia. Nature. Vol. 337 19 January 1989.
[Murzin 1994] Principles Determining the Structure of β-Sheet Barrels in Proteins. Alex G. Murzin, Arthur M.
Lesk, Cyrus Chothia. J. Mol. Biol. (1994) 236, 1369-1381.
[Chothia 1984] PRINCIPLES THAT DETERMINE THE STRUCTURE OF PROTEINS. Cyrus Chothia. Ann.
Rev. Biochem. 1984.53: 537-72.
[Chothia 1981] Helix to Helix Packing in Proteins. CYRUS CHOTHIA, MICHAEL LEVITT,DOUGLAS
WHAILDSON. ,J. Mol. Biol. (1981) 145, 215-250.
[Janin 1980] Packing of α-Helices onto β-Pleated Sheets and the Anatomy of α/β Proteins
JOEL JANIN , CYRUS CHOTHIA. .J. Mol. Biol. (1980) 143, 95-128.
[Levitt 1976] Structural patterns in globular proteins. Michael Levitt, Cyrus Chothia. Nature, vol. 261, No.
5561, pp. 552-558, June 17, 1976.
[Chothia 1982] Orthogonal Packing of, β-Pleated Sheets in Proteins, Cyrus Chothia, Joel Janin. Biochemistry
1982, 21, 3955-3965.
[Wang 2005] Support Vector Machines: Theory and Applications, Lipo Wang. Springer 2005.
[Burges 1998] A Tutorial on Support Vector Machines for Pattern Recognition, CHRISTOPHER J.C. BURGES.
Data Mining and Knowledge Discovery, 2, 121–167 (1998).
[Boser 1992] A Training Algorithm for Optimal Margin Classiers, Bernhard E. Boser, Isabelle M. Guyon,
Vladimir N. Vapnik. COLT '92 Proceedings of the fifth annual workshop on Computational learning theory,
New York, NY, USA ©1992..
22
[Janeczek 2008] Analiza wiarygodności danych z wykorzystaniem maszyn wektorów podpierających SVM ,
Bartosz Janeczek. Praca dyplomowa magisterska, Politechnika Warszawska Wydział Elektroniki i Technik
Informacyjnych, Instytut Informatyki. 2007/2008, Opiekun dr inż. Roman Podraza.
[Aczel 2000] Statystyka w zarządzaniu, Amir D, Aczel. PWN, Warszawa 2000.
[Prevelige 1989] Prediction of Protein Structure and the Principles of Protein Conformation. G. D. Fasman
(Editor). Springer; 1 edition (October 31, 1989). Chapter 9: Chou-Fasman Prediction of the Secondary
Structure of Proteins The Chou-Fasman-revelige Algorithm, Peter Prevelige, Jr., and Gerald D. Fasman..
[Edholm 2010] The Chou-Fasman method for predicting secondary structure, Olle Edholm. Alba Nova
University Center , KTH - Theoretica Physics , SE-106 91 Stockholm - Sweden, [email protected] .
[Singh 2000] COS551 Intro. to Computational Biology, Mona Singh.
http://www.cs.princeton.edu/~mona/Lecture/sec-structure.pdf .
[Zhou 1998] An Intriguing Controversy over Protein Structural Class Prediction, Guo-Ping Zhou. Journal of
Protein Chemistry, Vol. 17, No. 8, 1998.
[Gu 2008] Protein structural class prediction based on an improved statistical strategy, Fei Gu, Hang Chen, Jun
Ni. BMC Bioinformatics 2008, 9 (Suppl 6):S5.
[Hsu 2010] A Practical Guide to Support Vector Classification, Chih-Wei Hsu, Chih Chung Chang, Chih-Jen
Lin. Departament of Computer Science 2010, http://www.csie.ntu.edu.tw/~cjlin ..
[Hochreiter 2007] Bioinformatics III. Structural Bioinformatics and Genome Analysis. Sepp Hochreiter. Lecture
Notes, Institute of Bioinformatics , Johannes Kepler University Linz, A-4040 Linz, Austria,
http://www.bioinf.jku.at..
[Trojanowski 1977] Biochemia dla Biologów. Jerzy Trojanowski. PWN Warszawa 1977.
[Eisenhaber 1995] Protein Structure Prediction: Recognition of Primary, Secondary, and Tertiary Structural
Features from Amino Acid Sequence. Frank Eisenhaber, Bengt Persson, Patrick Argos. Critical Reviews in
Biochemistry and Molecular Biology, 30(1):1-94 (1995)..
[Chou 1998] Domain structural class prediction, Kuo-Chen Chou1 and Gerald M.Maggiora. Protein
Engineering vol.11 no.7 pp.523–538, 1998.
[Hubbard 1998] SCOP, Structural Classification of Proteins Database: Applications to Evaluation of the
Effectiveness of Sequence Alignment Methods and Statistics of Protein Structural Data, Tim J. P. Hubbard, Bart
Ailey, Steven E. Brenner, Alexey G. Murzin, Cyrus Chothia. Acta Cryst. (1998). D54, 1147-1154.
[Hubbard 1999] SCOP, Structural Classification of Proteins Database, Tim J. P. Hubbard, Bart Ailey, Steven E.
Brenner, Alexey G. Murzin, Cyrus Chothia. Nucleid Acids Research, 1999, Vol. 27, No. 1.
[Murzin 1995] SCOP: A Structural Classification of Proteins Database for the Investigation of Sequences and
Structures Alexey G. Murzin, Steven E. Brenner, Tim Hubbard and Cyrus Chothia. J. Mol. Biol. (1995) 247,
536–540 .
[Chandonia 2004] The ASTRAL Compendium in 2004. John-Marc Chandonia, Gary Hon, Nigel S. Walker,
Loredana Lo Conte, Patrice Koehl, Michael Levitt, Steven E. Brenner. Nucleic Acids Research, 2004, Vol. 32,
Database issue D189-D192.
[Liu 2008] Classification and feature selection algorithms for multi-class CGH data, Jun Liu, Sanjay Ranka,
Tamer Kahveci. Bioinformatics , Volume 24 Issue 13, July 2008.
[Guyon 2003] An Introduction to Variable and Feature Selection, Isabelle Guyon, Andr´e Elisseeff. Journal of
Machine Learning Research 3 (2003) 1157-1182 .
23
[Shieh 2008] Multiclass SVM-RFE for product form feature selection, Meng-Dar Shieh, Chih-Chieh Yang.
Expert Systems with Applications Volume 35, Issues 1-2, July-August 2008, Pages 531-541.
[Guyon 2007] Feature selection and causal discovery fundamentals and applications, Isabelle Guyon.
http://langtech.jrc.it/mmdss2007/htdocs/Presentations/Docs/MMDSS_Guyon.pdf .
[Oza 1999] Dimensionality Reduction Through Classifier Ensembles, Nikunj C. Oza, Kagan Turner. Technical
Report NASA-ARC-IC-1999-126, NASA Ames Research Center, 1999.
[Guyon 2008] Mining Massive Data Sets for Security: Advances in Data Mining, Search, Social Networks and
Text Mining, and their Applications to Security, F. Fogelman-Soulie (Author, Editor), D. Perrotta (Editor), J.
Piskorski (Editor), R. Steinberger (Editor). IOS Press (December 15, 2008). Chapter : Practical Feature
Selection: from Correlation to Causality, Isabelle Guyon.
[Twardowski 2005] Numeryczne metody obliczeń technicznych . Wykład VII, Wartości i wektory własne.
Wartości osobliwe i dekompozycja SVD, Tomasz Twardowski.
http://galaxy.uci.agh.edu.pl/~ttward/numer/Warto%9Cci%20i%20wektory%20w%B3asne.pdf
[Dutkowski 2007] Eksploracyjna analiza danych. Metody rzutowania: analiza składowych głównych oraz
skalowanie wielowymiarowe. Janusz Dutkowski. http://www.mimuw.edu.pl/~aniag/SADM/pca.pdf.
[The Biochemistry Questions] The Biochemistry Questions
http://biochemistryquestions.wordpress.com/2008/10/02/secondary-structure-of-proteins/.
[Muñoz 1996] Analysis of the effect of local interactions on protein stability. Victor Muńoz, Philippe Cronet,
Eva López-Hernández and Luis Serrano. Folding and Design Volume 1, Issue 3, June 1996, Pages 167-178.
[Muñoz 1996a] Local versus nonlocal interactions in protein folding and stability - an experimentalist’s point of
view, Victor Muñoz, Luis Serrano. Folding and Design Volume 1, Issue 4, August 1996, Pages R71-R77.
[Overview Beta] Overview of Beta-Pleated Sheet Secondary Structure. http://mcdbwebarchive.mcdb.ucsb.edu/sears/biochemistry/.
[Overview Alpha] Alpha-Helix: Overview of Secondary Structure. http://mcdbwebarchive.mcdb.ucsb.edu/sears/biochemistry/..
24