TERMODYNAMIKA Termodynamika jest to dział nauk

TERMODYNAMIKA
Termodynamika jest to dział nauk przyrodniczych zajmujący się własnościami
energetycznymi ciał. Przy badaniu i objaśnianiu własności układów fizycznych
termodynamika posługuje się pojęciami makroskopowymi bez wnikania w obraz
mikroskopowy zjawisk. U podstaw termodynamiki leżą zasady termodynamiki otrzymane w
wyniku uogólnienia obserwacji doświadczalnych.
Termodynamika rozważa zbiory ciał, które nazywane są układami
termodynamicznymi. Układ jest w stanie równowagi termodynamicznej jeśli posiada dobrze
określone parametry termodynamiczne. Parametry termodynamiczne takie jak temperatura,
ciśnienie, objętość czy liczba cząstek układu określają stan układu. W równowadze
termodynamicznej parametry te są stałe w dowolnie długim czasie ( mogą, ściśle mówiąc,
podlegać niewielkim fluktuacjom ) przy niezmiennych warunkach zewnętrznych. Proces
przechodzenia układu z stanu nierównowagowego do równowagowego nazywa się relaksacją.
Przejście układu z jednego stanu do drugiego nazywamy przemianą termodynamiczną. Jeśli
przemiana składa się z ciągłego zbioru kolejnych stanów równowagi to nosi nazwę
równowagowej – zakłada się , że taka przemiana może zachodzić także w odwrotnym
kierunku.
Ważnym pojęciem termodynamiki jest energia wewnętrzna. Energia wewnętrzna jest
równa całkowitej energii układu. Składa się z energii kinetycznej poszczególnych składników
układu ( np. cząsteczek gazu ) i energii oddziaływań wzajemnych składników, a także z
energii wewnętrznej cząstek układu. Nie uwzględnia się jednak energii kinetycznej układu
jako całości oraz energii potencjalnej oddziaływań składników układu z polami
zewnętrznymi. Energia wewnętrzna jest funkcją stanu, tzn. jej zmiana zależy tylko od
wartości w stanach końcowym i początkowym przemiany. Nie zależy od rodzaju przemiany
czyli od stanów pośrednich.
1
Energię wewnętrzną można zmienić w wyniku dwóch różnych procesów. Pierwszy
polega na wykonaniu pracy przez siły zewnętrzne i w ten sposób zmiany objętościowe dobrze
izolowanego układu za ich pośrednictwem mogą doprowadzić do zmiany energii
wewnętrznej. Taki sposób przekazu energii może być zrealizowany np. za pośrednictwem
tłoka poruszającego się wewnątrz izolowanego cieplnie cylindra z gazem. Tak więc praca sił
zewnętrznych za pośrednictwem uporządkowanego ruchu tłoka może zmienić energię
wewnętrzną cząsteczek gazu. Drugi proces polega na przekazie ciepła do układu. Przekaz ten
powoduje wzmożenie intensywności chaotycznego ruchu cząstek układu. Można go
zrealizować w wyżej wspomnianym cylindrze; np. przy stałej objętości cylindra usuwa się
izolację cieplną jego ścianek. Cząsteczki gazu w cylindrze zderzając się z gorącymi
( zimnymi ) ściankami uzyskują większą ( mniejszą ) energię.
Zasady termodynamiki
Zerowa zasada termodynamiki
Jeśli układy A i B mają tę samą wartość dowolnej funkcji stanu i podobnie jest w
układach A i C, to układy B i C mają tę samą wartość tej funkcji stanu.
Proste zastosowanie tej zasady to np. pomiar temperatury za pomocą sensora A.
Powiedzmy, że sensor A zmierzył temperaturę ciała B i wynosiła ona T. Jeśli następnie sensor
A wyznaczył temperaturę ciała C – także T, to na podstawie zerowej zasady termodynamiki
twierdzimy, że temperatura ciał B i C jest taka sama.
Pierwsza zasada termodynamiki
Ciepło Q pobrane przez układ jest zużywane na wzrost energii wewnętrznej układu
(U 2 − U1 )
i na wykonaną przez układ pracę W :
Q = U 2 − U1 + W .
(6.1)
2
Zasada ta wyraża prawo zachowania energii. Inne jej sformułowanie to: Nie jest możliwe
perpetuum mobile pierwszego rodzaju, tzn. nie można zbudować okresowo pracującego
silnika, który wykonywałby większą pracę niż pobierałby energii z zewnątrz.
Pierwszą zasadę można podać w postaci różniczkowej:
dQ = dU + dW .
(6.2)
Pracę elementarną dW wygodnie jest przedstawić w postaci:
A – przekrój tłoka, dx - przesunięcie tłoka, dV = Adx - zmiana objętości, p - ciśnienie gazu,
G G
dW = Fds = Fdx = pAdx = pdV ,
W=
(6.3)
V2
∫ pdV .
(6.4)
V1
dQ = dU + pdV
(6.5)
Ciepło, pracę i energię wewnętrzną mierzymy w dżulach. Ciepło i praca nie są funkcjami
stanu w odróżnieniu od energii wewnętrznej.
3
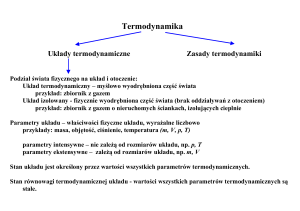
Druga zasada termodynamiki
O ile pierwsza zasada termodynamiki wyraża zasadę zachowania energii, to druga
zasada pozwala określić kierunkowość procesów termodynamicznych. Jedno ze sformułowań
tej zasady stanowi, że: Ciepło przepływa od ciała o wyższej temperaturze do ciała o niższej
temperaturze. Inne znane sformułowanie tej zasady brzmi: Niemożliwe jest perpetuum mobile
drugiego rodzaju, tzn. pracujący okresowo silnik, który pobierałby ciepło od jednego
zbiornika i zamieniałby to ciepło całkowicie na pracę.
Trzecia zasada termodynamiki – twierdzenie Nersta
Nie można za pomocą skończonej liczby kroków sprowadzić temperatury układu do
temperatury zera bezwzględnego.
Więcej na temat drugiej i trzeciej zasady termodynamiki powiemy na wykładzie z fizyki
statystycznej.
Gaz doskonały
Przez gaz doskonały rozumiemy zbiór cząstek o znikomo małych rozmiarach nie
oddziaływujących ze sobą poza momentami kiedy się zderzają. Gazy rzeczywiste posiadają
własności gazu doskonałego przy niskich ciśnieniach. Gaz doskonały stanowi najprostszy
modelowy układ termodynamiczny.
Empirycznie ustalono, że parametry termodynamiczne gazu doskonałego: ciśnienie p,
objętość V i temperatura bezwzględna T spełniają związek
pV
= const ,
T
(6.6)
o ile masa gazu w zbiorniku jest stała. Gazy doskonałe spełniają prawo Avogadra, które
stanowi, że w warunkach takiej samej temperatury i tego samego ciśnienia mol każdego gazu
4
zajmuje tę samą objętość. W tzw. warunkach normalnych: T = 273K ( t = 0D C ) ,
p = 1Atm = 1, 013 ⋅ 105 Pa ta objętość wynosi Vm = 22, 4l = 22, 4 ⋅ 10−3 m3 /mol. Na podstawie
tych danych można wyznaczyć stałą w równaniu (6.6):
pVm 1, 013 ⋅ 105 Pa⋅22, 4 ⋅10−3 m3 /mol
J
=
= 8, 31
= R,
T
273K
mol K
gdzie R = 8, 31 J/ ( mol K ) to uniwersalna stała gazowa. W ogólnym przypadku kiedy mamy
n moli gazu, równanie (6.6) można zapisać w postaci
pV = nRT =
m
μ
RT ,
(6.7)
gdzie m to masa gazu, μ - masa molowa. Równanie (6.7) nosi nazwę równania stanu gazu
doskonałego, lub równania Clapeyrona.
Przypomnimy pojęcia, które będą stosowane w dalszym toku wykładu:
•
1 mol – ilość substancji zawierająca taką samą liczbę cząstek ( atomów, cząsteczek,
jonów, elektronów ) co 0,012 kg izotopu 12C . W jednym molu liczba cząstek wynosi
N A = 6, 022 ⋅ 1023
•
1
i nosi nazwę – liczba Avogadra
mol
Masa molowa μ - masa jednego mola.
Równanie stanu można zapisać w różnych postaciach:
pV =
gdzie k =
mN A R
T = NkT ,
μ NA
(6.8)
R
J
= 1, 38 ⋅ 10 −23 to stała Boltzmanna, a N to ilość cząsteczek gazu w naczyniu,
NA
K
lub w postaci
p = nkT ,
5
gdzie n =
N
oznacza koncentrację ( ilość cząstek w jednostce objętości ) gazu, albo też
V
m pμ
pμ
=
⇒ρ =
,
V RT
RT
(6.9)
gdzie ρ oznacza gęstość gazu.
Ciepło molowe gazu doskonałego
Pojemność cieplna ciała K c
Kc ≡
dQ
,
dT
(6.10)
jest to ilość ciepła potrzebna do zmiany temperatury ciała o jednostkę. Powszechnie jednak
używa się innej miary do określenia zdolności danego ciała do przyjmowania czy też
oddawania ciepła – ciepła właściwego substancji c
c≡
dQ
,
mdT
(6.11)
gdzie m jest masą ciała. Ta definicja pozwala określić przyrost ciepła dQ wzorem dobrze
znanym z równań bilansu cieplnego
dQ = mcdT .
(6.12)
W przypadku kiedy jako miara ilości materii używany jest mol, wygodnie jest operować
pojęciem ciepła molowego, definiowanego jako ilość ciepła potrzebna do zmiany temperatury
1 mola ciała o 1 Kelwin
C≡
dQ
,
ndT
(6.13)
gdzie n to ilość moli. Ciepło molowe C łączy z ciepłem właściwym c relacja
6
C = cμ ,
(6.14)
gdzie μ to masa molowa.
Dla gazów wygodnie jest wprowadzić pojęcie ciepła molowego przy stałej objętości
CV i ciepła molowego przy stałym ciśnieniu C p .
⎛ dQ ⎞
CV ≡ ⎜
,
⎟
⎝ ndT ⎠V =const
a ponieważ z pierwszej zasady termodynamiki (6.5) wynika, że dla V = const
dQ = dU to CV =
(6.15)
dW = 0 i
dU
, i
ndT
dU = nCV dT .
(6.16)
Z wzoru (6.16) wynika, że dla stałego CV : U = nCV T + const i
ΔU = nCV ΔT ,
(6.17)
czyli dla gazu doskonałego zmiana energii wewnętrznej Δ U zależy od różnicy temperatur w
stanie końcowym i początkowym przemiany.
Ciepło molowe przy stałym ciśnieniu C p jest definiowane równaniem
⎛ dQ ⎞
.
Cp ≡ ⎜
⎟
⎝ ndT ⎠ p =const
(6.18)
Między C p i CV istnieje związek, który wynika z pierwszej zasady termodynamiki oraz z
równania Clapeyrona
dQ = dU + pdV / ( ndT ) ,
dQ
dU pdV
=
+
,
ndT ndT ndT
(6.19)
7
pV = nRT ,
przy stałym ciśnieniu otrzymamy pdV = nRdT i
dU nRdT
⎛ dQ ⎞
=
+
,
⎜
⎟
ndT
⎝ ndT ⎠ p =const ndT
a ponieważ
dU
= CV , otrzymamy
ndT
C p = CV + R.
(6.20)
Przemiany gazowe
1. Przemiana izotermiczna T = const.
Z równania stanu (6.7) otrzymamy
pV = const.
(6.21)
Pierwsza zasada termodynamiki pozwala obliczyć ciepło i pracę przemiany dQ = dW = pdV
Q =W =
∫
V2
V1
pdV =
∫
V2
V1
V2 dV
p1V1
dV = p1V1 ∫
= p1V1 ln V
V1 V
V
V2
V1
= p1V1 ln
V2
V
= nRT ln 2 . (6.22)
V1
V1
2. Przemiana izochoryczna V = const.
Z równania stanu otrzymamy
p
= const ,
T
(6.23)
Q = ΔU = nCV (T2 − T1 ), W = 0.
(6.24)
dQ = dU = nCV dT , dW = 0,
3. Przemiana izobaryczna p = const.
Z równania stanu
V
= const
T
(6.25)
8
W=
V2
∫ pdV = p (V
2
− V1 ) , ΔU = nCV ( T2 − T1 ) , Q = nC p ( T2 − T1 ) .
(6.26)
V1
4. Przemiana adiabatyczna dQ = 0.
Jest to przemiana bez wymiany ciepła z otoczeniem. Ma duże znaczenie przy omawianiu
modelowego cyklu zamkniętego – cyklu Carnota, a także przy objaśnianiu mechanizmu
rozchodzenia się fali dźwiękowej w gazach. Dla tej przemiany z definicji dQ = 0 . Z
pierwszej zasady termodynamiki otrzymamy 0 = dU + dW , czyli nCV dT + pdV = 0. Po
zróżniczkowaniu równania stanu mamy
pdV + Vdp = nRdT
i dalej
pdV + Vdp
+ pdV = 0,
nR
CV ( pdV + Vdp ) + RpdV = 0,
nCV
( CV + R ) pdV + CVVdp = 0,
C p pdV + CVVdp = 0 / ( pVCV )
po oznaczeniu
Cp
CV
= κ mamy
dV dp
+
= 0,
V
p
κ d ln(V ) + d ln( p ) = 0,
κ
d ( ln(V κ ) + ln( p ) ) = 0,
d ln ( pV κ ) = 0,
i ostatecznie
pV κ = const.
(6.27)
9
Równanie adiabaty (6.27) znane jest jako równanie Poissona. Korzystając z równania
Clapeyrona można je także przedstawić w postaci
TV κ −1 = const ,
(6.28)
p1−κ T κ = const.
(6.29)
lub
Wykładnik adiabaty κ =
Cp
CV
dla gazów jednoatomowych wynosi
5
, dla gazów
3
7
4
dwuatomowych κ = , a dla gazów wieloatomowych κ = . Równanie Poissona
5
3
pV κ = const jest podobne do równania izotermy pV = const , jednak z uwagi na to, że
wykładnik adiabaty κ > 1 adiabata jest bardziej stroma od izotermy.
Uzasadnienie podanych wartości κ zostanie przedstawione w części wykładu dotyczącej
fizyki statystycznej.
Z definicji przemiany adiabatycznej dQ = 0 , ciepło przemiany Q = 0 oraz
dW = −dU = − nCV dT , W = −ΔU = − nCV (T2 − T1 ) .
(6.30)
10
Wzór barometryczny
Otrzymamy teraz prawo, według którego zmienia się ciśnienie atmosferyczne w
zależności od wysokości.
Ciśnienie dp wywierane przez
pionowy słup powietrza o
przekroju A zawarty między
wysokościami h i h + dh można
obliczyć z
p − ( p + dp ) =
− dp = ρ gdh.
Z równania stanu (6.9): ρ =
zależności
dm g ρ Adhg
=
A
A pμ
otrzymamy
RT
dp = −
pμ
gdh ⇒
RT
dp μ g
+
dh = 0.
p RT
Dalej założymy, że powietrze oprócz tego, że jest gazem doskonałym, to jeszcze jego
temperatura nie zmienia się z wysokością, wtedy
μg ⎤
μg
⎡
d ⎢ln( p ) +
h ⎥ = 0 ⇒ ln( p ) +
h = const ,
RT ⎦
RT
⎣
i z warunku brzegowego: dla h = 0 ; p = p0 otrzymamy
ln( p0 ) +
μg
⎛ p⎞
μg
0 = const ⇒ ln ⎜ ⎟ = −
h,
RT
RT
⎝ p0 ⎠
i ostatecznie otrzymamy wzór barometryczny
p = p0 e
−
μ gh
RT
.
(6.31)
11