Historia liczby π

Historia liczby π
Historia π (czyt. Pi)
Już w czasach zamierzchłych starożytni rachmistrze
zauważyli, że wszystkie koła mają ze sobą coś
wspólnego, że ich średnica i obwód pozostają wobec
siebie w takim samym stosunku, a liczba ta bliska jest
3.
Kiedy liczba π została po raz pierwszy
użyta?
Symbol π został pierwszy raz użyty w 1706 roku
przez matematyka angielskiego Wiliama Jonesa. W
powszechne użycie wszedł dopiero w połowie XVIII
wieku po wydaniu Analizy L. Eulera. Najważniejszą
w historii liczby π, prawdziwie przełomową datą
był rok 1882, w którym matematyk niemiecki F.
Lindemann wykazał ostatecznie, że liczba π jest
liczbą przestępną (to znaczy, że nie może ona być
pierwiastkiem równania algebraicznego o
współczynnikach całkowitych). Wykazał on w ten
sposób nierozwiązalność słynnego w starożytności
zagadnienia kwadratury koła.
Pi – fascynująca liczba
Liczba π nazywana bywa często „ludolfiną”. Nazwa
„ludolfina” pochodzi od imienia matematyka
holenderskiego Ludolfa van Ceulena, który w 1610
roku obliczył wartość liczby π z dokładnością do 35
cyfr po przecinku. Interesująca jest historia tej liczby.
Liczba π przechodziła wiele przemian i odmian. Od
ustalonej przez Archimedesa wartości 22/7 , która
dawała dwa rzędy dziesiętne po przecinku, dochodzi
do rozwinięcia dziesiętnego z 707 cyframi po
przecinku, danego przez Shanksa.
Poniższa tabela wskazuje przebieg tego postępu, z
pominięciem jednak drobnych zmian od roku 250
przed naszą erą do roku 1464 naszej ery.
Dawne przybliżenia liczby π
Babilończycy (ok. 2000 r. p.n.e.):
π≈3
Egipcjanie (ok. 2000 r. p.n.e.):
π≈(16/9)²≈3,160493...
Archimedes (III w. p.n.e.):
π≈22/7≈3,14
Chiński matematyk Chang Hing (I w. n. e.):
π≈ 142/45≈3,1555...
Klaudiusz Ptolomeusz (II w. n.e.):
π≈3+8/60+3/360≈3,1416
hinduski matematyk Ariabhata (V w. n.e.):
π≈6283220000≈3,1416
hinduski matematyk Bhasakara (VII w. n.e.):
π≈754/240=3,1416666...
włoski matematyk Leonardo Fibonacci (XIII w.):
π≈864/275≈3,1415929
holenderski matematyk Piotr Metius (XVI w.):
π≈355/113≈3,1415929
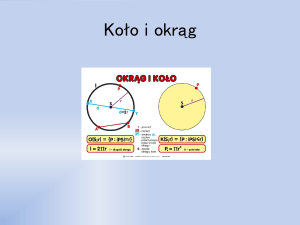
Wyznaczenie obwodu koła
• Obwód koła jest proporcjonalny do jego
średnicy. Współczynnikiem proporcjonalności
jest liczba π.
Zależność tą wyrażamy wzorem:
L=2* π *r
• r - promień koła
• π - współczynnik proporcjonalny, liczba pi,
która w przybliżeniu równa jest wartości 3,14
Ciekawostki na
temat liczby π
• Znak π jest oznaczeniem matematycznym
wywodzącym się z litery alfabetu greckiego
powszechnie używanym do oznaczenia liczby,
której wartością jest stosunek długości
obwodu koła do długości jego średnicy.
• Jej pierwszego utożsamienia z wartością
3,14159… dokonał to w 1706 William Jones,
walijski matematyk i pisarz.
• Z liczbą π, jakkolwiek pojawia się ona w wielu
wzorach z różnych dziedzin, ludzie zetknęli się już w
starożytności, zauważając, że stosunek obwodu
koła do jego średnicy jest wartością stałą.
Babilończycy przyjmowali, że jest on równy w
przybliżeniu 3.
• Pierwsze źródła świadczące o świadomym
korzystaniu z własności liczby π pochodzą ze
starożytnego Babilonu. Na jednej z kamiennych
tablic, pojawia się opis wartości obwodu koła o
średnicy 1, przybliżony przez wartość 3.125
• W piramidzie Cheopsa stosunek sumy dwóch
boków podstawy do wysokości wynosi 3,1416,
czyli przybliżenie pi z dokładnością do czterech
miejsc po przecinku! Dziś nie można stwierdzić
czy był to zadziwiający przypadek, czy wynik
geniuszu nieznanych nam z imienia uczonych.
• Uczeni szukając kontaktu z cywilizacjami
pozaziemskimi, wysłali w kosmos drogą radiową
informację o wartości liczby π. Wierzą, że
inteligentne istoty spoza Ziemi znają tę liczbę i
rozpoznają nasz komunikat.
• Zdaniem dr. Badowskiego, choć liczba Pi inspiruje
hobbystów, uczonych a nawet artystów, wcale
nie musi być tak wyjątkowa, jak może się
wydawać. Dowodem na to może być aplikacja,
która w rozwinięciu dziesiętnym liczby Pi poszuka
naszej daty urodzenia. Jest dowód naukowy na
to, że w tym rozwinięciu znajdzie się ciąg
liczbowy dowolnej długości. To pokazuje, że nie
jest liczbą szczególną. Nie ma żadnego porządku
w jej rozwinięciu dziesiętnym. Nie jest w
jakikolwiek sposób wybrana - podkreślił
Badowski.
• Do opisania koła wpisanego we wnętrze naszej
planety wystarczy liczba π przybliżona do 11 cyfr
po przecinku. Obliczenia takie obarczone byłyby
błędem do 1 mm. Do opisania koła wpisanego w
cały dostrzegalny kosmos wystarczy liczba
π podana z dokładnością do 39 miejsc po
przecinku, przy czym wartość błędu byłaby
porównywalna do promienia atomu wodoru.
• Liczba π ma swoich licznych wielbicieli.
Obchodzą oni dzień π (14 marca) (amerykański
sposób zapisu daty 3.14).Tworzone są też
wierszyki i opowiadania, w których długość
każdego kolejnego słowa jest równa kolejnej
cyfrze w rozwinięciu dziesiętnym liczby π.
• Niemcom w zapamiętaniu aproksymacji π
uzyskanej przez van Ceulena może być
pomocny wiersz napisany przez Clemensa
Brentano, który jest przypuszczalnie
pierwszym tego typu tekstem:,,Nigdy, o dobry
Boże, nie użyczysz mi mocy spamiętania po
wsze czasy potężnego, ze sobą trwale
sprzężonego szeregu cyfr. Dlatego przyswoiłem
sobie ludolfinę w słowach.’’
• Światowy potwierdzony rekord w zapamiętywaniu
ciągu cyfr liczby π należy aktualnie do Japończyka
Akiry Haraguchi, który podał ją z dokładnością do
100 tysięcy miejsc po przecinku bijąc własny
rekord 83 431 cyfr po przecinku z roku 1995.
Starszy rekord należał do Chińczyka Lu Chao, który
powtórzył ponad 67 tysięcy znaków po przecinku.
Żródło
• pl.wikipedia.org/wiki/Pi‎
• www.math.edu.pl › ciekawostki › liczby‎
• www.rmf24.pl/ciekawostki/news-poznajcie-ludolfine-czylinajslynniejsza...‎
• www.wykop.pl/link/508727/‎
• e-kursant.com.pl/aciekawostki/334-10-najciekawszychinformacji-o-licz...‎
KONIEC