Koło i okrąg
Liczba jest liczbą niewymierną,
określającą stosunek długości
okręgu do długości jego średnicy.
Niezwykła Liczba…
Liczba pi od dawna fascynuje ludzi…
Symbol π wprowadził w 1706 roku William Jonw
książce Synopsis Palmariorum Mathesos (π
jest pierwszą literą greckiego słowa
περίμετρον - perimetron, czyli obwód) a
rozpowszechnił go później Leonhard Euler.
Lambert udowodnił, że π nie jest pierwiastkiem
kwadratowym żadnego ułamka.
Liczba
• Liczba Pi nazywana bywa często „ludolfiną”.
Nazwa „ludolfina” pochodzi od imienia
matematyka holenderskiego Ludolfa van Ceulena,
który w 1610 roku obliczył wartość liczby Pi z
dokładnością do 35 cyfr po przecinku. Zapis ten
wyryto nawet na jego nagrobku.
3,14159265358979323846264338327950288…
O liczbie
• „Następnie sporządził odlew okrągłego morza
o średnicy dziesięciu łokci, o wysokości 5 łokci i
o obwodzie 30 łokci.”- Biblia Tysiąclecia
Wzory na π
Oto wzory na liczbę pi, jakie pojawiały się w pracach uczonych tego świata.
Babilończycy (ok. 2000 r. p.n.e.): π≈3
Egipcjanie (ok. 2000 r. p.n.e.): π≈(169)2≈3,160493...
Archimedes (III w. p.n.e.): π≈ 22 7 ≈ 3,14
Chiński matematyk Chang Hing (I w. n. e.): 14245≈3,1555...
Klaudiusz Ptolomeusz (II w. n.e.): π≈3+860+3360≈3,1416
hinduski matematyk Ariabhata (V w. n.e.): π≈6283220000=3,1416
hinduski matematyk Brahmagupta (VII w. n.e.): π≈10≈3,162...
hinduski matematyk Bhasakara (VII w. n.e.): π≈754240=3,1416666...
włoski matematyk Leonardo Fibonacci (XIII w.): π≈864275≈3,1415929
holenderski matematyk Piotr Metius (XVI w.): π≈355113≈3,1415929
francuski matematyk Francois Viete (XVI w.): π2=22·2+22·2+2+22·...
angielski matematyk John Wallis (XVII w.): π2=2·2·4·4·6·6·...3·3·5·5·7·7·...
niemiecki matematyk Gottfried Wilhelm Leibniz (XVII w.): π4=1-13+15-17+19+...
szwajcarski matematyk Leonhard Euler (XVIII w.): π26=1+122+132+142+152+...
Kwadratura koła
Kwadratura koła – problem polegający na
skonstruowaniu kwadratu, którego pole równe
jest polu danego koła przy użyciu wyłącznie cyrkla
i linijki bez podziałki. Jest to jeden z trzech
wielkich problemów starożytnej matematyki
greckiej (obok trysekcji kąta i podwojenia
sześcianu), sformułowany przez szkołę
pitagorejską.
Określenie kwadratura koła funkcjonuje również w
języku potocznym; oznacza coś niewykonalnego, z
góry skazanego na niepowodzenie.
Ciekawostki
•
•
•
•
W piramidzie Cheopsa stosunek sumy dwóch boków podstawy do wysokości
wynosi 3,1416, czyli przybliżenie pi z dokładnością do czterech miejsc po
przecinku! Dziś nie można stwierdzić czy był to zadziwiający przypadek, czy wynik
geniuszu nieznanych nam z imienia uczonych.
Uczeni szukając kontaktu z cywilizacjami pozaziemskimi, wysłali w kosmos drogą
radiową informację o wartości liczby π. Wierzą, że inteligentne istoty spoza Ziemi
znają tę liczbę i rozpoznają nasz komunikat.
31 grudnia 2009 roku francuski informatyk Fabrice Bellard obliczył matematyczną
stałą pi z dokładnością do prawie 2,7 biliona miejsc po przecinku. To wynik
dokładniejszy od poprzedniego rekordu o blisko 123 miliardy cyfr.
Sześćdziesięcioletni Akira Haraguchi wyrecytował z pamięci 100 tys. miejsc po
przecinku liczby pi. Zajęło mu to 16 godzin. Pobił w ten sposób własny rekord z
1995 roku. Wtedy jednak doszedł "tylko" do 83431. miejsca po przecinku.
Wydarzenie miało miejsce w Kisarazu na wschodzie Tokio. Podczas bicia rekordu
Haraguchi robił sobie co dwie godziny pięciominutowe przerwy na odpoczynek i
małą przekąskę w postaci kulek z ryżu. W Księdze rekordów Guinnessa nie widnieje
nazwisko Haraguchiego. Oficjalnie rekord należy do innego Japończyka, Hiroyuki
Goto, który również w 1995 roku wyrecytował 42195 miejsc po przecinku słynnej
liczby pi.
Święto liczby Pi
Liczba Pi jest na tyle wyjątkowa, że ma ... swoje święto!
14 marca obchodzimy Międzynarodowy Dzień Pi.
Data jest nieprzypadkowa, ponieważ według
amerykańskiego zapisu daty 14 marca to 3.14, czyli
zaokrąglenie liczby Pi do dwóch miejsc po przecinku.
Wielbiciele liczby Pi, zwłaszcza dotyczy to amerykańskich
naukowców, w dniu święta zajadają się specjalnymi
okrągłymi ciastami, które wewnątrz udekorowane jest
literą Pi, a na obwodzie podane ma jej rozwinięcie
dziesiętne.
Pi, pi, pi
Koło
• Koło – zbiór wszystkich punktów płaszczyzny,
których odległość od ustalonego punktu na tej
płaszczyźnie (środka koła) nie przekracza
pewnej wartości (promienia koła).
• Równoważna definicja: część płaszczyzny
ograniczona przez pewien okrąg; okrąg ten
zawiera się w kole i jest zarazem jego
brzegiem.
Okrąg
• Okrąg – brzeg koła; zbiór wszystkich punktów
płaszczyzny euklidesowej odległych od
ustalonego punktu, nazywanego środkiem, o
zadaną odległość, nazywaną promieniem.
Średnica okręgu ,łuk okręgu, cięciwa
okręgu
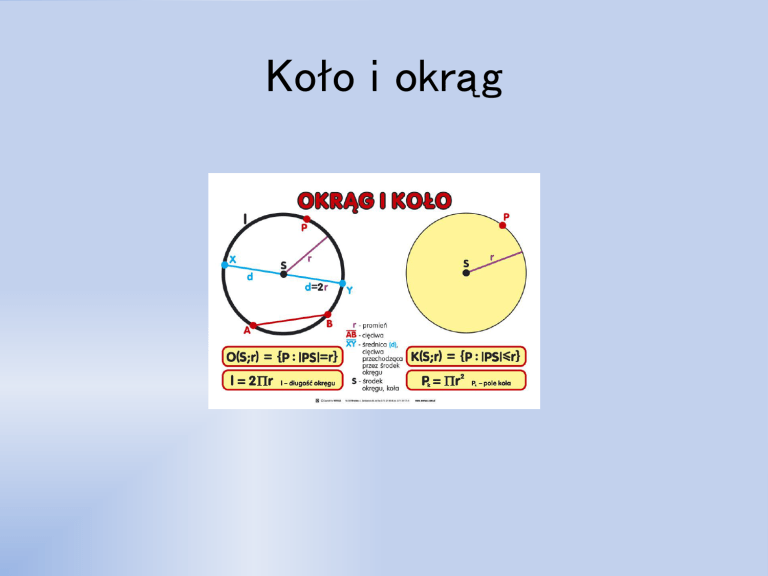
Odcinek, który łączy dowolny punkt okręgu ze środkiem okręgu (koła), to promień okręgu (koła).
Okrąg o środku S i promieniu długości r oznaczamy o(S, r).
Koło o środku S i promieniu długości r oznaczamy k(S, r).
Łuk okręgu to jedna z dwóch części okręgu wyznaczona przez dwa punkty tego okręgu (AB).
Cięciwa okręgu (koła) to odcinek łączący dwa różne punkty okręgu (CD).
Średnica okręgu (koła) - to najdłuższa z jego cięciw, która przechodzi przez środek okręgu (koła) (EF).
Pole koła (P) i długość okręgu (L):
P = πr2
L = 2πr
gdzie π (pi) to stosunek długości okręgu do długości jego średnicy, który jest wielkością stałą i wynosi w
przybliżeniu 3,1415..., a r to długość promienia koła.
Sieczna to prosta mająca z okręgiem dokładnie dwa punkty wspólne, prostą mająca dokładnie jeden punkt
wspólny nazywamy styczną do okręgu.
Okrąg i koło
Koło znane było we wszystkich kulturach od
najdawniejszych czasów. Zastosowane zostało
tam, gdzie zachodziła potrzeba transportu na
większe odległości. Wykorzystanie koła jako koło
jezdne pojawiło się ok. 3500 lat p.n.e. w
Mezopotamii. Trudno sobie wyobrazić świat bez
koła, tę figurę rozpoznaje każdy. Z pojęciem koła
wiąże się pojęcie okręgu, które można określić
jako krzywą, którą zakreśla koniec odcinka,
obracającego się dokoła pewnego danego
punktu.
Wykorzystanie koła i okręgu
w życiu codziennym
•
•
•
•
•
•
Motoryzacja
Mechanika
Rozrywka
Ratownictwo
Tkactwo
I Inne…
Zadanie
• Oblicz obwód koła
a) o promieniu r = 1 cm.
b) o średnicy d = 6 cm.
c) o średnicy równej przekątnej kwadratu o boku 1 cm.
W wyniku pozostaw liczbę π.
Rozwiązanie:
Obwód = 2πr i też obwód = πd, gdzie r jest promieniem, a d średnicą.
a) Obwód = 2·πr = 2·π·1 cm = 2π cm,
b) Obwód = πd = π·6 cm = 6π cm.
c) Długość przekątnej kwadratu wyraża się wzorem , gdzie a jest bokiem
kwadratu, więc cm, zatem obwód równa się cm.
Miasto Koło
• Miasto zostało lokowane w 1362 na wyspie rzecznej przez
Kazimierza Wielkiego. Położone w dogodnym miejscu, nie
posiadało murów obronnych. Od XV wieku do 1716 r.
odbywały się tutaj sejmiki szlachty prowincji wielkopolskiej.
W 1655 r. zostało zniszczone przez wojska szwedzkie. W
1793 r. miasto znalazło się pod zaborem pruskim, a od 1815
r. w Królestwie Kongresowym. W 1842 r. założono tutaj
pierwszą fabrykę fajansu. Podczas okupacji niemieckiej
zginęło ponad trzy tysiące mieszkańców miasta. Miasto
zostało odbite z rąk niemieckich przez Armię Czerwoną 20
stycznia 1945 r. Okres największego rozwoju miasta
przypadł na lata 60. i 70. XX wieku. Obecnie Koło jest
siedzibą powiatu w województwie wielkopolskim.












