uploads/Liczby rzeczywiste
advertisement
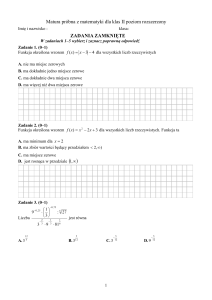
Liczby rzeczywiste – zadania kodowane 1. Każdą z czterech liczb występujących w wyrażeniu 1,275∙2,303 0,3985∙4,004 przybliżono z dokładnością do drugiego miejsca po przecinku i obliczono wartość takiego wyrażenia. Oblicz błąd względny otrzymanego w ten sposób wyniku z dokładnością do piątego miejsca po przecinku. Zakoduj trzy ostatnie cyfry wyznaczonej liczby. 2. Kwotę 6000zł wpłacono na trzyletnią lokatę oprocentowaną w wysokości 3,6% w skali roku z półroczną kapitalizacją odsetek. Oblicz zysk z tej lokaty. Nie uwzględniaj podatku od odsetek. Zakoduj część całkowitą obliczonego zysku. 3. Liczbę 60√8+√6 √8+√6 zapisano w postaci m+n√3 gdzie m i n są liczbami całkowitymi. Zakoduj cyfry: setek, dziesiątek i jedności. 4. Dane są liczby: k= 34∙5∙7∙116, l=26∙3∙5∙136, m= 22∙54∙14 i n= 2∙73∙113∙44. Liczby: 𝑎 a=NWD(k,l), b=NWD(m,n). Oblicz 𝑏 . Zakoduj trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku. 5. Cenę pewnego artykułu najpierw dwukrotnie obniżono, za każdym razem o 40%, a następnie dwukrotnie podniesiono, za każdym razem o 40%. Chcąc sprzedawać ten artykuł po wyjściowej cenie należałoby obecnie podnieść jego cenę o p%. Zakoduj cyfrę dziesiątek, cyfrę jedności i pierwszą cyfrę po przecinku rozwinięcia dziesiętnego liczby p. 6. Liczba n jest najmniejszą liczbą całkowitą spełniającą równanie: 2|x+57|=|x-39| Zakoduj cyfry: setek, dziesiątek i jedności liczby |n|. 7. Liczba a jest iloczynem wszystkich liczb spełniających równanie 1 | |𝑥 + 1| − 4| = 3 2 Zakoduj cyfry: setek, dziesiątek i jedności liczby a.
