Pole magnetyczne wytwarzane przez uzwojenia w szczelinie

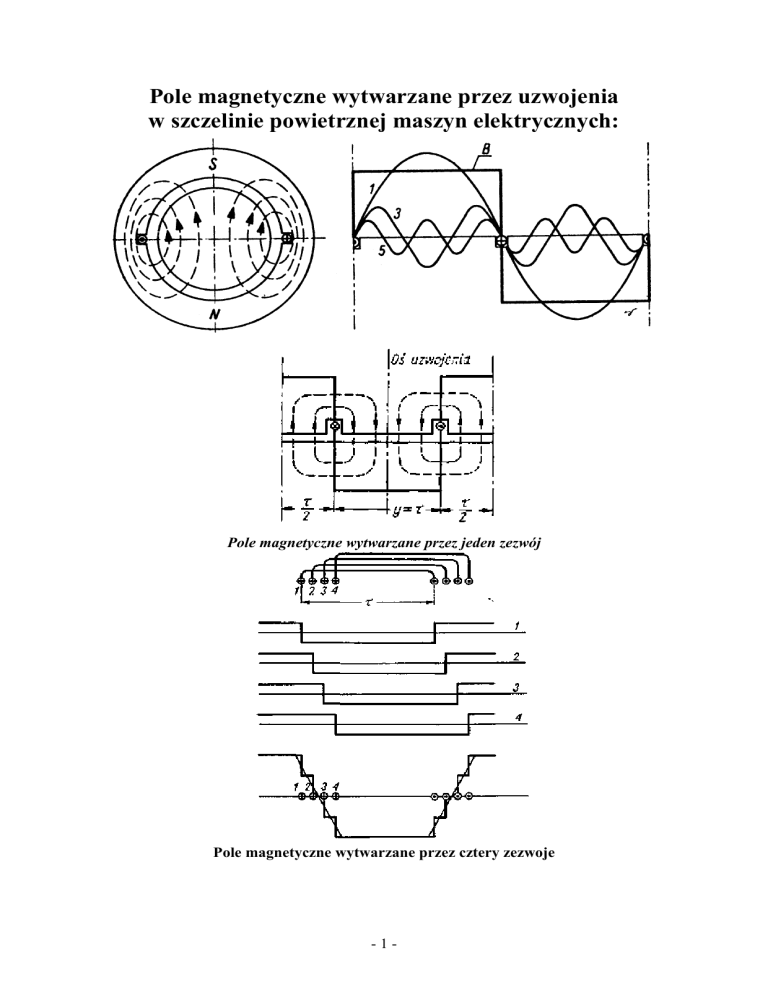
Pole magnetyczne wytwarzane przez uzwojenia
w szczelinie powietrznej maszyn elektrycznych:
Pole magnetyczne wytwarzane przez jeden zezwój
Pole magnetyczne wytwarzane przez cztery zezwoje
-1-
B1 =
∑
ν
1
=1, 3, 5,...
ν
Bm sin(να )
Połączenie szeregowo q zezwojów o rozpiętości y/τ powoduje, że wypadkowy
kształt będzie przebiegiem schodkowym opisanym zależnością:
B1 =
∑
ν
=1, 3, 5,...
sinνq
kqν
1
ν
k q k y Bm sin(να )
πp
π y
k qν = sinν
2τ
Ż
=
πp
q sinν
Ż
gdzie:
kq – współczynnik grupy
ky – współczynnik skrótu
y/τ - skrót zezwoju
Ż – liczba żłobków
q- liczba żłobków na biegun i fazę
Ż
q=
2 pm
Dzięki tym zabiegom otrzymujemy przebieg pola magnetycznego wytworzony przez
jedno uzwojenie rozłożone bliski sinusoidzie
Założenia:
1. równomierna szczelina powietrzna (brak żłobkowania, centryczne osadzenie
wirnika względem stojana)
2. rdzeń o przenikalności µr→∞ (pomijamy spadek napięcia magnetycznego w
rdzeniu – o właściwościach maszyny decydują zjawiska w szczelinie powietrznej;
pomijamy nasycenie obwodu magnetycznego) (liniowość obwodu magnetycznego)
3. uzwojenia wytwarzają pole magnetyczne o rozkładzie sinusoidalnym (pomijamy
„wyższe” harmoniczne pola magnetycznego) (założenie dopuszczalne dla
dwuwarstwowych uzwojeń skróconych rozłożonych równomiernie na obwodzie
maszyny)
-2-
Dla uproszczenia analizy przyjmijmy, że każde z uzwojeń ma taką samą liczbę zwojów i
przez każde z analizowanych uzwojeń płynie taki sam prąd, a zatem każde z uzwojeń
wytwarza taki sam przepływ.
Pole magnetyczne wytworzone przez pojedyncze uzwojenie można wyrazić zależnością:
b(α , t ) = Bm cos pα
Bm = C sin(ωt )
b(α , t ) = C sin ωt cos pα
Przyjmując, że stała C=1 otrzymamy:
b(α , t ) = sin ωt cos pα
1
b(α , t ) = [sin(ωt + pα ) + sin(ωt − pα )]
2
Wniosek 1):
Pojedyncze uzwojenie wytwarza pole pulsujące, które można traktować jak dwa
pola kołowe wirujące w przeciwnych kierunkach z prędkością wyznaczoną przez
warunek:
ωt − pα = const
Prędkość wirowania pola:
dα ω
Ω=
=
dt
p
Przyjmijmy, że mamy dwa identyczne uzwojenia, przy czym w przestrzeni są one
przesunięte o kąt ϕ’, natomiast prądy są przesunięte o kąt ϕ (przy jednakowej
amplitudzie). Pole magnetyczne wypadkowe składa się z sumy składników:
-3-
b1 (α , t ) = sin ωt cos pα
b2 (α , t ) = sin(ωt + ϕ ) cos( pα + ϕ )
'
b(α , t ) = sin ωt cos pα
+ sin(ωt + ϕ ) cos( pα + ϕ )
'
Rozkładając poszczególne składniki na pola wirujące zgodnie i przeciwnie otrzymamy:
1
b(α , t ) = {sin(ωt + pα ) +
2
+ sin(ωt − pα ) +
+ sin(ωt + pα + ϕ + ϕ ' ) +
+ sin(ωt − pα + ϕ − ϕ ' )}
Po zsumowaniu składników pola wirujących w tym samym kierunku przy
wykorzystaniu zależności:
sin α + sin β = 2 sin
α+β
2
cos
α−β
2
otrzymamy:
b(α , t ) =
sin(ωt + pα +
ϕ +ϕ'
+ sin(ωt − pα +
2
) cos
ϕ −ϕ'
2
-4-
ϕ +ϕ'
) cos
2
+
ϕ −ϕ'
2
Przypadek 1) ϕ=ϕ’=0 – otrzymujemy pole pulsujące
Przypadek 2) ϕ=0 i ϕ’≠0 – otrzymujemy pole pulsujące
Przypadek 3) ϕ≠0 i ϕ’=0 – otrzymujemy pole pulsujące
Przypadek 4) ϕ≠0 i ϕ’ ≠0 – otrzymujemy pole wirujące eliptyczne
Przypadek 4) ϕ+ϕ’ =180° i ϕ-ϕ’ =0 lub ϕ-ϕ’ =180° i ϕ+ϕ’ =0 – otrzymujemy pole
wirujące kołowe
Warunki powstawania pola wirującego
(eliptycznego lub kołowego):
-
co najmniej dwa uzwojenia przesunięte względem siebie o pewien kąt
(mechaniczny) na obwodzie maszyny
-
prądy płynące w tych uzwojeniach muszą być przesunięte w fazie o pewien kąt
(elektryczny)
Dla uzwojenia trójfazowego:
b(α , t ) = sin ωt cos pα +
+ sin(ωt + 120o ) cos( pα + 120o )
+ sin(ωt − 120o ) cos( pα − 120o )
Po zastosowaniu zależności:
sin ωt cos pα =
1
[sin(ωt + pα ) + sin(ωt − pα )]
2
otrzymamy:
1
b(α , t ) = {sin(ωt + pα ) + sin(ωt − pα ) +
2
+ sin(ωt + pα + 120o ) + sin(ωt − pα ) +
+ sin(ωt + pα − 120o ) + sin(ωt − pα )}
-5-
Oraz:
3
b(α , t ) = sin(ωt − pα )
2
Wniosek:
uzwojenie 3-fazowe symetryczne, przy symetrycznym zasilaniu wytwarza pole wirujące
kołowe!
-6-