Statystyka matematyczna

Pojęcie zmiennej losowej.
Przedmiotem statystyki matematycznej jest pewien sposób wnioskowania, w którym
przesłanki są prawdopodobne ( obarczone niepewnością ). Stąd na drodze dedukcji
wykorzystującej rachunek prawdopodobieństwa uzyskujemy wnioski, których
prawdopodobieństwo jest nie większe niż przesłanek. Przedmiotem badań statystyki
matematycznej jest relacja między częścią a całością, czyli populacją i próbą.
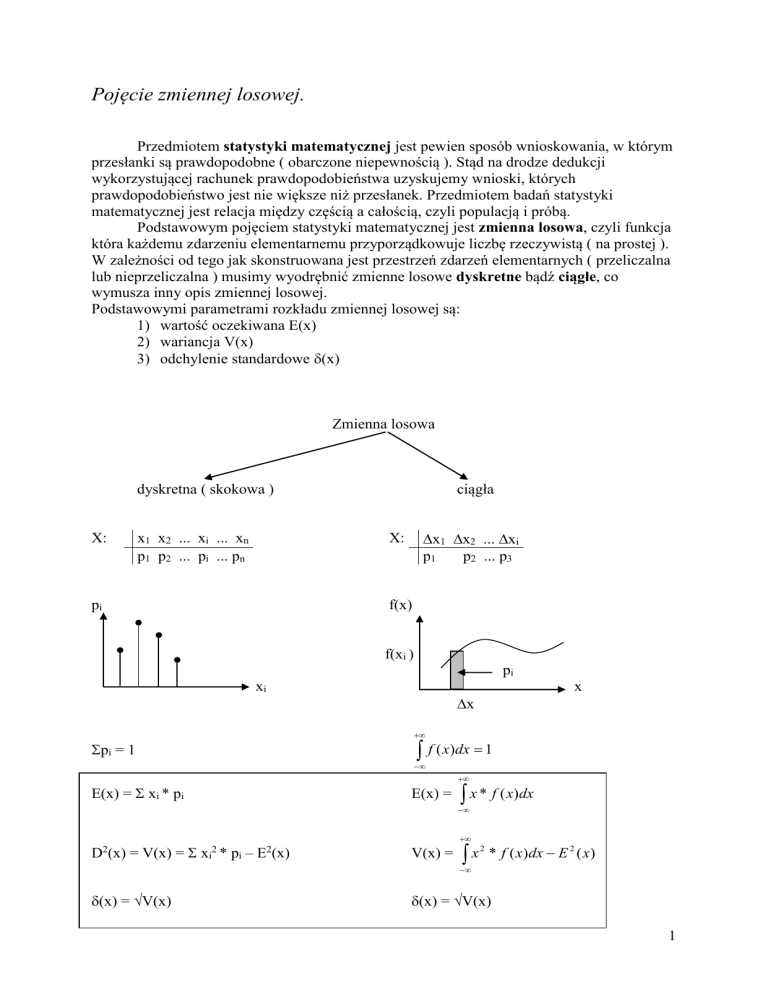
Podstawowym pojęciem statystyki matematycznej jest zmienna losowa, czyli funkcja
która każdemu zdarzeniu elementarnemu przyporządkowuje liczbę rzeczywistą ( na prostej ).
W zależności od tego jak skonstruowana jest przestrzeń zdarzeń elementarnych ( przeliczalna
lub nieprzeliczalna ) musimy wyodrębnić zmienne losowe dyskretne bądź ciągłe, co
wymusza inny opis zmiennej losowej.
Podstawowymi parametrami rozkładu zmiennej losowej są:
1) wartość oczekiwana E(x)
2) wariancja V(x)
3) odchylenie standardowe (x)
Zmienna losowa
ciągła
dyskretna ( skokowa )
X:
x1 x2 ... xi ... xn
p1 p2 ... pi ... pn
x1 x2 ... xi
p1
p2 ... p3
X:
pi
f(x)
f(xi )
pi
xi
x
x

pi = 1
 f ( x)dx  1


E(x) =  xi * pi
E(x) =
 x * f ( x)dx


D2(x) = V(x) =  xi2 * pi – E2(x)
V(x) =
x
2
* f ( x)dx  E 2 ( x)

(x) = V(x)
(x) = V(x)
1
Ex. 1.
Możemy przyjąć, że w obrocie papierami wartościowymi zmienną losową jest stopa
zysku, a ryzyko inwestowania może być mierzone wariancją zmiennej losowej. Biorąc pod
uwagę różne warianty stanu gospodarki przedstawiono następujący rozkład tej zmiennej
losowej:
Stan gospodarki
Szybki rozwój
Umiarkowany rozwój
Stagnacja
Niewielka recesja
Duża recesja
pi xi [%]
0,1 20
0,2
5
0,3
1
0,2 -1
0,2 -10
xi2
400
25
1
1
100
E(x) =  xi * pi = 20 * 0,1 + 5 * 0,2 + 1 * 0,3 + (-1) * 0,2 + (-10) * 0,2 = 1,1
V(x) =  xi2 * pi – E2(x) = 40*0,1 + 25*0,2 + 1*0,3 + 1*0,2 + 100*0,2 = 65,5 – 1,21 = 64,29
(x) = V(x) = 64,29 = 8,02
Wartość oczekiwana zysku wynosi ok. 1%, zaś ryzyko inwestora, czyli przeciętne odchylenie
wynosi  8%.
Ex.2.
Podaj wartość oczekiwaną i wariancję następującej funkcji gęstości
prawdopodobieństwa:
0
f(x) = cx
0
;x<0
;0x3
;x>3



 c * xdx  1
f ( x)dx  1


2
c *[

0
9 0
c*(  ) 1
2 2
x 3
]0  1
2
3
3
c *  xdx  1
c=
2
9
3
2 x3
2 27
2
2
E(x) =  x * f ( x)dx =  x * xdx = *  x 2 dx = * [ ]30  *
2
9
3
9 3
9
9 0

0
3
3
2 x4
2 81
2
2
V(x) =  x * xdx  2 2 = *  x 3 dx  4 = * [ ]30  4  *  4  0,5
9
4
9 4
9
9 0
0
2
(x) = V(x) = 0,5 = 0,71
2
Spis treści
Pojęcie zmiennej losowej. .......................................................................................................... 1
Dystrybuanta i jej własności. ................................................... Error! Bookmark not defined.
Nierówność Markowa i Czebyszewa. ...................................... Error! Bookmark not defined.
Własności parametrów rozkładu zmiennej losowej. ................ Error! Bookmark not defined.
Rozkład normalny ( Gaussa ) i jego własności. ....................... Error! Bookmark not defined.
Rozkłady statystycznie związane z rozkładem normalnym. .... Error! Bookmark not defined.
Twierdzenie graniczne Lindberga – Levy’ego. ........................ Error! Bookmark not defined.
Związek między próbą a populacją – wprowadzenie do wnioskowania statystycznego
(operator losowania, losowanie ze zwracaniem i bez zwracania). .......... Error! Bookmark not
defined.
Estymacja przedziałowa średniej i wariancji badanej populacji. ............ Error! Bookmark not
defined.
Weryfikacja hipotez statystycznych. ........................................ Error! Bookmark not defined.
Testy różnicy średnich w próbach zależnych i niezależnych. .. Error! Bookmark not defined.
Alfabetyczny spis haseł ........................................................... Error! Bookmark not defined.
3