Funkcja liniowa. Przekształcenia wykresu funkcji. Zad 1. Funkcja

Funkcja liniowa. Przekształcenia wykresu funkcji.


Zad 1. Funkcja liniowa opisana wzorem f  x   2  10 x  2 jest funkcją:
A. malejącą
B. rosnącą
C. stałą
D. niemalejącą
Zad 2. Do wykresu funkcji f  x   5 x  b należy punkt A0,9  , zatem:
A. b  0
B. b  9
C. b  9
D. b  5
Zad 3. Który z wykresów podanych funkcji liniowej przechodzi przez początek układu
współrzędnych?
A. y  2 x
B. y  2 x  6
C. y  5  x
D. y  3
Zad 4. Która z podanych liczb jest miejscem zerowym funkcji y  5 x  8
8
3
3
A.
B. 0
C.  1
D. 2
5
5
5
Zad 5. Ile jest równa wartość funkcji y  2 x  5 dla x  1
A. 3
B. – 3
C. 7
Zad 6
D. – 7
Zad 7
Zad 8
Funkcja f  x    m  2 x  5m  1 jest malejąca dla:
A. m   ,2   2, 
B. m  2, 
C. m   2,2
D. m  R
Zad 9
Wykres funkcji f  x   3 x  6 przecina oś OY w punkcie:
A. (-2,0)
B. (0,6)
C. (2,0)
D. (0,9)
Zad 10
Proste będące wykresami funkcji f  x   3x  4; g  x   3x  1 :
A. nie mają punktów wspólnych
B. mają jeden punkt wspólny (-4,1)
C. mają jeden punkt wspólny (4,-1)
D. mają nieskończenie wiele punktów wspólnych
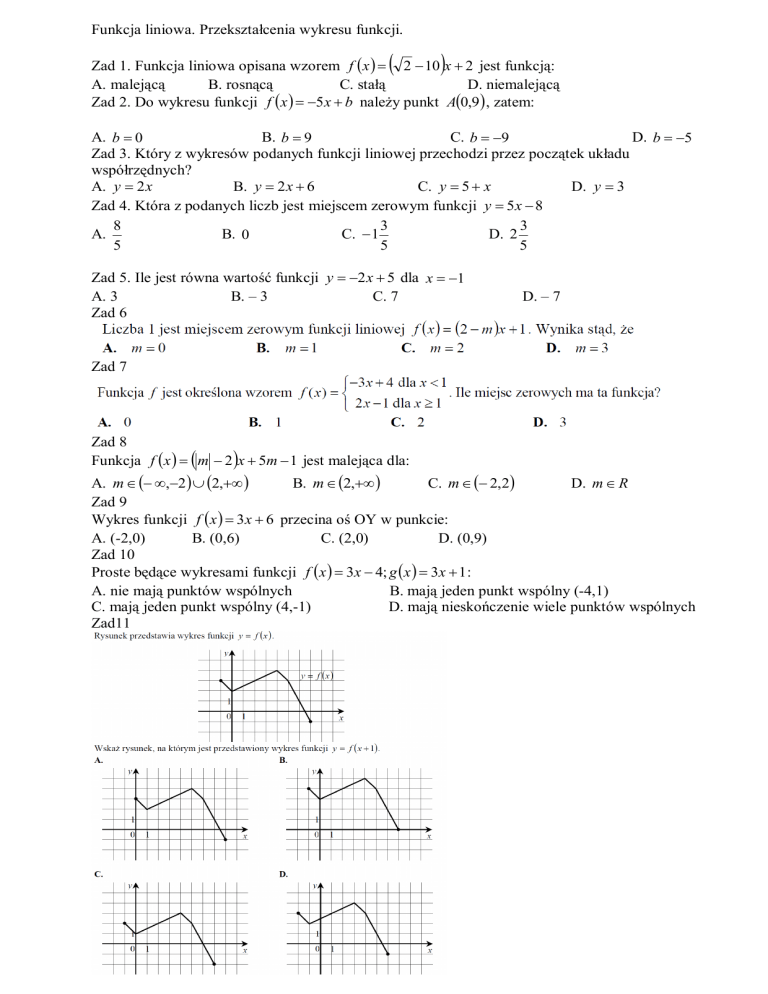
Zad11
Zad 12
Na rysunku jest przedstawiony fragment wykresu funkcji f, której dziedziną jest zbiór
–6, 6. Wykres funkcji f jest symetryczny względem osi OY.
a) Uzupełnij brakujący fragment wykresu
funkcji f.
b) Naszkicuj wykres funkcji g, opisanej
wzorem g(x) = f(x – 3) + 1.
c) Odczytaj z wykresu funkcji g zbiór
rozwiązań nierówności g(x) < 0.
d) Podaj maksymalne przedziały, w których
funkcja g jest malejąca.
e) Oblicz wartość wyrażenia
g(8)  g(  5 ) – g(1).
Zad 13 Na rysunku jest przedstawiony wykres funkcji f.
a) Naszkicuj wykres funkcji g(x) = f(–x).
b) Podaj zbiór rozwiązań równania g(x) = 2.
c) Podaj maksymalne przedziały, w których funkcja g
jest rosnąca.
Zad 14
Zad 15
Zad 16
Zad 17
Wyznacz wszystkie wartości parametru m, dla których funkcja f  x    m  2  7 x  2 jest stała.
Zad 18
Funkcja liniowa osiąga wartości dodatnie tylko dla x  3,  , a do jej wykresu należy punkt
A 1,8 . Wyznacz wzór tej funkcji.
Opracował: Waldemar Bałoń