GRAWITACJA

Powtórz i sprawdź swoje wiadomości z „grawitacji” – materiały
pomocnicze dla uczniów szkół ponadgimnazjalnych.
Materiał może być wykorzystany przez nauczycieli fizyki w postaci
foliogramu na lekcji powtórzeniowej.
Opracowali Cezary Misztela
Marek Pleszczyński
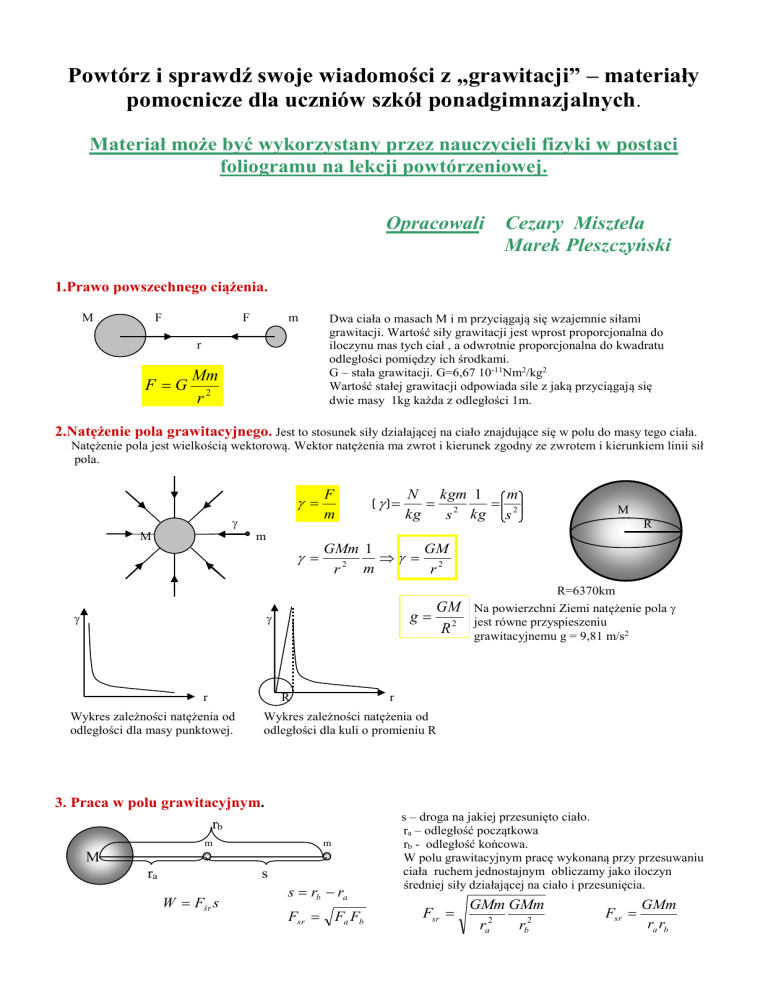
1.Prawo powszechnego ciążenia.
M
F
F
m
r
F G
Mm
r2
Dwa ciała o masach M i m przyciągają się wzajemnie siłami
grawitacji. Wartość siły grawitacji jest wprost proporcjonalna do
iloczynu mas tych ciał , a odwrotnie proporcjonalna do kwadratu
odległości pomiędzy ich środkami.
G – stała grawitacji. G=6,67 10-11Nm2/kg2
Wartość stałej grawitacji odpowiada sile z jaką przyciągają się
dwie masy 1kg każda z odległości 1m.
2.Natężenie pola grawitacyjnego. Jest to stosunek siły działającej na ciało znajdujące się w polu do masy tego ciała.
Natężenie pola jest wielkością wektorową. Wektor natężenia ma zwrot i kierunek zgodny ze zwrotem i kierunkiem linii sił
pola.
 

M
F
m
 
N kgm 1
m
 2
 2
kg
s kg s
m
M
R
M
 
GMm 1
GM
  2
2
m
r
r
MM
R=6370km

g

r
R
Wykres zależności natężenia od
odległości dla masy punktowej.
GM
R2
Na powierzchni Ziemi natężenie pola 
jest równe przyspieszeniu
grawitacyjnemu g = 9,81 m/s2
r
Wykres zależności natężenia od
odległości dla kuli o promieniu R
3. Praca w polu grawitacyjnym.
rb
m
m
M
ra
s
W  Fśr s
s  rb  ra
Fsr  Fa Fb
s – droga na jakiej przesunięto ciało.
ra – odległość początkowa
rb - odległość końcowa.
W polu grawitacyjnym pracę wykonaną przy przesuwaniu
ciała ruchem jednostajnym obliczamy jako iloczyn
średniej siły działającej na ciało i przesunięcia.
Fsr 
GMm GMm
ra2
rb2
Fsr 
GMm
ra rb
W
 r
r
GMm 
rb  ra  W  GMm b  a
 ra rb ra rb
ra rb 


1 1

  W  GMm  
r r
b 

 a
Praca wykonana przez siłę
zewnętrzną
1
m
M
2
1 1
W  GMm  
 ra rb 
W1=W2=W3
Praca wykonana przez siły pola
3
W polu grawitacyjnym praca zależy tylko od położenia początkowego i
końcowego , natomiast nie zależy od przebytej drogi. Praca wykonana po
krzywej zamkniętej jest równa zero – pole spełniające ten warunek
nazywamy zachowawczym.
M
m
m
M
W=0
4. Energia potencjalna w polu grawitacyjnym. Pracę w polu grawitacyjnym ,można obliczyć jako różnicę energii
potencjalnych ciała w poszczególnych punktach pola.
M
Epa
W  E pb  E pa
Epb
W
Epb
m
m
Epb
GMm GMm
GMm
GMm

W  

ra
rb
rb
ra
Ep
Ep  
GMm
 E p  0
r
Ep
r
r
R
Wykres zależności energii
potencjalnej od odległości dla masy
punktowej.
Wykres zależności energii
potencjalnej od odległości dla kuli o
promieniu R.
5. Potencjał pola grawitacyjnego. Jest to stosunek energii potencjalnej ciała umieszczonego w polu do jego masy.
 GMm
Ep
 J   kgm2 1   m 2 
GM
r
V – potencjał grawitacyjny. V 
V
V  
V       2
 2 
m
m
r
 kg   s kg   s 
V
V
r
r
R
Wykres zależności potencjału od
odległości dla kuli o promieniu R.
Wykres zależności potencjału od
.
odległości
dla masy punktowej.
Pracę w polu grawitacyjnym możemy obliczyć stosując potencjał grawitacyjny.
Va
M
Vb
W  E pb  E pa
W  mVb  mVa  W  mVb  Va 
6.Ciężar i siła grawitacji.
Fod
Fg1
Fg=Q
Fg2
Fg
Q
Fg1> Fg2
Fg
Q=Fg-Fod
Na biegunie siła grawitacji jest większa,
niż na równiku gdyż odległość do
środka Ziemi jest tam mniejsza w
stosunku do odległości na równiku.
Siła grawitacji równa jest ciężarowi ciała tylko na
biegunie, ponieważ w innych punktach Ziemi
występuje siła odśrodkowa.
7. Pierwsza prędkość kosmiczna.Jest to prędkość pozwalająca ciłu wejść na orbitę okołoziemską i krążyć wokół
Ziemi.
Fg = Fod
V1
GMm mv 2
GM


 v2
2
R
R
R
GM
g  2  GM  gR 2
R
gR 2
v2 
 v  gR
R
M
R
Fg
Fod
Rysunek z pracy Newtona. Gdy, prędkość rzutu
wzrasta, wzrasta także jego zasięg. Jeżeli F g = Fod
wtedy ciało krąży po orbicie.
v  9,81
R
r
m
m
km
637 10 4 m  7905  7,9
2
s
s
s
Satelita stacjonarny ma okres obiegu 24h i krąży w
płaszczyźnie ziemskiego równika. Orbita
stacjonarna ma promień r=42170km
8.Druga prędkość kosmiczna. Jest to najmniejsza prędkość , którą należy nadać ciału wyrzuconemu z Ziemi, aby
oddaliło się do nieskończoności.
Ep+Ek
R
V2
E p  0
2
2
2
mv
GMm
mv
GMm
v
GM
GM

0



 v2  2
2
R
2
R
2
R
R
2
GM
gR
km
km
g  2  GM  gR 2  v 2  2
 v  2 gR  v 2  2v1  v 2  2  7,9
 11,2
R
s
s
R
E p  E k  E p
E p  Ek  0 
9.Przeciążenie i nieważkość.
a
v
Fb
Q
Stan przeciążenia występuje, w
startującej rakiecie. Na kosmonautę
działają siła bezwładności i ciężar.
FN = Fb + Q
Fg = Fb
Stan nieważkości występuje w satelicie
znajdującym się na orbicie.
Fod
10.Prawa Keplera.
1.Orbita każdej planety jest elipsą przy czym Słońce znajduje się w jednym z jej ognisk.
p
r1
peryhelium
r2
S
aphelium [największa odległość od Słońca]
a
r1 +r2 =a
2.Promień wodzący planety zakreśla w równych odstępach czasu równe pola.
S1 =S2 =S3
S2
S3
S1
3.Drugie potęgi okresów obiegu planet wokół Słońca są wprost proporcjonalne do trzecich potęg ich średnich odległości od
Słońca.
T12 a13

T22 a 23
a1
a2
Jednostka astronomiczna 1AU =149 600 000 km. – średnia odległość Ziemi od Słońca.
Parsek = 206265AU = 3,086 1012 km = 3,262 lat światła.
Rok świetlny = 9,46045 1011 km.
Jeżeli zapoznałeś się z powyższym materiałem oraz znasz i rozumiesz
podstawowe pojęcia, wielkości i prawa związane z działem „grawitacja”
możesz sprawdzić swoje wiadomości rozwiązując dwa umieszczone
poniżej testy.
Rozwiązanie ich pozwoli ci odnaleźć ewentualne braki w twoich
wiadomościach.
Na początku rozwiąż wersję A testu.
Wersja A
1. Układ stanowią dwie jednorodne kule o masach M i m. Wzajemne ich położenie
przedstawia rysunek. Siła wzajemnego oddziaływania tych ciał spełnia zależność:
GMm
a) F 
M
r2
m
GMm
b) F 
R
r  R2
c) F 
d) F 
GMm
r2
GMm
r
r  R2
2. Stała grawitacji w układzie SI jest równa
a) 6,67 10
11
N  m2
c) 9,81
kg 2
N  kg 2
m2
b) 6,67 10
d) 9,81
11
N  m2
kg 2
m
s2
3. Gdyby nagle zniknęła siła powszechnego ciążenia, to spadające swobodnie ciało
a) poruszałoby się ruchem jednostajnym bez zmiany kierunku i zwrotu
b) poruszałoby się ruchem jednostajnym ze zmianą zwrotu na przeciwny
c) przestałoby się poruszać
d) nie zmieniłoby swego ruchu
4. Ciała wytwarzają wokół siebie pole grawitacyjne. Aby można było porównać
właściwości tych pól stosujemy wielkość zwaną
a) przyspieszeniem grawitacyjnym
b) natężeniem pola grawitacyjnego
c) punktową masą próbną
d) energią pola
5. Który ze wzorów pozwala wyliczyć wartość natężenia pola grawitacyjnego Ziemi
w danym punkcie, odległym o r od jej środka:
GMm
GMm
GM
GM
a)
b)
c)
d)
2
2
r
r
m  r2
r
6. Jeżeli w pewnym punkcie pola grawitacyjnego jego natężenie wynosi 1 m/s 2 , to na
umieszczone w tym punkcie ciało o masie 0,5 kg działa siła o wartości
a) 19,6 N
b) 9,8 N
c) 4,9 N
d) 0,5 N
7. Miarą pracy wykonanej przez siłę w polu grawitacyjnym Ziemi jest pole powierzchni
pod krzywą F(r). Który z wykresów umożliwia obliczenie tej pracy? R - promień
Ziemi, r - odległość od jej środka
a)
b)
c)
d)
F
F
F
F
r
R
r
r
R
r
R
R
8. Wartość pracy wykonanej w polu grawitacyjnym nad punktem materialnym, przy
przeniesieniu go po torze zamkniętym jest
a) zależna od kształtu toru, po którym został przeniesiony
b) zależnie od zwrotu działającej siły, większa lub mniejsza od zera
c) równa zeru niezależnie od rodzaju ruchu, jakim przenoszono to ciało
d) równa zeru gdy ciało przenoszono ruchem jednostajnym
9. Praca wykonana przeciwko siłom grawitacji
jest równa zeru przy przemieszczaniu ciała
na odcinku drogi między punktami
a) 1 - 2
b) 2 - 3
c) 3 - 4
d) 4 - 5
1
2
3
M
4
5
10. Wzór na grawitacyjną energię potencjalną ciała znajdującego się w dowolnej
odległości od masy punktowej otrzymujemy z wyrażenia na pracę w polu
grawitacyjnym. Który
z wykresów poprawnie przedstawia zależność Ep(r)?
a)
b)
c)
d)
Ep
Ep R
Ep
Ep
r
R
r
r
r
11. Potencjał pola grawitacyjnego przedstawia
a) stosunek energii potencjalnej ciała umieszczonego w danym punkcie pola do
masy
ciała wytwarzającego to pole
b) pracę, jaką trzeba wykonać, aby ciało o masie jednostkowej przenieść
z powierzchni Ziemi do danego punktu pola
c) energię potencjalną przypadającą na jednostkę masy ciała znajdującego się
w danym punkcie pola
d) pracę, którą trzeba wykonać, aby ciało o masie jednostkowej przenieść
z powierzchni Ziemi do nieskończoności
12. Potencjał pola grawitacyjnego ma w każdym punkcie pola
a) inną wartość
b) wartość równą zero
c) wartość większą od zera
d) wartość mniejszą od zera
13. Newton wykazał, że prawa Keplera wynikają z prawa powszechnej grawitacji. Która
z poniższych zależności pozwala wyprowadzić III prawo Keplera?
G  M  m 4  2  m
b)

r2
r2
G  M  m m  v2
d)

T
r2
GMm mv
a)

r
r2
G  M  m 4  2  r  m
c)

r2
T2
14. Znając doświadczalnie wyznaczoną stałą grawitacji podaj, które z poniższych danych
należy jeszcze znać, aby wyznaczyć masę Ziemi?
a) okres obiegu Ziemi wokół Słońca
b) przyspieszenie ziemskie i promień Ziemi
c) okres obrotu Ziemi wokół własnej osi
d) przyspieszenie ziemskie i masę ciała umieszczonego na Ziemi
15. Prędkość liniowa satelity stacjonarnego poruszającego się po orbicie o promieniu
r1 = 42 245 km ma wartość v1,a satelity „bliskiego” poruszającego się po orbicie
kołowej o promieniu r2 = 6700 km ma wartość v2. Okres obiegu satelity stacjonarnego
T1 jest większy od okresu T2 satelity „bliskiego”, ponieważ
a) v1 < v2 i 2r1 > 2r2
b) v1 = v2 i r1 > r2
r
v
c) v1 > v2 ale 1  1
d) v1 < v2 ale 1 > 2
r2 v 2
16. Pojazd wysłany na Marsa z odległości r od środka Ziemi ( M - masa Ziemi ) musi
przed wyłączeniem silników osiągnąć prędkość równą
a)
GM
r
b)
2GM
r
c)
GM
r
d)
2GM
r
17. Dwa pojazdy kosmiczne krążą wokół Ziemi po orbitach kołowych r i 2r. Które
z powyższych informacji są prawdziwe?
1) Stosunek energii kinetycznej do potencjalnej jest inny dla każdego z nich.
2) Stosunek energii kinetycznej do potencjalnej jest dla obu taki sam.
3) Prędkość satelity bardziej odległego od Ziemi jest mniejsza od prędkości satelity
poruszającego się bliżej Ziemi.
4) Prędkość satelity bardziej odległego od Ziemi jest większa od prędkości satelity
poruszającego się bliżej Ziemi.
Prawdziwe są tylko:
a) 1 i 3
b) 2 i 3
c) 2 i 4
d) 1 i 4
18. W szklanym naczyniu znajduje się cienka warstwa rtęci. Jak zachowa się rtęć
jeśli naczynie znajdzie się w stanie nieważkości?
a) przyjmie kształt kulisty
b) oderwie się od dna i będzie się nad nim unosić bez zmiany kształtu
c) nie zmieni swego położenia ani kształtu
d) ulegnie rozdrobnieniu na dużą liczbę drobnych cząstek o dowolnych kształtach
19. Masa Słońca zmienia się ustawicznie wskutek promieniowania olbrzymich ilości
energii i cząstek elementarnych. Powinno to być przyczyną
a) zwiększania się okresów obiegu planet wokół Słońca bez zmiany ich średnich
odległości od niego
b) zmniejszania się okresów obiegu planet wokół Słońca bez zmiany ich średnich
odległości od niego
c) zwiększenia się średnich odległości planet od Słońca i wzrostu ich okresów
obiegu
wokół niego
d) zwiększenia się średnich odległości planet od Słońca i zmniejszania się ich
okresów obiegu wokół niego
20. Która z poniższych sytuacji pozwala zaobserwować przeciążenie i nieważkość?
a) w stanie nieważkości znajduje się skoczek spadochronowy lecąc z zamkniętym
spadochronem, po jego otwarciu skoczek znajduje się w stanie przeciążenia
b) lecąc myśliwskim samolotem odrzutowym na dużej wysokości pilot jest w stanie
nieważkości, przy każdej zmianie wysokości pilot doznaje przeciążenia
c) w stanie nieważkości znajduje się skoczek spadochronowy lecąc z otwartym
spadochronem, podczas lądowania doznaje przeciążenia
d) w czasie skoku do wody skoczek odbija się od trampoliny będąc w stanie
przeciążenia, a w chwili osiągnięcia największej wysokości skoczek jest w stanie
nieważkości
Teraz porównaj swoje odpowiedzi z tabelą odpowiedzi prawidłowych.
Numer
1
pytania
Prawidłowa c
odpowiedź
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20
b
a
b
c
d
a
d
b
b
c
d
c
b
a
d
b
a
c
d
Sprawdź teraz na jakie pytania odpowiedziałeś źle i odszukaj w materiale treści związane
z tymi pytaniami.
Przeanalizuj jeszcze raz te wiadomości i popraw popełnione błędy.
Teraz możesz rozwiązać wersję B testu.
Wersja B
1. Układ stanowią dwie jednorodne kule, których położenie przedstawiają rysunki. Który
układ ciał poprawnie ilustruje poniższe wyrażenie na wartość siły grawitacji?
F
x
a)
M
m
x
M
R
 x  r 2
b)
r
R
c)
GMm
M
x
r
R
x
d)
m
r
m
M
R
m
r
2. Stała grawitacji w układzie SI liczbowo jest równa
a) sile z jaką działają na siebie punktowe ciała o masie m1 = m2 = 1 kg umieszczone
w odległości 1 m od siebie
b) sile z jaką Ziemia przyciąga ciało o masie 1 kg
c) przyspieszeniu grawitacyjnemu
d) sile grawitacji z jaką przyciągają się w próżni dwa ciała o łącznej masie 1 kg
z odległości 1 m
3. Gdyby nagle zniknęło powszechne ciążenie , to Księżyc poruszałby się
a) w dalszym ciągu po orbicie kołowej wokół Ziemi
b) po linii spiralnej oddalając się od Ziemi
c) po linii prostej oddalając się od Ziemi
d) po linii krzywej opadając na Ziemię
4. Przez natężenie pola grawitacyjnego w danym punkcie pola rozumiemy
a) siłę działającą na ciało o masie M umieszczone w danym punkcie pola
b) siłę grawitacji przypadającą na jednostkę masy ciała umieszczonego w danym
punkcie pola
c) przyspieszenie grawitacyjne w tym punkcie
d) energię potencjalną przypadającą na jednostkę masy ciała znajdującego się
w danym punkcie pola
5. Która z podanych jednostek odnosi się do natężenia pola grawitacyjnego?
kg  m 2
a)
s2
b)
m
s2
c)
N
m
d)
kg
s2
6. Natężenie pola grawitacyjnego w danym punkcie tego pola zależy od
a) obszaru zajmowanego przez pole
b) masy ciała znajdującego się w tym polu
c) masy ciała wytwarzającego to pole
d) masy ciała będącego źródłem pola oraz odległości tego punktu od źródła pola
7. Ciężar danego ciała na Ziemi jest
a) największy na biegunie
c) niezależny od szerokości geograficznej
b) wszędzie jednakowy
d) największy na równiku
8. Początkowa odległość dwóch punktów materialnych o masie M i m wynosi r. Wartość
pracy potrzebnej do oddalenia ich na odległość nieskończenie dużą jest
a) również nieskończenie duża
c) równa zeru
GMm
r2
GMm
d) równa
r
b) równa
9. Przez potencjał pola grawitacyjnego rozumiemy
a) stosunek natężenia pola do przyspieszenia grawitacyjnego w danym punkcie pola
b) energię potencjalną przypadającą na jednostkę masy ciała znajdującego się
w danym punkcie pola
c) pracę jaką trzeba wykonać, aby ciało o jednostkowej masie przenieść
z powierzchni Ziemi do danego punktu pola
d) stosunek energii potencjalnej ciała umieszczonego w danym punkcie pola do
masy ciała wytwarzającego to pole
10.Ciało o masie m przenoszono w polu grawitacyjnym
z punktu K do L po trzech różnych torach
oznaczonych na rysunku literami a, b, c. Który
z poniższych sądów jest prawdziwy?
a) najmniejszą pracę nad tym ciałem wykonano
przenosząc je po torze b
b) największą pracę nad tym ciałem wykonano
przenosząc je po torze c
c) prace wykonane nad tym ciałem na wszystkich
torach są jednakowe
d) prace wykonane nad tym ciałem na wszystkich
torach są równe zeru
K
b
a
c
L
11.Grawitacyjna energia potencjalna układu mas (punktów materialnych)
a) zawsze zwiększa się podczas wzrostu wzajemnej odległości tych mas
b) wzrasta lub maleje, np. jeśli umówimy się, że energia potencjalna tych dwóch
punktów materialnych przy wzajemnej odległości równej Ro jest równa zeru, to
przy ich odsuwaniu dla r > Ro energia potencjalna układu
maleje, a dla r < Ro
energia potencjalna wzrasta
c) maleje podczas wzrostu ich wzajemnej odległości, jeżeli przyjmiemy umowę, że
energia potencjalna tego układu będzie równa zeru, gdy ciała rozsuniemy na
odległość nieskończenie wielką
d) zawsze maleje podczas wzrostu wzajemnej odległości tych mas
12.Potencjał V = V ( r ) pola grawitacyjnego Ziemi poprawnie przedstawia wykres
a)
b)
c)
d)
V
V R
V
V
r
r
R
r
r
13.Znając doświadczalnie wyznaczoną stałą grawitacji podaj, które z poniższych danych
należy jeszcze znać, aby wyznaczyć masę Słońca?
a) okres obrotu Ziemi wokół własnej osi i masę Ziemi
b) przyspieszenie ziemskie i promień Ziemi
c) okres obiegu Ziemi wokół Słońca i odległość Ziemia - Słońce
d) przyspieszenie ziemskie i okres obrotu Ziemi wokół własnej osi
14.Gdyby Księżyc miał 2 razy większą masę i znajdował się 2 razy dalej od Ziemi, to siła
wzajemnego przyciągania tych ciał
a) zmalałaby 4 razy
b) zmalałaby 2 razy
c) zwiększyłaby się 4 razy
d) zwiększyłaby się 2 razy
15.Gdyby prędkość stacjonarnego satelity Ziemi nagle wzrosła do wartości mniejszej od
vII (gdzie vII jest drugą prędkością kosmiczną), to satelita
a) odleciałby na zawsze od Ziemi, stając się satelitą Słońca
b) poruszałby się dalej po tej samej orbicie ale z większą prędkością
c) poruszałby się po orbicie o większym promieniu
d) poruszałby się po orbicie eliptycznej
16.Dwie stacje kosmiczne krążą wokół Ziemi: jedna w odległości 300 km, a druga
w odległości 400 km od jej powierzchni. Na tej podstawie można powiedzieć, że
a) druga prędkość kosmiczna stacji bliższej jest większa
b) druga prędkość kosmiczna stacji dalszej jest większa
c) ich prędkości ucieczki z pola grawitacyjnego Ziemi mają jednakowe wartości
d) trudno określić prędkość ucieczki na podstawie tych danych
17.Sztuczny satelita okrążający Ziemię po orbicie eliptycznej porusza się coraz prędzej
gdy zbliża się do Ziemi, a coraz wolniej gdy się od niej oddala. Jego całkowita energia
mechaniczna względem układu związanego z Ziemią jest
a) największa w punkcie najbliższym Ziemi
b) największa w punkcie najbardziej odległym od Ziemi
c) jednakowa we wszystkich punktach toru
d) największa w tym punkcie, w którym jego ruch zmienia się z przyspieszonego
na opóźniony
18.Dwa ciała o masie m i 5m zbliżają się do siebie na skutek oddziaływania
grawitacyjnego (wszystkie inne siły zaniedbujemy). Co można powiedzieć
o przyspieszeniu tych ciał?
a) przyspieszenia chwilowe ciał mają takie same wartości, ale przeciwne zwroty,
wartości obu przyspieszeń wzrastają z upływem czasu
b) w każdej chwili wartość przyspieszenia ciała lżejszego jest 5 razy większa niż
wartość przyspieszenia ciała cięższego
c) wartość przyspieszenia ciała lżejszego jest 5 razy większa od wartości
przyspieszenia ciała cięższego, a ponadto wartość każdego z tych przyspieszeń
jest niezmienna w czasie
d) przyspieszenia chwilowe tych ciał są stałe
19.Stan nieważkości w rakiecie lecącej na Księżyc pojawi się gdy
a) osiągnie ona pierwszą prędkość kosmiczną
b) osiągnie ona drugą prędkość kosmiczną
c) ustanie praca silników
d) osiągnie ona punkt równowagi przyciągania Ziemi i Księżyca
20.Które z wymienionych praw obowiązuje w warunkach nieważkości?
a) prawo Pascala
b) prawo Archimedesa dla gazów
c) prawo Archimedesa dla cieczy
d) prawo równowagi cieczy w naczyniach połączonych
Teraz porównaj swoje odpowiedzi z tabelą odpowiedzi prawidłowych.
Numer
1
pytania
Prawidłowa d
odpowiedź
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20
a
c
b
b
d
a
d
b
c
a
a
c
b
d
a
Ocena wyników twojej pracy
ILOŚĆ UZYSKANYCH PUNKTÓW
OCENA
18 - 20
17 - 15
14 - 12
11 - 9
8 i mniej
5
4
3
2
1
c
b
c
a
Zastosowanie tego opracowania na lekcjach powtórzeniowych powinno
pomóc uczniom w zrozumieniu problemów związanych z polem
grawitacyjnym.
Umożliwia ono także samodzielne powtórzenie materiału uczniom
klas maturalnych, którzy przygotowują się do egzaminów wstępnych
z fizyki.
Mamy nadzieję, że materiały zawarte w tym opracowaniu ułatwią
uczniom poznanie praw i zjawisk związanych z polem grawitacyjnym.
Cezary Misztela
Marek Pleszczyński