Równania Keplera dla orbit eliptycznych
Pole grawitacyjne jest polem „zachowawczym” – suma energii potencjalnej
i kinetycznej ciała, o ile nie działają inne siły, pozostaje stała
1 2 GMm
mv
E const
2
r
(1)
Wprowadzając współrzędne polarne (r, φ) , składowa radialna prędkości wynosi
vr v cos
a składowa kątowa
v v sin r
dr
dt
d
dt
(2 )
(3 )
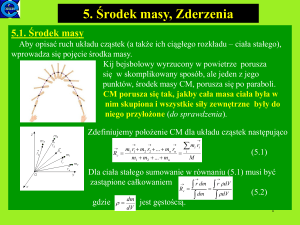
gdzie r jest „promieniem wodzącym” planety a α kątem między wektorem
prędkości a prostopadłą do promienia wodzącego
We współrzędnych polarnych prawo zachowania energii przyjmuje postać:
2
2
1 dr d
GMm
E
r
2 dt dt
r
(4 )
Prawo zachowania momentu pędu określa stałość iloczynu wektorowego
r x p = const, co we współrzędnych polarnych
p rm sin
(5)
a uwzględniając (3)
d
p rm r
dt
(6)
skąd otrzymujemy
d
p
dt
mr 2
(7)
podstawiając powyższe wyrażenie do prawa zachowania energii (4)
otrzymujemy
2
1 dr
p2
GMm
m 2 2 E
2 dt m r
r
(8 )
Po przekształceniach
2
p2
2 E 2GM
dr
2 2
m
r
dt m r
dr
2 E 2GM
p2
2 2
dt
m
r
mr
(9 )
(10 )
Podstawiamy teraz wyrażenie (10) do równania (7)
d d dt
p
dr dt dr mr 2
1
2 E 2GM
p2
2 2
m
r
m r
(11)
czyli
d
dr
r2
b
2a b 2
1
r r2
(12 )
gdzie dokonaliśmy podstawień
Równania Keplera dla orbit eliptycznych
2
b2
p2
2 Em
p2
2 Em
GMm
a
2E
b
( 13 )
Całkując (przez części) równanie (12 ) otrzymujemy
0 arc cos
b 2 ar
(14 )
r a 2 b2
Równanie (12) jest równaniem elipsy, o czym można się przekonać dokonując
podstawienia
czyli
cos
b 2 ar
r a 2 b2
( 15 )
b 2 r ( a a 2 b 2 * cos )
Równanie powyższe jest równaniem (parametrycznym) elipsy o dłuższej półosi
a i krótszej b.
POTENCJAŁ EFEKTYWNY
Ogólnie, trajektorie w polu grawitacyjnym są krzywymi stożkowymi –
okręgiem, elipsą, parabolą, hiperbolą, w zależności od prędkości ciała (komety,
planety)
Na poruszające się ciało w polu grawitacyjnym działa siła przyciągania plus siła
(pozorna) odśrodkowa
GMm
d
Fr 2 m
r
r
dt
2
( 16 )
podstawiając z równania (7) dφ/dr otrzymujemy
Fr
GMm p 2
3
r2
mr
( 17 )
a całkując to wyrażenie po dr
dostajemy następujące wyrażenie na potencjał (efektywny) oddziaływania
Równania Keplera dla orbit eliptycznych
3
GMm
p2
U ef (r )
r
2mr 2
( 18 )
Wykres tego potencjału przedstawia poniższy rysunek
Pojęcie potencjału efektywnego wyjaśnia, kształt orbit. Jeśli planeta ma energię
całkowitą odpowiadającą minimum potencjału, to jej odległość od Słońca jest
stała (ruch po okręgu). Jeśli energia jest nieco wyższa, to odległość się zmienia,
między minimum aphelium a maksimum perihelium (czyli jest eliptyczna).
Jeśli energia wynosi zero (czyli ciało nadlatuje z „nieskończoności”, jak komety
z obłoku Oortsa), to orbita jest paraboliczna, jeśli jest większa niż zero, to
hiperboliczna.
Równania Keplera dla orbit eliptycznych
4