Wykład 5

5. Środek masy, Zderzenia
5.1. Środek masy
Aby opisać ruch układu cząstek (a także ich ciągłego rozkładu – ciała stałego),
wprowadza się pojęcie środka masy.
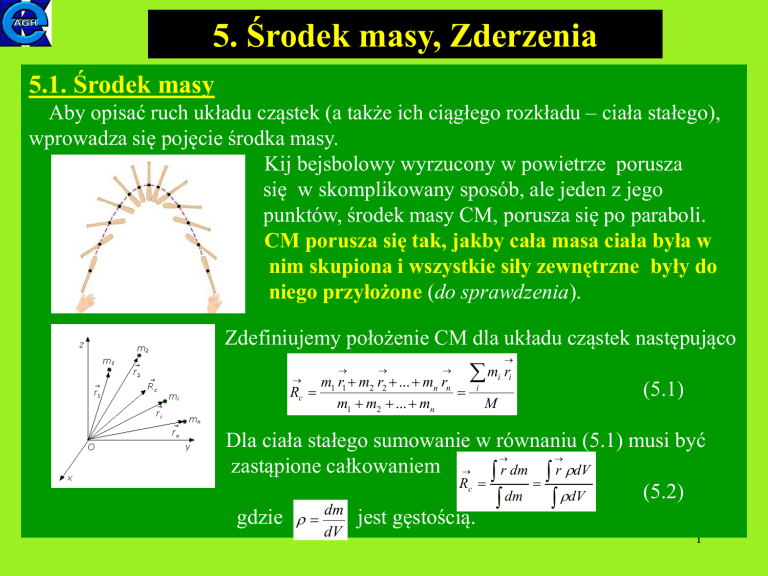
Kij bejsbolowy wyrzucony w powietrze porusza
się w skomplikowany sposób, ale jeden z jego
punktów, środek masy CM, porusza się po paraboli.
CM porusza się tak, jakby cała masa ciała była w
nim skupiona i wszystkie siły zewnętrzne były do
niego przyłożone (do sprawdzenia).
Zdefiniujemy położenie CM dla układu cząstek następująco

Rc 




m1 r1  m2 r2  ...  mn rn

m1  m2  ...  mn
 mi ri
(5.1)
i
M
Dla ciała stałego sumowanie w równaniu (5.1) musi być
zastąpione całkowaniem
 r dm   r dV
R 
(5.2)
dm
dV


gdzie   dm jest gęstością.



c
dV
1
Środek masy, c.d.
Dla ciała jednorodnego (ρ=const), położenie CM zależy tylko od kształtu ciała


Rc 
  r dV
  dV


 r dV
 dV
(5.3)
Przykłady
1. Dwie cząstki o masach m1 i m2 w odległości wzajemnej d.
Położenie CM znajdujemy umieszczając obie cząstki na osi x .
Z równania (5.1) otrzymuje się
xC 
m1 x1  m2 x 2 m1 x1  m2 ( x1  d )

m1  m2
m1  m2
Przyjmując x1=0 otrzymuje się
xC 
m2 d
m1  m2
2. Środek masy trójkąta.
W tym przypadku zamiast stosowania równania (5.3), można
podzielić trójkąt na małe paski równolegle do każdego z boków.
Środek masy każdego paska leży w jego połowie. Dochodzimy ostatecznie do
2
wniosku, że przecięcie środkowych boków trójkąta wyznacza jego CM.
5.2. Ruch układu cząstek
Dla układu n cząstek można zapisać równanie (5.1) następująco



(5.4)

MRc  m1 r1  m2 r2  ...  mn rn
Różniczkując obie strony równania (5.4) po czasie otrzymuje się




M v C  m1v 1  m 2 v 2  ...  mn v n
(5.5)
Różniczkując ponownie po czasie równanie (5.5) mamy




M aC  m1 a1  m2 a2  ...  mn an
(5.6)
Równanie (5.6) może być zapisane następująco




M aC  F1  F2  ...  Fn
(5.6a)
W skład prawej strony równania (5.6a) wchodzą wszystkie siły, zarówno
wewnętrzne działające między cząstkami, jak i siły zewnętrzne. Z III zasady
dynamiki Newtona suma wszystkich sił wewnętrznych jest równa zero, gdyż
występują one parami, a zatem prawa strona równania (5.6a) jest wektorową sumą
sił zewnętrznych, siłą wypadkową. W tym przypadku otrzymuje się:
(5.7)

Fnet  m aC
II zasada dynamiki zastosowana do układu mas
To potwierdza założenie poczynione na początku paragrafu.
3
5.3. Pęd układu cząstek
Równanie (5.5) można zapisać następująco




M v C  p1  p2  ...  pn
(5.8)
A zatem pęd wypadkowy układu cząstek (prawa strona powyższego równania)
jest równy iloczynowy masy całkowitej układu i prędkości środka masy


(5.9)
Mv  P
C
Różniczkując równanie (5.9) względem czasu otrzymuje się



dv C dP
M

 MaC
dt
dt
(5.10)
Z powyższej zależności, po uwzględnieniu równania (5.7) otrzymuje się


dP
Fnet 
dt
Na
Pęd układu zmienia się na skutek działania sił zewnetrznych
(5.11)
(druga zasad Newtona dla układu cząstek).

podstawie (5.11) wnioskujemy, że jeżeli Fnet jest równe zero, zatem

P  const
Dla izolowanego układu jego pęd nie zmienia się
(prawo zachowania pędu dla układu cząstek).
(5.12)
4
Pęd układu, przykład
Stojący na lodzie łyżwiarz A w pewnym momencie odpycha od siebie innego
łyżwiarza B, który zaczyna się poruszać z prędkością 3 m/s. Jaki jest kierunek
i wartość prędkości początkowej łyżwiarza A? Masy łyżwiarzy wynoszą
mA = 100 kg, mB = 60 kg.
Pęd układu w chwili początkowej wynosił zero i ponieważ zadziałały siły
wewnętrzne, więc się nie zmienił.


m A v A  mBv B  0
Skierowując te wektory wzdłuż osi x można napisać
m Av A  mBv B  0
lub
vA  
mBv B
 1,8 m / s
mA


Tzn. wektor v A ma przeciwny zwrot niż v B .
5
5.4. Zderzenia
Pęd ciała można zmienić w wyniku zderzenia z innym. Przykładem może być
uderzenie kija bejsbolowego w piłkę. Siły działające podczas zderzenia są duże
i działają krótko.
Na podstawie drugiej zasady dynamiki można zapisać
 
dp  F ( t ) dt
(5.13)
Całkując równanie (5.13) w przedziale czasu Δt = tf – ti otrzymuje się zmianę pędu
 tf 
 dp   F ( t ) dt
tf
ti
ti
lub
 tf 
 p   F ( t ) dt
(5.14)
ti
Zmiana pędu ciała jest równa popędowi siły.
Na rys. po lewej pokazana jest zmiana w czasie siły z jaką
oddziałuje kij bejsbolowy na piłkę.
Pole powierzchni pod krzywą F(t) jest równe wartości
popędu doznawanego przez piłkę podczas zderzenia.
6
Zderzenia, cd.
W wielu przypadkach mamy do czynienia z układami izolowanymi, w których
ciała zderzają się wzajemnie. W takim przypadku pęd układu nie zmienia się
i niezależnie od rodzaju zderzenia suma pędów zderzających się ciał pozostaje
stała.
Gdy energia kinetyczna układu po zderzeniu nie zostaje zachowana to nazywamy
je niesprężystym. W przeciwnym przypadku zderzenie jest sprężyste.
Zderzenie całkowicie niesprężyste w jednym wymiarze
Zderzenie traktujemy jako całkowicie niesprężyste gdy dwa ciała po zderzeniu
nie rozdzielają się. W przypadku zderzenia w jednym wymiarze ruch ciał przed
i po zderzeniu odbywa się wzdłuż jednej linii prostej. Z prawa zachowania pędu
można napisać (ponieważ ruch jest jednowymiarowy nie musi się stosować zapisu
wektorowego):
m1v1  m2v 2  ( m1  m2 )u
(5.15)
7
Zderzenia, cd.
a zatem prędkość połączonych ciał po zderzeniu jest równa:
u
m1v1  m2v 2
m1  m2
(5.16)
Łatwo sprawdzić, że energia kinetyczna mas po zderzeniu jest mniejsza niż suma
ich energii kinetycznych przed zderzeniem.
Zderzenie sprężyste w jednym wymiarze
Korzystając z praw zachowania pędu i energii kinetycznej można zapisać
(5.17)
m1v1  m2v 2  m1u1  m2u2
m1v12 m2v 22 m1u12 m2u22



2
2
2
2
(5.18)
Rozwiązując układ równań (5.17) i (5.18) można wyznaczyć prędkości u1 i u2
po zderzeniu
u1 
m1  m2
2m2
v1 
v2
m1  m2
m1  m2
u2 
2m2
m  m2
v1  1
v2
m1  m2
m1  m2
Gdy cząstki mają te same masy, wymieniają
prędkości po zderzeniu
8
Zderzenia, cd.
Zadanie
Na rys. poniżej masa m2 znajduje się w spoczynku na gładkim stole i jest
przymocowana do ściany za pomocą sprężyny o stałej sprężystości k.
Masa m1 poruszająca się z prędkością v1 zderza się z masą m2 i obie masy
łączą się napinając sprężynę. Gdy masy te na moment się zatrzymują, to o ile
skróciła się wtedy sprężyna?
Z zasady zachowania pędu
otrzymuje się:
m1v1  ( m1  m2 )u0
u0 
m1v1
m1  m2
u0 – prędkość w momencie rozpoczęcia sprężania
Energia kinetyczna układu mas zamienia
się w energię potencjalną sprężyny
m1  m2 u02
kx 2
2
2
m1  m2
x  u0

k

m1v1
m1  m2 k
9
5a. Grawitacja
5a.1. Prawo powszechnego ciążenia
Dwie cząstki przyciągają się wzajemnie siłami grawitacji, z których każda jest
proporcjonalna do iloczynu ich mas. Prawo to sformułował Newton w postaci:
mm
F  G 12 2
r
F12
m1
m1 i m2 – masy cząstek
r – odległość między cząstkami
G = 6.67 · 10-11 Nm2/kg2 - stała grawitacyjna
F21
^r
r



m2

F 12   F 21 r / r  r

r  wektor jednostkowy o wartości 1
Prawo grawitacji można zapisać w postaci wektorowej

F 21  G
m1 m 2 
r
2
r
(5.19)
Chociaż prawo to stosuje się ściśle do punktowych cząstek, można je stosować
również do obiektów rzeczywistych z rozmiarami małymi w porównaniu do
odległości między nimi. Można je także stosować do mas o symetrii sferycznej.
10
5a.2. Przyciąganie grawitacyjne Ziemi
Ziemia przyciąga masę m położoną w odległości r od jej środka siłą
F G
m MZ
r2
(5.20)
m
r
Siła grawitacji F powoduje spadanie masy m
w kierunku środka Ziemi z przyspieszeniem
ag 
M
F
MZ
 G 2Z  G
m
r
( RZ  h ) 2
F
RZ
(5.21)
MZ
Przyspieszenie grawitacyjne zmienia się z wysokością h = r – RZ nad
powierzchnią Ziemi. Z równania (5.21) otrzymuje się :
h (km) ag (m/s2)
0
9.83
400
8.70
35700 0.225 (sat. telekom.)
Musimy jednak mieć na uwadze, że Ziemia nie jest kulista (bardziej podobna do
elipsoidy obrotowej spłaszczonej na biegunach), jej gęstość nie jest stała i obraca
się wokół osi. Zatem założenie, że w każdym miejscu na powierzchni Ziemi
g = 9.8 m/s2 jest uproszczeniem. W ogólności g jest mniejsze na równiku od 11ag
wg. wzoru (5.21) o 0.034m/s2 .
5a.3. Ruch planet i satelitów
Do analizy tego ruchu stosuje się zasady dynamiki Newtona i prawo powszechnej
grawitacji.
Na rys. obok dwa obiekty o porównywalnych masach obracają się wokół
wspólnego środka masy C. Mają te same prędkości kątowe ω.
Z trzeciej zasady dynamiki siły dośrodkowe działające na
każdą z mas są sobie równe i równe sile grawitacji
r
mv 12 Mv 22

albo m 2r  M 2R
r
R
GMm
m r 
( R  r )2
2
gdzie  
2
T
R
(5.22)
C

(5.23)
m
F
M

F
Dla układu gwiazda planeta masa gwiazdy jest znacznie większa niż planety
(M>>m), stąd R<<r. W tym przypadku z (5.23 ) otrzymuje się
GM   r
2
3
albo GM 
4 2
T
r3
(5.24)
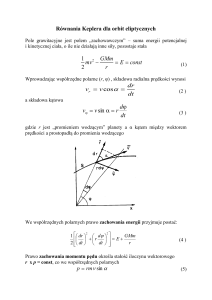
W ogólności planety poruszają się po orbitach eliptycznych z gwiazdą, np. Słońce,
w jednym z ognisk (pierwsze prawo Keplera) i w tym wypadku w miejsce r w12
równaniu (5.24) podstawia się półoś dużą elipsy a.
2
Ruch planet i satelitów, cd.
Zalezność między T2 i r3 otrzymana z (5.24) jest również znana jako tzw. III prawo
Keplera. Z zależności tej można określić masę gwiazdy gdy znane są T oraz r dla
orbitującej planety.
Równ. (5.24) może być również użyte do analizy ruchu satelitów wokółziemskich
(w tym wypadku podstawiamy M = MZ).
Przykład
Stosując równ. (5.24) wyznaczyć promień orbity satelity geostacjonarnego, który
wydaje się nieruchomy dla obserwatora na powierzchni Ziemi.
Wnioskujemy, że w tym wypadku płaszczyzna orbity satelity musi leżeć w
płaszczyźnie równika.
(5.25)
4 2 3
GM Z 
T2
r
gdzie T  24 godz
Z (5.25) wyznacza się r
r
3
GM ZT 2
4 2
(5.26)
Po podstawieniu wymaganych danych otrzymuje się dla r ok. 42 000 km.
13
5a.4. Grawitacyjna energia potencjalna
Siła grawitacji jest typową siłą zachowawczą. W rozdz. 4.4 wprowadzono wyrażenie
na energię potencjalną w punkcie B danym wektorem r w odniesieniu do energii
potencjalnej UA w punkcie A
m
dr
r



U  r   U A   FC  dr
 
A
r
F(r)
B
RZ
Zakładając, że UA= 0 dla r = ∞ otrzymuje się wyrażenie
na energię potencjalną cząstki w polu sił zachowawczych
MZ
r

 
U  r     FC  dr
 

(5.27)
Jeżeli źródłem siły zachowawczej FC jest Ziemia otrzymuje się z (5.27)
r
r
GMm  
GMm
GMm

U  r     (  3 ) r  dr   2 dr  
r
r
r
 


r


GMm
r
(5.28)
Równ. (5.28) jest wyrażeniem na energię potencjalną masy m w polu grawitacyjnym
masy M (ściśle jest to energia potencjalna układu dwu mas).
14
Grawitacyjna energia potencjalna, cd.
Prędkość ucieczki
Z jaką prędkością początkową należy z powierzchni Ziemi wystrzelić pionowo
pocisk aby nie wrócił na Ziemię.
Z równ. (5.28) wynika, że w nieskończoności energia potencjalna pocisku jest równa
zero. W nieskończoności pocisk się zatrzymuje, zatem jego energia kinetyczna
również osiągnie wartość zerową. Całkowita energia mechaniczna w
nieskończoności jest więc równa zero. Z zasady zachowania energii mechanicznej
wynika, że suma energii kinetycznej i potencjalnej na powierzchni Ziemi jest równa
sumie tych energii w nieskończoności, czyli zero.
mv02 GM Z m

 00
2
RZ
(5.29)
W wyniku otrzymuje się
v0 
2GM Z
 11.2 km / s
RZ
(5.30)
Z (5.30) można wyliczyć prędkość ucieczki z dowolnego obiektu astronomicznego.
Dla gwiazdy neutronowej otrzymuje się prędkość rzędu 105 km/s.
15
Energia w ruchu orbitalnym
Satelita o masie m porusza się po orbicie radialnej wokół
Ziemi o masie M . Ponieważ M >> m, możemy przypisać
energie kinetyczną i potencjalną tylko satelicie.
Energia potencjalna jest dana równ. (5.28):
U (r )  
r
m
M
GMm
r
Energia kinetyczna może być znaleziona z warunku, że siłą
dośrodkową w ruchu satelity jest siła grawitacji
GMm mv 2

r2
r

mv 2 GMm

2
2r
(5.31)
Całkowita energia mechaniczna jest zatem równa
(5.32)
GMm GMm
GMm
E U E  


0
k
r
2r
2r
Energia całkowita jest ujemna co oznacza, że orbita jest
zamknięta.
16
Energia w ruchu orbitalnym, cd.
W ruchu po orbicie eliptycznej, zamieniamy
promień okręgu r w równ. (5.32) na półoś dużą a
elipsy.
Podczas ruchu po orbicie eliptycznej energie
kinetyczna i potencjalna zmieniają się periodycznie
ale całkowita energia mechaniczna jest zawsz stała.
Elipsa z półosią dużą a
i mimośrodem e. Słońce o masie
M znajduje się w ognisku elipsy F.
Energia całkowita orbitującego obiektu zależy
tylko od wartości półosi dużej a orbity eliptycznej
a nie od wartości mimośrodu e.
Dwie orbity: kołowa i eliptyczna, gdzie
promień okręgu jest równy półosi dużej a.
17