Fizyka plazmy

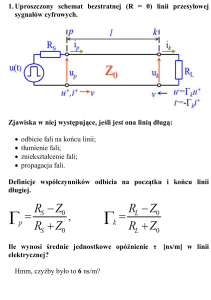
PLAZMA
Elektrony
kwazineutralność
Zjonizowany gaz
ne  ni
Jony
np. wysokotemperaturowa
plazma wodorowa
(całkowicie zjonizowana)
  E  4
jeśli np.
4n  e  E
E
x
E
x  1mm T  300K
n  7 1016
to:
4nex
V
E  10
cm
10
jonów i eletronów / cm 3
,
  109V
Drastyczne odstępstwa od kwazineutralności są natychmiast
likwidowane przez powstające pola elektryczne
Nierealne!
Promień Debye’a
rD
W dostatecznie małych obszarach kwazineutralność może być naruszona
Istnieje pewien charakterystyczny parametr określający liniowe rozmiary
takiego obszaru
x
rD
x
rozdzielenie ładunków zachodzi
bez istotnego wpływu na ruch
cząstek
rD
kwazineutralność praktycznie zachowana
rD
oszacujmy rD
U  e
4ne r
2 2
D
rD
T
PLAZMA: zjonizowany gaz,
dla którego: r
L
T
4ne 2
definicja Langmuria
D
 qe
r

r
rD
Dwa słowa o temperaturze:
na ogół:
Te
Ti
Te , Ti
OSCYLACJE (DRGANIA) PLAZMY

me x  eE x  4e 2 x
4ne 2
p 
me
w oscylacjach jony praktycznei nie
uczestniczą
oscylacje plazmowe - Langmuira
Rolę siły „przywracającej” pełni przede wszystkim długozasięgowe
pole elektryczne (w zwykłym gazie gradient ciśnienia)
Oscylacje plazmowe mogą propagować się w plazmie jako tzw. fale plazmowe (Langmuira)
z częstością    p
Dokładniej (uwzględniając również efekt ciśnienia):
pe
  k
 e
2
2
p
2
e  nme
i uwzględniając, że jest to proces adiabatyczny (zmiany ciśnienia)
Cp
praktycznie tylko dla jednego stopnia swobody
( 
 3 ,a nie 5/3):
CV
2
3
k
Te
2
2
  p 
me
Tłumienie fali:
1) ZDERZENIA (KOLIZJE) (tarcie)
2) MECHANIZM LANDAUA (tłumienie bezkolizyjne)
dla dużych k tłumienie Landaua jest tak duże, że
przedłużanie krzywej nie ma fizycznego sensu
TŁUMIENIE LANDAUA – pierwsze podejście
ϕ(x)
u1  v1  v f  0
FALA PLAZMOWA
PORUSZAJĄCA SIĘ
Z PRĘDKOŚCIĄ Vf
(w prawo)
1
ϕ0
2
u 2  v2  v f  0
Przechodzimy do układu poruszającego się wraz z falą!
ϕ(x) – sekwencja studni potencjału
v - prędkość elektronu w układzie laboratoryjnym
u  v  v f - prędkość w układzie fali
meu 2
e0
2
ELEKTRONY ZŁAPANE W STUDNI POTENCJAŁU – elektrony „rezonansowe”
(stanowią one wąski przedział v w spektrum prędkości, gdyż na ogół e 0 jest
małe w porównaniu z energią cieplną elektronów
Dwie grupy cząstek
rezonansowych:
1) Doganiające falę
v v f
2) Wolniejsze od fali
v v f
w układzie fali zderzenia są sprężyste, dlatego w
układzie laboratoryjnym PO zderzeniu ze ścianką:
v1'  v f  v1  v f  v1
elektron stracił energię, więc została
ona oddana fali
v2'  v f  v2  v f  v2
elektron zyskał energię kosztem
energii fali
PONIEWAŻ ELEKTRONÓW
WOLNIEJSZYCH JEST WIĘCEJ,
SUMARYCZNY EFEKT PROWADZI
DO ZMIANY ENERGII FALI NA
ENERGIĘ CIEPLNĄ ELEKTRONÓW
(TŁUMIENIE FALI)
DEKREMENT TŁUMIENIA
1 d
 

2 dt
def .
oszacujmy szybkość zmiany amplitudy fali:
Rozpatrując energię przekazywaną do fali w jednostce czasu przez elektrony
grupy 1 i straty energii fali wywołane przez elektrony grupy 2 można znaleźć:
d 2e 2  2 df 0e

E0
2
dt me k
dv
v

vf 
k

k
ENERGIA FALI (na jednostkę objętości):
me ve2
1 2

E n
8
2
Stąd:

1 d

2 dt
1 2
E
4
E  Eo sin( kx  t )
4e 2 df 0e
me k 2 dv
v

k
DWA SŁOWA O POLU ELEKTROMAGNETYCZNYM (POPRZECZNYM) W PLAZMIE
Dla plazmy w polu o dużej częstości:
 p2
  1 2  1

W plazmie nie mogą rozchodzić się
fale o częstości mniejszej od  p
vf 

k

c

1

2
p
2
c
 (k )  c 2 k 2   p2
DLA FAL ELEKTROMAGNETYCZNYCH ROZCHODZĄCYCH SIĘ W PLAZMIE (BEZ
POLA MAGNETYCZNEGO) NIE WYSTĘPUJE TŁUMIENIE LANDAUA! – bo skoro v f  c
,to nie ma cząstek, które mogłyby być w rezonansie z tymi falami.
Jedynym mechanizmem tłumienia są kolizje (zderzenia cząstek).
Można je jawnie wprowadzić do przenikalności elektrycznej:
 p2
  1
   ivei 
   R  i I
RÓWNANIA KINETYCZNE
f ( x, y , z , v x , v y , v z , t )
np.
jednowymiarowo:
ile cząstek na jednostkę objętości w przestrzeni fazowej
f ( x, v, t ) 
l.czastek
dx  dv
v0
Jeśli zaniedbany zderzenia cząstek:
df f
f d v f

v 
0
dt t
 r dt v
gdzie:
RÓWNANIE WŁASOWA
(bezzderzeniowe równanie Boltzmanna)
d v qE

dt
m
  E  4  4e( f i d v   f e d v)
E
Kiedy można korzystać z równania
Własowa? Tzn. kiedy można zaniedbać
zderzenia cząstek?
x0
t 
- pole samouzgodnione

-średni czas swobodnego
przebiegu cząstki
Jeżeli zderzeń cząstek nie można pominąć to:
df
 St  f 
dt
całka zderzeń
dv
dx
W największym uproszczeniu
przyjmuje się często:
St f  
f0  f

  ( f o f )
operator Krooka (  -przybliżenie)
CAŁKA ZDERZEŃ – ciut dokładniej
Landau podał całkę zderzeń w pewnej „dyfuzyjnej” formie (przypominającej
dyfuzję Fokkera – Plancka) uwzględniając rozpraszanie cząstek tylko na bardzo
małe kąty.
JESZCZE BARDZIEJ UPROSZCZAJĄC SPRAWĘ MOŻNA OGRANICZYĆ SIĘ DO
DWÓCH EFEKTÓW:
1) Pojawienie się siły tarcia dynamicznego: FT  mv
(
dv
 iv ,
dt
co daje:
v
f)
 (vf )
t

v
v
2) Dyfuzyjnego błądzenia prędkości rozproszonej cząstki:
 ( D (v )
v
f
)
v
z pewnym współczynnikiem
dyfuzji w przestrzeni prędkości D (v)
D(v)  v 2
w rezultacie:

f
St f   (vf  D(v) )
v
v
W WIELU ZAGADNIENIACH FIZYKI PLAZMY (OSCYLACJE,
FALE) ZNAJOMOŚĆ CAŁKI ZDERZEŃ NIE JEST KONIECZNA BO
WYSTARCZY ROZPATRYWAĆ ZACHOWANIE PLAZMY W
CZASACH KRÓTSZYCH OD CZASU SWOBODNEGO PRZEBIEGU.
KINETYCZNE PODEJŚCIE DO FAL W PLAZMIE
~
   ei ( kx t )
poprawka do równania Własowa z
uwzględnieniem tylko wyrazów I-go rzędu
(linearyzacja)
f e  f (v)  f e ( x, v, t )
e
o
f e
f e e  f 0e
v

0
t
x me x v
można otrzymać równanie
dyspersyjne
f 0e
dv

4e 2 v
k 
me    kv
część urojona
część rzeczywista
Kontynuując rachunki
można wyliczyć
dekrement tłumienia:
f
2 e
 (
)
2
me k
v
2 2
P  ...dv
e
0
v

k
dla v 
+
f 0e
v
v

k
biegun
człon odpowiedzialny
za tłumienie
LANDAUA

k
Osobliwością tłumienia LANDAUA jest fakt, że entropia jest
zachowana! (bezzderzeniowe równanie!) A ZATEM
TŁUMIENIE POWINNO BYĆ ODWRACALNE!
TŁUMIENIE LANDAUA – drugie podejście


Rozważaliśmy cząstki grupy 1 – szybsze niż k i grupy 2 – wolniejsze od k .
W maxwellowskiej plazmie cząstek grupy 2 jest więcej dlatego fala zanika
ALE: (!)
po zderzeniu ze ściankami studni obie grupy cząstek zamieniają się rolami!
Dlatego „tłumienie” zmienia znak i okazuje się funkcją oscylującą o okresie oscylacji:
1
ściślej mówiąc byłoby tak, gdyby WSZYSTKIE
b
cząstki poruszałyby się synchronicznie
k e
m
W RZECZYWISTOŚCI OKRES OSCYLACJI ZALEŻY OD ENERGII (PRĘDKOŚCI) CZĄSTEK

v
1
k v 
k
x
mieszanie w przestrzeni prędkości
WCZEŚNIEJ CZY PÓŹNIEJ DOCHODZI
RÓWNIEŻ DO DYFUZJI W PRZESTRZENI
PRĘDKOŚCI
I
ZDERZENIA
CZYNIĄ
PROCES NIEODWRACALNYM
NIESTABILNOŚĆ TYPU WIĄZKI (bump on tail)
FALA NARASTA Z FLUKTUACJI TERMICZNEJ
AUTOMODULACJA WIĄZKI
vf
bliskie prędkości wiązki u0
NIESTABILNOŚĆ MOŻE POWSTAĆ TYLKO DLA
FAL SPELNIAJĄCYCH WARUNEK
  ku0
Wiązka rozbija się na „zgęstki” ściąganych w kierunku
hamujących faz pola i amplituda fali rośnie. Wzrost trwa, aż
zgęstki okażą się złapanymi cząstkami w „studniach” fali, wtedy
następuje już opisany proces oscylacji i stabilizacja amplitudy.
Cząstki muszą
gromadzić się w
obszarze hamujących
faz pola, a to wtedy

gdy:
uo 
k
uo 

jeśli by
k , to cząstki
gromadzą się w obszarze
przyśpieszających faz pola i
taka fala zaniknie (samoistnie
nie powstanie)