plik

Podsumowanie W4
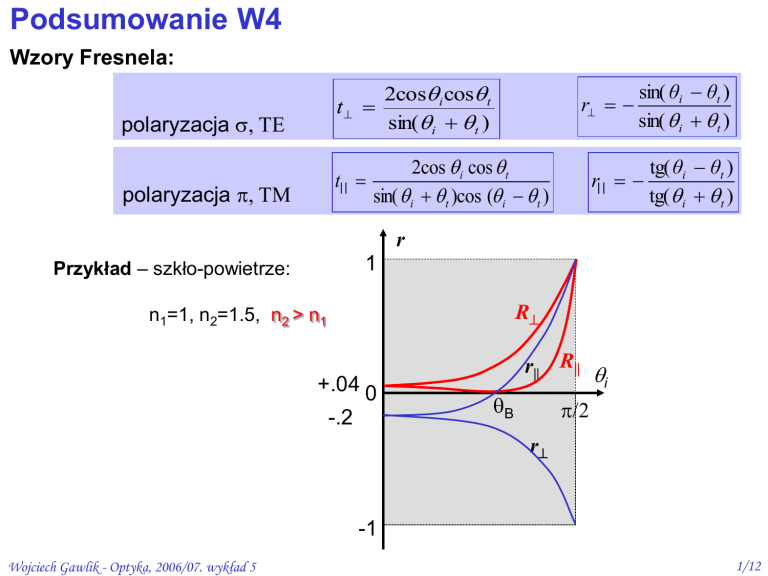
Wzory Fresnela:
t 
polaryzacja , TE
t|| 
polaryzacja , TM
2cos i cos t
sin( i   t )
r  
2cos  i cos  t
sin(  i   t )cos ( i   t )
sin( θi  θt )
sin(  i   t )
r||  
tg( θi  θt )
tg( i   t )
r
1
Przykład – szkło-powietrze:
R
n1=1, n2=1.5, n2 > n1
+.04 0
-.2
r|| R|| 
i
B
/2
r
-1
Wojciech Gawlik - Optyka, 2006/07. wykład 5
1/12
Znikanie r|| (@ B) to konsekwencja poprzeczności
fal EM i ich oddziaływania z materią
B
90o
• fala odbita to wynik
promieniowania całej
objętości ośrodka
• przy polaryzacji p,
r|| (i =B)=0,
• może się odbijać
tylko fala o polaryzacji s
Wojciech Gawlik - Optyka, 2006/07. wykład 5
2/12
Granica n1>n2
Gdy 2 =  /2, 1  graniczny
z
z
sin 1 n2

sin  2 n1
1
n1
n2
y
1
y
x
x
90o
2
a co gdy 1 > graniczny ? ?
sin  gr
1
?

n2
n1
n2
 gr  arcsin
n1
(dla granicy powietrze/szkło, gr = 42o)
n2
sin  2  n12sin  2
- prawo Snella: n1sin 1 = n2 sin 2
n1
 n2
- w przedziale 0-90o, sin1 , gdy 1 , czyli
 n sin  2
1
sin( 1   gr )  
n

n
 2
sin 1 
sin  2  1  C
1
n2
1
 n1
sin
2
C
możliwe w.t.w., gdy kąt 2 zespolony a cos2 urojony
2
n 
cos 2 2  1  sin 2 2  1   1  sin 21  0
 n2 
Wojciech Gawlik - Optyka, 2006/07. wykład 5
2
n 
cos 2  i  1  sin 21  1  im
 n2 
(tylko „-” ma sens fizyczny)
3/12
Współczynnik odbicia dla n1>n2
r  
sin( θ1  θ2 )
sin θ1cos θ2  sin θ2cos θ1
sin θ2cos θ1  im sin θ1
z


 *
sin( 1   2 )
sin θ1cos θ2  sin θ2cos θ1
sin θ2cos θ1  im sin θ1
z

podobnie dla r|| więc |R ,|||2 = rr* 1
całkowite odbicie !
(wewnętrzne)
r
1
R
R||
0
Wojciech Gawlik - Optyka, 2006/07. wykład 5
B
gr
i
/2
4/12
Pole po drugiej stronie?
cos 2  im
Et  t E0e
 
ik  r
 t E0 e
 
k  r  k x cos(k , x)  z cos(k , z )
ik ( x sin 2  z cos 2 )
 t E0 e
i k ( 1 m 2 ) x
e k m z
z
1
 k x sin  2  z cos  2 
fala propagująca wzdłuż x
y
2
exp. zanik w kier. z
x
To nie jest fala płaska !
Fala zanikająca:
E(z)
z
 gr
y

x
z
Wojciech Gawlik - Optyka, 2006/07. wykład 5
5/12
Fala zanikająca
d >> 
d
d << 
- zastosowanie: regulowane rozdzielacze wiązek świetlnych
- Dośw.
Wojciech Gawlik - Optyka, 2006/07. wykład 5
6/12
Miraże
Wojciech Gawlik - Optyka, 2006/07. wykład 5
n1>n2
7/12
Daleki odbiór fal radiowych – odbicie od jonosfery
e 2 N el
n   0   1 
2 0 m  2
Wojciech Gawlik - Optyka, 2006/07. wykład 5
- silna zależność od
aktywności Słońca
-  częstość graniczna
8/12
Mikroskopia bliskiego pola
Wojciech Gawlik - Optyka, 2006/07. wykład 5
9/12
Światłowody
- wykorzystują całkowite odbicie
- problemy
a) wprowadzenie i wyprowadzenie wiązki
b) fala zanikająca (specjalne konstrukcje, płaszcz)
c) absorpcję – specjalne materiały (kwarc) i odpowiednia dł. fali
d) zginanie – minimalny kąt zgięcia
e) zniekształcenia krótkich impulsów
Wojciech Gawlik - Optyka, 2006/07. wykład 5
10/12
Odbicie od metali
• duża koncentracja swobodnych elektronów
 silna absorpcja, silne oscylacje swobodnych elektronów
oscylacje swob. elektronów  z „częstością plazmową”
ne 2
 
  p2
 L 0 m
2
 propagacja w głąb metalu silnie osłabiana,
 różnica faz między polami E i B
(inaczej niż w dielektrykach)
 zespolona stała dielektryczna i
E  E0 e
 
i ( k r  t )
Wojciech Gawlik - Optyka, 2006/07. wykład 5

  n  i z dużym 
 
k  n  k   
c
c
2
2
11/12
   p 2 
   L 1    
    
 
k   
c
2
2

1) dla  > p ,  jest dodatnie a k rzeczywiste,
R
Ir

I0
 1
 1
2
/p
 współcz. odbicia
0.8 1
1
R
2) dla  < p , k jest urojone, brak propagującej
fali sinusoidalnej, ampl. zanika wykładniczo
i cała energia jest w fali odbitej
.5
/p
(kompensacja prądów związanych
z L i z oscylacjami elektronów)
3) dla  ;  =1, tzn.
   min   p
2
0
0.8 1
L
11
1
 L 1
(minimum plazmowe) brak odbicia, R=0
2
Al
R
Ag
Au
1
.50.5
„metaliczny” odblask i kolory metali
0 00
0
0
0
Wojciech Gawlik - Optyka, 2006/07. wykład 5
1
1
2
2
3
y
3
4
4
5
55
ħ [eV] 12/12