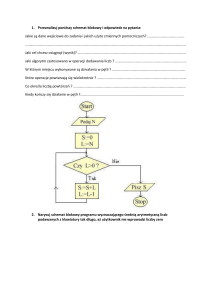
Przykłady zadań zamkniętych i otwartych z kombinatoryki
W nawiasach podano punktację za zadania otwarte, tak jak w zadaniach maturalnych.
Zadania zamknięte
Zadanie 1
pewnym regionie wyboru imion nowonarodzonym dzieciom można dokonać z wykazu zawierającego
100 imion. Nadając dziecku dwa imiona można to zrobić na:
A. 100 sposobów B. 99 sposobów
C. 100x100 sposobów D. 100x99 sposobów
Zadanie 2
Rzucamy równocześnie kostką sześcienną i monetą symetryczną. Liczba wszystkich wyników rzutu wynosi:
A. 2
B. 4
C. 6
D. 12
Zadanie 3
W kwadracie przedstawionym na rysunku należy pomalować dwa z czterech pól
oznaczonych cyframi od 1 do 4. Różnych sposobów wykonania tego zadania jest: 1 2
A. 4
B. 5
C. 6
D. 3
3 4
Zadanie 4
W pudełku znajdują się 2 kule czerwone (c) i 1 zielona (z). Z pudełka losujemy po jednej kuli tak długo,
aż zostanie wylosowana ostatnia kula i będzie to kula zielona. Graf, który ilustruje wyniki tego losowania
to:
a)
b)
c)
d)
z
z
c
c
c
c
z
z
z
z
c
c
c
c
c
z
z
z
Zadania otwarte
We wszystkich zadaniach otwartych należy uzasadnić rozwiązanie.
Zadanie 1 (2 pkt.)
Numer dowodu osobistego składa się z 9 znaków. Trzy pierwsze to litery wybrane spośród 25 liter,
a pozostałe znaki to cyfry. Ile różnych numerów dowodów osobistych można przydzielić obywatelom?
Zadanie 2 (2 pkt.)
Oblicz ile różnych liczb trzycyfrowych można utworzyć z podanych cyfr (cyfry nie mogą się powtórzyć):
1,3,6,8.
Zadanie 3 (2 pkt.)
W klasie jest 17 dziewcząt i 12 chłopców. Wybieramy losowo 5 osobową delegacje. Ile różnych delegacji
można utworzyć?
Zadanie 4 (4 pkt.)
W zestawie zadań jest 15 zadań łatwych i 5 zadań trudnych.
a) Na ile sposobów można z tego zestawu wybrać 3 zadania?
b) Na ile sposobów można z tego zestawu wybrać 3 zadania, tak, aby 2 były łatwe i 1 trudne?
Zadanie 5 (5 pkt.)
Na przyjęcie przyszła pewna liczba osób, przy czym każdy przywitał się z każdym. Ile było osób na
przyjęciu, jeśli nastąpiło 15 powitań?
Zadanie 6 (6 pkt.)
Ze zbioru 0,1,3,5,6,7,8 losujemy kolejno bez zwracania trzy liczby, a następnie układamy je w kolejności losowania w liczbę trzycyfrową. Ile można w ten sposób utworzyć:
a) dowolnych liczb,
b) liczb nieparzystych,
c) liczb mniejszych niż 538?
Przygotowała: Iwona Głowacka