Cząsteczki

Cząsteczki
1.
2.
3.
4.
Kwantowy opis stanów energetycznych cząsteczki
Funkcje falowe i energia elektronów
Ruchy jąder (oscylacje i rotacje)
Wzbudzenia cząsteczek
Opis kwantowy cząsteczki jest bardziej skomplikowany niż atomu.
Hamiltonian przy zaniedbaniu oddziaływań związanych ze spinem ma
następującą postać:
2
2
2
Z
e
h
h
1
2
2
N
Hˆ = −
∇
−
∇
−
∑
∑
∑
i
N
r r
2m i
4πε 0 N ,i ri − RN
N 2M N
+
1
4πε 0
∑
N <K
Z N Z K e2
1
r
r +
RN − RK 4πε 0
∑
i< j
e2
r r
ri − rj
gdzie jądra oznaczone są symbolami N lub K, elektrony zaś i lub j;
m, e – odpowiednio masa i ładunek elektronu;
MN, Z
Ne - odpowiednio masa i ładunek N-tego jądra;
r
r
r R oznaczają współrzędne elektronów i jąder.
i
N
r r
r R
r
r
r
r
r
r
Hˆ (r , R )Ψ (r , R ) = EΨ (r , R )
symbolizują skrótowo wszystkie współrzędne elektronów i jąder
Problem upraszcza się znacznie, kiedy wiedząc że jądra atomowe są znacznie cięższe
od elektronów i poruszają się znacznie wolniej od nich wyeliminujemy z
hamiltonianu energię kinetyczną jąder (przybliżenie M=∞). Powstałe w ten sposób
nowe r. Schrodingera opisuje ruch tylko elektronów przy ustalonej konfiguracji jąder.
r k r r
r
r
r
k
k
Hˆ el (r , R )ψ el (r , R ) = Eelψ el (r , R )
Okazuje się, że trzymając się dalej tego przybliżenia, można
całą funkcję falową
r
n
zapisać w postaci iloczynu
funkcji
falowej
jądrowej
χ
(R) i funkcji falowej
r
n r
elektronowej ψ el (r , R) , przy ustalonym położeniu jąder.
r n r r
r r
n
Ψ (r , R) = χ ( R)ψ el (r , R)
Funkcja opisująca ruch jąder spełnia następujące równanie:
r
r
r
[TˆN + Eeln ( R)]χ n ( R) = Eχ n ( R)
gdzie T̂N jest operatorem energii kinetycznej jąder, zaś
elektronów przy ustalonym położeniu jąder.
r
E (R)
n
el
jest energią
Ruch jąder odbywa się w potencjale wyznaczonym przez
energię n-tego stanu
r
elektronowego i często mówi się, że zależność Eeln (R) wyznacza powierzchnię
energii potencjalnej.
Opisane postępowanie nosi nazwę przybliżenia Borna-Oppenheimera.
Operator TˆN zawiera część odpowiadającą ruchowi postępowemu środka masy
cząsteczki – pominiemy ją, nie jest skwantowana i istotna dla nas.
W operatorze tym mamy jeszcze składnik odpowiadający energii kinetycznej
drgań (oscylacji) jąder wokół położeń równowagi Tˆ
oraz obrotu (rotacji) cząsteczki jako całości
Tˆrot
osc
.
Dla małych drgań (zaniedbujemy zmianę odległości jąder i modyfikację momentu
bezwładności, wpływające na obrót cząsteczki) i powolnych obrotów
(zaniedbujemy siłę odśrodkową, zmieniającą położenie równowagi jąder) można
rozseparować ruch oscylacyjny i rotacyjny oraz zapisać jądrową część funkcji
falowej jako:
r
r
r
χ ( R) = χ osc ( R) χ rot ( R)
Wracając do całkowitej funkcji falowej i całkowitej energii mamy zatem:
r
r
r
r r
n r
Ψ (r , R) = ψ el (r , R) χ osc ( R) χ rot ( R)
E = E el + E osc + E rot
Szukamy
r więc najpierw energii elektronowej sparametryzowanej przez położenie
jąder R , a następnie rozważamy ruch oscylacyjny i rotacyjny jąder.
Rozważmy najprostszą cząsteczkę H2+.
Hamiltonian dla funkcji elektronowej ma postać:
2
2
2
e
e
h
Hˆ el = −
Δ−
−
2me
4πε 0 r1 4πε 0 r2
Gdzie
r1 i r2 są odległościami elektronu od odpowiednio pierwszego i drugiego jądra.
kombinacja
symetryczna
orbital wiążący
kombinacja
antysymetryczna
orbital antywiążacy
Budowanie elektronowej funkcji falowej cząsteczki H2+
Cząsteczka H2+
Ψ+ = N + (1s A + 1sB )
Ψ− = N − (1s A − 1sB )
⎡1 2
⎤
2
⎢⎣ 2 (ϕ A + ϕ B ) + ϕ Aϕ B ⎥⎦
1 ⎡1 2
⎤
2
2
Ψ− =
(ϕ A + ϕ B ) − ϕ Aϕ B ⎥
⎢
1− S ⎣ 2
⎦
1
Ψ =
1+ S
2
+
Cząsteczka H2+
Odległość jąder atomowych
dla minimum energii, Re
Re=130 pm
Re=106 pm doświadczenie
Energia dysocjacji, De
De=1.77 eV,
doświadczenie
De=2.6 eV
Eel
Energie elektronowe odpowiadające stanom
wiążącym i antywiążacym w cząsteczce H2+.
R oznacza tu odległość między jądrami
Cząsteczka wodoru H2
r r
r
r
r
r
1
ΨS (r1 , r2 ) =
[ S (r1 A ) ⋅ S (r2 B ) + S (r1 B ) ⋅ S (r2 A )]
2
r r
r
r
r
r
1
ΨA (r1 , r2 ) =
[ S (r1 A ) ⋅ S (r2 B ) − S (r1 B ) ⋅ S (r2 A )]
2
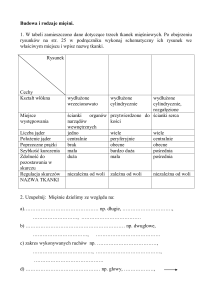
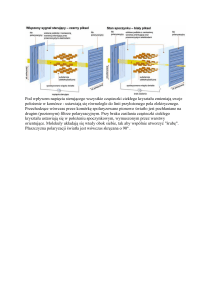
Ze względu na zakaz Pauliego funkcja falowa dwóch
identycznych elektronów musi być antysymetryczna. Oznacza to,
że dla elektronów o przeciwnych spinach część przestrzenna
funkcji falowej musi być symetryczna, zaś dla elektronów o
takich samych spinach – część przestrzenna funkcji falowej musi
być antysymetryczna. To gwarantuje, że cała funkcja jest
antysymetryczna. U góry pokazane jest to dla dwóch atomów
wodoru w dużej odległości. Po lewej stronie funkcje falowe dla
dwóch atomów w cząsteczce. Widać tworzenie się stanu
wiążącego i antywiążacego.
Cząsteczka wodoru H2
Oddziaływanie między elektronami
prowadzi do silnego wiązania
cząsteczki wodoru, energia
dysocjacji wynosi 4.52 eV, zaś
odległość między jądrami 0,74Å.
Na rysunku widać energie elektronową dla stanu wiążącego (z
minimum) i stanu antywiążacego.
orbitale σ - nie ulegają zmianie przy obrotach
wokół osi cząsteczki
orbitale π - zmieniają znak przy obrocie o π.
g – gerade parzyste przy inwersji względem
środka cząsteczki
u – ungerade nieparzyste.
Liczba na początku – numer porządkowy
orbitalu danego typu.
Oscylacje i rotacje cząsteczek
Postać równania Schrodingera dla ruchu jąder
r n r
r
n
[TˆN + E ( R)]χ ( R) = Eχ ( R)
n
el
Rozważamy molekułę dwuatomową:
W przypadku molekuły dwuatomowej wygodnierjest przejść do współrzędnej opisującej
odległość między atomami. Oznaczymy ją też R
r
Powyższe równanie oznacza więc możliwość zmiany długości wektora R , czyli
oscylacje oraz zmianę jego orientacji w przestrzeni, czyli rotacje cząsteczki.
Rozwiązanie prowadzi nas do rotacyjnej części funkcji falowej, opisanej przez
harmoniki sferyczne
r
χ rot ( R) = χ rot (θ , ϕ ) = YJM (θ , ϕ )
J
E rot
h 2 J ( J + 1) h 2 J ( J + 1)
=
=
= BJ ( J + 1)
2
2I
2μRe
Rotacyjna liczba kwantowa J wyznacza moment pędu cząsteczki, a liczba
kwantowa M=-J,…+J jego rzut na wyróżniony kierunek w przestrzeni.
I jest momentem bezwładności jąder względem osi przechodzącej przez środek
masy i prostopadłej do osi cząsteczki, zaś B nosi nazwę stałej rotacji.
Re jest odległością jąder odpowiadającą stanowi równowagi ze względu na
drgania.
Odległości między kolejnymi poziomami rotacyjnymi wynoszą więc:
J
J −1
Erot
− Erot
= 2 BJ
Przejścia rotacyjne
Dozwolone są przejścia dla ΔJ = ±1
Obserwujemy równoodlegle linie
Widma rotacyjne
⎛ E ⎞
N ∝ g rot exp⎜⎜ − rot ⎟⎟
⎝ k0T ⎠
⎛ BJ ( J + 1) ⎞
⎟⎟
N J ∝ (2 J + 1) exp⎜⎜ −
k0T ⎠
⎝
Dla części oscylacyjnej, w przybliżeniu małych drgań mamy:
r
v
χ ( R) = χ osc
( R) = N v exp(− x 2 / 2) H v ( R)
v
osc
Ev = hω (v + 1 / 2)
Dozwolone przejścia optyczne
Δv=1
wielomian
Hermite’a
Parametry oscylacji
Parametr rotacji
cząsteczka
v (1013Hz)
Energia (meV)
C2
4,92
204
cząsteczka
B(meV)
N2
7,07
293
OH
2,341
O2
4,37
196
HCl
1,32
HCl
8,64
357
NO
0,211
HBr
7,65
316
CO
0,239
HJ
11,88
491
KBr
0,01
Odległości energetyczne poziomów oscylacyjnych są większe niż
poziomów rotacyjnych.
Stany oscylacyjno-rotacyjne
Gałąź R
ΔJ = J’ – J’’ = +1
Gałąź P
ΔJ = J’ – J’’ = -1
Widmo oscylacyjno-rotacyjne
Widma rotacyjne związane są tylko ze zmianą ruchu obrotowego – λ~ 0.1 – 10 cm
(mikrofale)
Widma oscylacyjno-rotacyjne odpowiadają jednocześnie zmianie stanu drgań i rotacji
cząsteczki – λ ~ 1 – 100 μm (podczerwień)
Widma elektronowo-oscylacyjno-rotacyjne związane są ze zmianą stanu chmury
elektronowej, której towarzyszy też zmiana oscylacji i rotacji – λ ~ 100 nm – 1 μm
(zakres widzialny i nadfioletu)
⎛
1⎞
E = E + BJ ( J + 1) + hωe ⎜ ν + ⎟
⎝
2⎠
n
el
Prawa przejść optycznych
Gdy następuje zmiana stanu energetycznego układu o ΔE, może być
wyemitowana lub zaabsorbowana energia ΔE w postaci fotonu
promieniowania elektromagnetycznego.
Nie wszystkie możliwe przejścia są dozwolone.
Rozważmy najprostszy układ - atom dwupoziomowy i jego
oddziaływanie z polem promieniowania,
zapiszemy jako
rktóre
r
r
zaburzenie w postaci fali płaskiej E cos( k r − ωt )
r
rr
rr
⎛ h2
⎞ r
∂ψ (r , t )
⎜⎜ −
Δ + V + eEr cos(k r − ωt ) ⎟⎟ψ (r , t ) = ih
∂t
⎝ 2me
⎠
r
r =0
Niech atom znajduje się w
Długość fali promieniowania elektromagnetycznego jest typowo
znacznie większa niż zasięg funkcji
elektronowych w atomie, więc
r
przyjmiemy w fali płaskiej r = 0
W takim przypadku hamiltonian ma postać
r
rr
⎛ h2
⎞ r
∂ψ (r , t )
⎜⎜ −
Δ + V + eEr cos ωt ⎟⎟ψ (r , t ) = ih
∂t
⎝ 2me
⎠
Hamiltonian bez zaburzenia ma postać
r
⎛ h
⎞ r
∂ψ (r , t )
⎜⎜ −
Δ + V + ⎟⎟ψ (r , t ) = ih
∂t
⎝ 2me
⎠
2
i jego rozwiązaniem są funkcje własne atomu. Jako zaburzenie
pojawiać się będą wyrażenia typu:
rr
r 3
* r
H ij = ∫ψ i ( r )eEr ψ j ( r ) d r
Wyrażenia takie nazywamy elementami macierzowymi
momentu dipolowego przejścia. Znikanie tych elementów
oznacza brak zmiany funkcji falowej, czyli oznacza, że nie ma
przejścia między poziomami atomu.
Widać, że zawsze Hii=0.
Jeśli światło spolaryzowane np. w kierunku z (w kierunku z drga
wektor natężenia pola elektrycznego), to element macierzowy
momentu dipolowego przejścia ma postać
r
r 3
H ij = ∫ψ ( r )eEzψ j ( r ) d r
*
i
Zbadamy ten element między funkcjami własnymi atomu wodoru
H ij = ∫ψ n*,l ,m ( r ,θ , ϕ )eEr cos θψ n ',l ',m ' ( r ,θ , ϕ ) d 3r
ψ n*,l ,m (r ,θ , ϕ ) = ψ n,l (r ,θ )e −imϕ
ψ n ',l ',m ' (r ,θ , ϕ ) = ψ n ',l ' (r ,θ )eim 'ϕ
H ij ≠ 0
dla m=m’
Można też pokazać, że dla światła spolaryzowanego w kierunku x lub y
element macierzowy nie znika jeśli m = m'±1
Reguła wyboru dla momentu pędu elektronu l = l '± 1
może też być otrzymana w podobnych, ale nieco bardziej żmudnych
rachunkach.
Opierając się na ścisłej teorii oddziaływań między światłem i
elektronami oprócz przejść dipolowych elektrycznych dostajemy także
przejścia wyższych rzędów:
- magnetyczne dipolowe
-elektryczne kwadrupolowe
-magnetyczne kwadrupolowe
-elektryczne oktupolowe itd.