22. Iloczyn skalarny, baza ortogonalna, baza ortonormalna, iloczyn

Monika Włodarczyk,Martyna Szczecioska
22. Iloczyn skalarny, baza ortogonalna, baza ortonormalna,
iloczyn wektorowy, przekształcenia izometryczne.
Iloczyn skalarny
Do przykładu 2) g1,…,gn
R
Monika Włodarczyk,Martyna Szczecioska
Baza ortogonalna i ortonormalna
Definicja . W przestrzeni liniowej z iloczynem skalarnym < , > wektory u,v
są ortogonalne (lub prostopadłe) gdy <u,v>=0. Piszemy wtedy u v.
V
Wynika to ze wzoru na iloczyn skalarny w ,który jest postaci
=
cos(u,v). Jeżeli u i v są prostopadłe to kąt między nimi wynosi
,ponieważ cos = 0 to
=0.
Definicja . Podprzestrzenie liniowe
skalarnym są ortogonalne,gdy
.
i
,przestrzeni liniowej V z iloczynem
dla
,
. Piszemy wtedy
Dopełnieniem ortogonalnym podprzestrzeni liniowej U przestrzeni liniowej
nazywamy podprzestrzeo liniową
={ v
V;
}
Definicja . Mówimy, że układ wektorów
z przestrzeni V jest układem
ortogonalnym gdy <
,
> = 0 dla j k . Układ jest ortonormalny gdy jest
ortogonalny oraz <
,
> = 1 dla
.
Układ wektorów jest bazą ortogonalną (odpowiednio bazą ortonormalną
)przestrzeni liniowej z iloczynem skalarnym , gdy jest jej bazą oraz układem
ortogonalnym (odpowiednio ortonormalnym ).
Przykład.
1. Baza kanoniczna (
) jest bazą ortonormalną przestrzeni
ze
standardowym iloczynem skalarnym.
2. Przy iloczynie
,
,w
baza kanoniczna jest bazą
ortogonalną, a bazą ortonormalną jest np.(
).
3. W przestrzeni rodzina ciągów , w której ciąg i-ty ma na i-tym miejscu 1
a na pozostałych 0, stanowi układ ortonormalny w tej przestrzeni.
Monika Włodarczyk,Martyna Szczecioska
Stwierdzenie (Ortogonalizacja Schmidta)
Niech (
) będzie liniowo niezależnym układem wektorów w
przestrzeni liniowej V z iloczynem skalarnym < , >. Układ wektorów
(
) określony warunkami :
–
dla j= 2,…,k
stanowi bazę ortogonalną podprzestrzni liniowej lin(
Ponadto układ (
).
) jest bazą ortonormalną
podprzestrzeni lin (
).
Wniosek.
Każda przestrzeo liniowa posiada bazę ortonormalną .
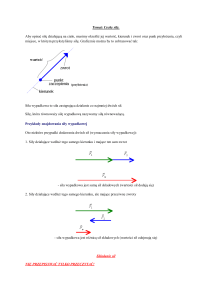
Iloczyn wektorowy
Iloczynem wektorowym wektorów a=*
] i b= [
nazywamy wektor, który ma następujące współrzędne :
[
I oznaczamy go przez
]
]
.
Sposób obliczania iloczynu wektorowego:
Iloczyn wektorowy wektorów a=*
przez wyznacznik :
=
] i b= [
+ można wyrazid
Monika Włodarczyk,Martyna Szczecioska
gdzie i,j,k są wersorami osi . Wyznacznik ten formalnie nie ma sensu
(pierwszy wiersz składa się z wektorów) ale pozwala łatwo zapamiętad
sposób obliczania iloczynu wektorowego .
Można zauważyd,że:
(i)
(ii)
(iii)
|
= |a||b|
,
Wektor
jest ortogonalny do wektora a i b ,
Zwrot wektora
jest określony przez regułę śruby prawoskrętnej
lub trzech palców lewej dłoni .
Konstrukcja wektora
Przykład
Monika Włodarczyk,Martyna Szczecioska
Przekształcenia Izometryczne
Przykłady :
(1) Symetria
(2) Obrót
(3) Przesunięcie o wektor
Monika Włodarczyk,Martyna Szczecioska
Przekształcenie które nie jest izometrią:
- rzut prostopadły (zmienia odległosd)
-jednokładnośd