PRZYGOTOWANIE DO SPRAWDZIANU

PRZYGOTOWANIE DO SPRAWDZIANU - FUNKCJA LINIOWA - POZIOM
ROZSZERZONY 2013_2014.doc
(362 KB) Pobierz
PRZYGOTOWANIE DO SPRAWDZIANU FUNKCJA LINIOWA - POZIOM ROZSZERZONY
DOPUSZCZAJĄCY
1. Motocyklista jadący ze stałą prędkością w ciągu 4 sekund przejeżdża 32 metry.
Ile km przejedzie kolarz w ciągu 1,5 godziny, jadąc z tą samą prędkością.
2. Sprawdź algebraicznie, czy do wykresu funkcji liniowej
a)
należy punkt :
b)
należy do wykresu funkcji liniowej
3. Punkt
. Wyznacz b.
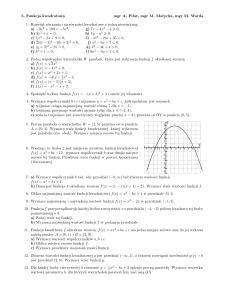
4. Na podstawie wykresu funkcji liniowej f :
a) wyznacz współczynnik kierunkowy tej funkcji
b) określ monotoniczność funkcji
c) Podaj współrzędne punktu przecięcia wykresu z osią OX
5. a) Oblicz miejsce zerowe funkcji liniowej
b) Dla jakich argumentów funkcja liniowa
.
przyjmuje wartości dodatnie ?
6. Napisz wzór oraz naszkicuj wykres funkcji liniowej :
a)
b)
do której wykresu należą punkty
i
wiedząc, że miejscem zerowym jest liczba 3 oraz
7. Wyznacz kąt nachylenia wykresu funkcji liniowej
do osi OX.
8. Wyznacz m,
dla którego wykresy funkcji liniowych
a) równoległe
są :
oraz
b) prostopadłe
9. Napisz wzór funkcji liniowej, której wykres jest :
a)
równoległy do wykresu funkcji
i przechodzi przez punkt
;
b)
prostopadły do wykresu funkcji
i przechodzi przez punkt
.
10. W korporacji taksówkowej obowiązuje następujący system opłaty za przejazd
: za pierwszy
kilometr 6,30 zł, a za każdy następny (rozpoczęty) kilometr 1,80 zł. Podaj wzór funkcji f
opisującej wysokość opłaty za przejazd w zależności od liczby n przejechanych kilometr
ów.
11. Rozwiąż równanie i nierówność :
a)
b)
12. Rozwiąż układ równań
metodą podstawiania lub przeciwnych współczynn
ików.
13. Podaj interpretację graficzną nierówności
w układzie współrzędnych.
14. Suma dwóch liczb jest równa 35. Jeżeli jedną z nich potroić, a drugą pomnożyć przez 4
to otrzymamy w sumie 125. Znajdź te liczby.
DOSTATECZNY
1. Wyznacz wzór funkcji liniowej
w punkcie
, wiedząc, że jej wykres przecina oś OY
oraz
.
2. Napisz wzór funkcji liniowej wiedząc, że :
a) jej wykres przechodzi przez punkt
b)
i
i jest nachylony do osi OX pod kątem
.
oraz narysuj wykres tej funkcji.
3. Dla jakich wartości parametru m, funkcja liniowa
nieskończenie wiele miejsc zerowych.
ma
4. Wyznacz wartości parametru k,
dla których prosta określona równaniem
przechodzi przez I, II i III ćwiartkę układu współrzędnych.
5. Dana jest funkcja liniowa f o wzorze
a) Dla jakich a funkcja f jest malejąca ?
.
b) Dla
wyznacz zbiór tych argumentów,
dla których wartości funkcji f należą do przedziału
.
6. Napisz wzór funkcji liniowej,
której wykres otrzymujemy w wyniku przesunięcia równoległego
wykresu funkcji
o wektor
.
7. Dla jakich wartości parametru k,
przecina oś OY
wykres funkcji liniowej
poniżej punktu
.
8. Dane są wzory funkcji liniowych : f(x) = 2x – 4, g(x) = x + 1, h(x) = ax – 7
Dla jakich a wykresy funkcji przecinają się w tym samym punkcie ?
9. Naszkicuj wykres funkcji f(x) =
a) Oblicz wartość funkcji f dla argumentu 6.
b) Oblicz miejsca zerowe funkcji f
.
10. a) Rozwiąż równanie
b) Rozwiąż nierówność
.
. Wypisz wszystkie liczby naturalne spełniające
tę nierówność.
11. Dane jest równanie z niewiadomą x.
Przedyskutuj liczbę i rodzaj rozwiązań równania
ze względu na wartość parametru m.
12. Dopisz brakujące równanie układu
tak, aby powstały układ równań był :
a) sprzeczny
b) nieoznaczony
c) oznaczony
13. Dany jest układ równań z niewiadomymi x i y :
.
a) Rozwiąż ten układ dla
i
metodą wyznacznikową.
b) Dobierz współczynniki a i b tak,
aby rozwiązaniem układu równań była para liczb
14. Rozwiąż układ równań
15. Podaj interpretację graficzną układu nierówności
.
.
w układzie współrzędnych.
16. Zilustruj zbiór wszystkich punktów płaszczyzny,
których współrzędne spełniają równanie
17. Pan Nowak ma sklep z owocami i warzywami.
W hurtowni kupił 80 kg jabłek oraz 20 kg
papryki czerwonej za łączną kwotę 328 zł. Do ceny hurtowej jabłek sklepikarz doliczył
20% marży, zaś do ceny hurtowej papryki doliczył 25% marży.
Wówczas za 5 kg jabłek i 2 kg
papryki trzeba było zapłacić w sklepie pana Nowaka 29 zł. Ile kosztuje
1 kg jabłek oraz 1 kg
papryki czerwonej w hurcie, a ile w detalu ?
DOBRY
1. Wyznacz te wartości parametru m :
a)
dla którego miejsce zerowe funkcji
jest liczbą nie mniejszą niż 4.
b) dla których wykresy funkcji f i g są równoległe,
gdy
oraz
.
c)
dla których funkcji f i g są prostopadłe, gdy
d)
dla których funkcja f dana wzorem
oraz
.
jest rosnąca i jednocze
śnie
wykres funkcji f przecina oś OY poniżej punktu
.
2. Napisz wzór funkcji liniowej f, której wykres przechodzi przez punkt A(–
nachylony
, –2) i jest
do osi OX pod takim kątem , że cos  =
. Podaj wzór proporcjonalności prostej, której
wykres jest prostopadły do wykresu funkcji f.
3. Dane są dwie funkcje liniowe
oraz
Wyznacz wartość parametru m,
dla którego zbiorem rozwiązań nierówności
4. Dane są dwie funkcje liniowe
jest przedział
.
. Wyznacz wartość
oraz
parametru m, dla którego zbiór rozwiązań nierówności
w przedziale
.
.
zawiera się
5. Rozwiąż układ nierówności :
6. Rozwiąż równanie : a)
metodą algebraiczną
metodą graficzną.
b)
7. Rozwiąż nierówność : a)
metodą algebraiczną
metodą graficzną.
b)
8. Dane jest równanie z niewiadomą x. Przedyskutuj liczbę i rodzaj rozwiązań równania
ze względu na wartość parametru k.
9. W zależności od wartości parametru a przeprowadź dyskusję istnienia i liczby rozwiązań
układu równań
.
10. Dla jakich wartości parametru m rozwiązaniem układu równań
a
liczb ujemnych ?
jest par
11. Opisz za pomocą układu nierówności :
a)
trójkąt o wierzchołkach
,
i
b) przedstawioną figurę geometryczną
...
.
Plik z chomika:
asia19962
Inne pliki z tego folderu:

PRZEWODNIK PO GRAMATYCE ANGIELSKIEJ - 2000 - Lucyna Gołębiowska.pdf
(35323 KB)
 Technical English 3 WorkBook.pdf (34904 KB)
 Matura Success Advanced Students Book.pdf (33849 KB)
 Technical English 2 Teacher'sBook.pdf (28611 KB)
 M. Matasek English Advanced Vocabulary and Structure Practice.pdf (9926 KB)
Inne foldery tego chomika:

Dokumenty
FILMY
Galeria
 MUZYKA
 Prywatne


Zgłoś jeśli naruszono regulamin







Strona główna
Aktualności
Kontakt
Dla Mediów
Dział Pomocy
Opinie
Program partnerski




Regulamin serwisu
Polityka prywatności
Ochrona praw autorskich
Platforma wydawców
Copyright © 2012 Chomikuj.pl