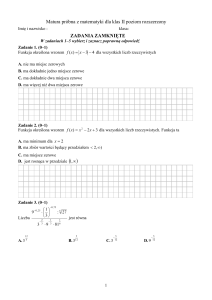
Zadanie 1. (5 p.)
Hurtownik sprzedaje grille żeliwne po 50 zł za sztukę, o ile zamówienie jest mniejsze niż 10
sztuk. Jeśli zamówienie jest niemniejsze niż 10 sztuk, ale nie większe niż 130 sztuk, to
wówczas cena jednego grilla spada o 0,2 zł pomnożone przez liczbę zamówionych sztuk.
a) Napisz wzór funkcji opisującej przychód hurtownika w zależności od liczby sprzedanych
sztuk.
b) Jaka wielkość zamówienia zmaksymalizuje przychód hurtownika? Ile wyniesie
maksymalny przychód?
Zadanie 3. (5 p.)
a) Wyznacz postać ogólną i iloczynową funkcji kwadratowej, o której wiadomo, że dla
argumentu 3 osiąga najmniejszą wartość równą (–8), a jednym z jej miejsc zerowych jest
liczba 5.
b) Dla jakich argumentów funkcja ta osiąga wartości nieujemne?
Zadanie 4. (5 p.)
Ułóż równanie kwadratowe takie, aby suma pierwiastków równania była równa 4, a suma
odwrotności pierwiastków wynosiła –5.
Zadanie 1. (5 p.)
Pierwiastkami równania x2 – 2px + p = 0 są dwie różne liczby x1, x2. Stosując wzory Viete’a
zbadaj, czy istnieje taka wartość parametru p, dla której (x1 + 5x2)(x2 + 5x1) osiąga wartość
13.
Zadanie 2. (6 p.)
Funkcja kwadratowa f określona jest wzorem f(x) = ax2 + bx + 1 dla xR.
a) Wyznacz wzór tej funkcji tak, aby f(–1) = –3 i f(4) = – 3.
b) Dla wyznaczonych współczynników a i b, wyznacz największą wartość funkcji w
przedziale domkniętym 1, 2.
c) Dla wyznaczonych współczynników a i b rozwiąż nierówność f(x) > 1.
Zadanie 3. (5 p.)
Rozwiąż nierówność:
3 2x x 2 x 1.
Zadanie 4. (4 p.)
Rozwiąż równanie: |x2 – 1| + |x + 1| = 0.
Zadanie 5. (4 p.)
Wykaż, że dla dowolnych liczb rzeczywistych a, b, c równanie x2 + (a + b)x + ab – c2 = 0
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Zadanie 6. (6 p.)
Dla jakich wartości parametru m (mR) równanie x2 – 2(m– 2)x + m2 – 2m – 3 = 0 ma dwa
różne pierwiastki rzeczywiste dodatnie?
Zadanie 1. (5 p.)
Pierwiastkami równania x2 + mx – m = 0 są dwie różne liczby x1, x2. Stosując wzory Viete’a
zbadaj, czy istnieje taka wartość parametru p, dla której (x1 + 3x2)(x2 + 3x1) osiąga wartość 4.
Zadanie 2. (6 p.)
Funkcja kwadratowa f określona jest wzorem f(x) = ax2 + bx + 1 dla xR.
a) Wyznacz wzór tej funkcji tak, aby f(1) = 6 i f(2) = 1.
b) Dla wyznaczonych współczynników a i b, wyznacz największą wartość funkcji w
przedziale domkniętym 1, 2.
c) Dla wyznaczonych współczynników a i b rozwiąż nierówność f(x) >1.
Zadanie 3. (5 p.)
Rozwiąż nierówność: x – 1 <
6 x x2 .
Zadanie 4. (4 p.)
Rozwiąż równanie: |x2 – 1| – |x – 1| = 0.
Zadanie 5. (4 p.)
Wykaż, że dla dowolnych liczb rzeczywistych a i c, gdzie a0, równanie ax2 + (a + c)x + c = 0
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Zadanie 6. (6 p.)
Dla jakich wartości parametru m (mR) równanie x2 + (m + 2)x + m2 – 2m + 1 = 0 ma dwa
różne pierwiastki rzeczywiste ujemne?