Matura 2017P - zestaw I - Matematyka

Uwagi do materiału mogącego stanowić pomoc dla nauczycieli w przygotowaniu uczniów do
egzaminu maturalnego z matematyki z zakresu podstawowego.
1. Pragniemy pomóc państwu w przygotowaniu uczniów do egzaminu maturalnego
poprzez:
- podzielenie materiału powtórzeniowego na trzy etapy
- opracowanie zestawów zadań powtórzeniowych
- wskazówki metodyczne do wybranych zadań (trening twórczości)
- podanie treści zadań sprawdzianów podsumowujących każdy etap, wraz z odpowiedziami
- prezentację zadań z "najbliższego doświadczenia" (sprawdzian VI 2015, matura 2015)
2. W naszym rozumieniu propozycja ta może jedynie wzbogacać Państwa pracę i nie stanowi
zamkniętej całości, jest pewnym spojrzeniem doświadczonych nauczycieli i podpowiedzią dla
kolegów - nauczycieli jak można pracować z uczniami.
3. Zachęcamy do korzystania z konsultacji w powiatach z nauczycielami - liderami i tam pracą
nad tworzeniem i doskonaleniem własnego warsztatu nauczyciela - opiekuna ucznia
przygotowującego się do egzaminu maturalnego.
W szczególności, właśnie na takich spotkaniach można nauczyć się elementów treningu
twórczości i stosowania go w praktyce szkolnej.
4. Ważne jest, by każdy z Państwa opracował dla siebie i swoich uczniów pewną metodę
efektywnego przygotowania ucznia do egzaminu maturalnego - pomocne tutaj mogą być:
- liczne opracowania podręcznikowe , przykładowe arkusze, zbiory zadań powtórzeniowych,
- podręczniki typu - vademecum różnych wydawnictw,
- strony internetowe CKE, OKE czy
np. zadania. info (z zestawami zadań w wersji 8 - 9 tygodniowej przed samą maturą)
5. Ważną, naszym zdaniem, jest metoda "przerabiania" zestawów zadań maturalnych z
ostatnich lat - uczeń ma możliwość wyćwiczenia konkretnych umiejętności oraz opanowania
materiału podstawowego oraz wyćwiczenia go (Dobrze jak wie, jakie zadania są
najważniejsze! - wtedy chętniej skupia się na ich opanowaniu) - o tym będziemy chcieli
napisać w kolejnych materiałach.

Materiał powtarzany w I etapie
- Zestaw zadań
oraz komentarzy metodycznych, niekiedy elementów treningu:
I1. Liczby i wyrażenia
1. Uporządkuj rosnąco liczby:
a = 6(√3 + 3) – (1+2√3)
4
b = 2−
c = (2 + √3)2
√3
2. Oblicz:
a)
5∙37 −36 ∙2
13∙36
=
4
1
b) 125−3 ∙ √−64 ∙ 92
3
3. Udowodnij, że: log 3 75 = 1 + 2 log 3 5
4. Wyznacz wszystkie pary liczb naturalnych (a, b) spełniające równanie
log 3 𝑎 + log 3 𝑏 = 2
5. Liczba 240 to przybliżenie z nadmiarem pewnej liczby, a błąd bezwzględny tego
przybliżenia wynosi 8,76. Jaki jest błąd względny tego przybliżenia?
6. Dane są zbiory: A = ⟨−3; 5) oraz B = (1; 4⟩.
Wyznacz zbiory: 𝐴 ∪ 𝐵, 𝐴 ∩ 𝐵, 𝐴 − 𝐵, 𝐵 − 𝐴, 𝑅 − 𝐴, 𝑁 ∩ 𝐵
7. Mając dane: A   4, 0  2,4
oraz B   1,3 wyznacz:
𝐴 ∪ 𝐵, 𝐴 ∩ 𝐵, 𝐴 − 𝐵, 𝐵 − 𝐴
8. Oprocentowanie lokaty dwuletniej wynosi 4% w skali roku. Ile złotych trzeba
wpłacić na tę lokatę, aby po dwóch latach odsetki wyniosły 408 zł?
9. Oblicz wartość wyrażenia (√2 − 𝑥 + 2𝑥)(2𝑥 − √2 − 𝑥) dla x = - √2
10. Przekątna kwadratu jest o 4 cm dłuższa od boku tego kwadratu. Oblicz długość
boku kwadratu. Wynik przedstaw w postaci a +b √𝑐.
11. Wyznacz resztę z dzielenia przez 3 sumy kwadratów dwóch kolejnych liczb
naturalnych, niepodzielnych przez 3. Odpowiedź uzasadnij.
 Uwaga: Oczekujemy zastosowania postaci liczb całkowitych, warto więc
poświęcić więcej uwagi na ćwiczenie zadań z różnymi resztami;
Tutaj jest miejsce na własne "odkrycia" uczniów: Co będzie gdy, np. dodamy
do siebie kwadraty trzech kolejnych liczb nieparzystych? itp.
12.Wiadomo, że dla różnych od zera liczb a i b zachodzi związek:
Wyznacz wartość wyrażenia
4𝑎−3𝑏
2𝑎
= 6.
.
7𝑏
 Uwaga: Kolejne zadanie do poćwiczenia, np. Wiedząc, że
wyznacz wartość wyrażenia
10𝑎+5𝑏
𝑏−2𝑎
𝑎+𝑏
2𝑎+3𝑏
𝑎+4𝑏
=3,
. A w dalszej perspektywie "maturalnego"
powtarzania będziemy mieli podobne wyrażenia trygonometryczne typu:
𝑠𝑖𝑛𝑥−2𝑐𝑜𝑠𝑥
𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥
= 4, wyznacz tgx (lub odwrotnie), czy bardziej skomplikowane
zależności typu:
𝑥 2 −𝑥𝑦+𝑦 2
𝑥 2 +𝑥𝑦+2𝑦 2
3
=7 .
13.Zapisz wyrażenie w postaci potęgi liczby 3
1
3 9  
 81 
4
27  3 7
3
1
2

14. Dane są przedziały 𝐴 = (−∞, 𝑚2 − 6⟩, 𝐵 = ⟨5𝑚, +∞).
a) dla 𝑚 = −2 wyznacz 𝐴 ∪ 𝐵, 𝐴 ∩ 𝐵, 𝐵\𝐴.
b) wyznacz wszystkie wartości parametru m, dla których cześć wspólna tych
przedziałów jest zbiorem jednoelementowym
 Uwaga: Zadanie warto poprzedzić prostszymi zadaniami przyjmując za
przedziały odpowiednio np.
𝐴 = (−∞, 3⟩, 𝐵 = ⟨𝑚, +∞) ; 𝐴 = (−∞, 𝑚⟩, 𝐵 = ⟨4 − 𝑚, +∞).
A można też "utrudnić" modyfikując w kierunku, np. ... dla których
część wspólna jest przedziałem domkniętym o długości 1.
2
2
15. Dana jest liczba 𝑥 = (1 − 2√2) − (3 − √2) . Wyznacz liczbę odwrotną do
liczby x. Wynik przedstaw w postaci wyrażenia 𝑎 + 𝑏√2 , gdzie a, b są liczbami
wymiernymi.
 Uwaga: Zadanie warto poprzedzić zestawem prostszych zadań, np.
2
x = (3 − √2),x = (3 − √2) itd
5 −2
16. Wyznacz liczbę 𝑥 𝑎 , gdzie 𝑥 = −√3 i 𝑎 = 100 ∙ (2)
2
− 643 − 22 .
1



3
2

3
9


  2
17. Dany jest zbiór A = 1 ;
; 3 3 ; 1, (4);   ; 2 ; 1, (4) .
8
 16 
 11 5

a) Wypisz ze zbioru A liczby wymierne i przedstaw je w postaci ułamka
niewłaściwego nieskracalnego.
b) Uporządkuj wszystkie liczby ze zbioru A w kolejności od najmniejszej do
największej.
18. Niech x + y =12 i x2 + y2 = 126. Oblicz wartość wyrażenia x·y.
 Uwaga: Warto uczniom wspomnieć o tym, że dobrze jest pamiętać "wzór"
x2 + y2= (x + y)2 - 2xy. Także przy tym zadaniu można "twórczo" ćwiczyć
różne warianty - uczniowie mogą to robić! Np. "znając różnicę i sumę
kwadratów obliczyć iloczyn liczb", "znając sumę i sumę trzecich potęg
obliczyć iloczyn liczb"; lub odwracając "mając iloczyn i sumę kwadratów
liczb obliczyć ich sumę/różnicę"
19. Jakim procentem liczby 1,8 jest wartość wyrażenia
3
√64−(√7−2)(√7+2)
(0,75)−2 +(−1,5)−2
?
20. Suma kwadratu pewnej liczby i liczby od niej o 3 mniejszej jest równa 17.
Znajdź te liczby.
21. W prostokącie o bokach x i y długość boku x zwiększono o 25%, a długość boku
y zmniejszono o 20%. Jak zmieni się pole tego prostokąta?
2
3
22. Wykaż, że liczby: 𝑥 = 3−2√2 + 3+2√2 i 𝑦 = 2√2 − 15 są liczbami przeciwnymi.
I2. Zadania tekstowe
1. Cena towaru zwiększyła się najpierw o 20% następnie zmniejszyła się o 15%, a po
sezonie zmniejszyła się o 40%. Po tych zmianach cena wynosiła 183,60 zł. Oblicz
początkową cenę towaru.
2. Na lokacie bankowej ulokowano 2000 zł na okres 2 lat z kapitalizacją odsetek co 3
miesiące. Roczna stopa procentowa jest równa 8%. Jaka będzie wartość lokaty na
koniec okresu oszczędzania?
3 . Babcia rozdzieliła między wnuków wszystkie cukierki, jakie miała w torebce.
Pierwszemu wnukowi dała czwartą część wszystkich cukierków, drugiemu
natomiast szóstą część pozostałych. Trzeci wnuk otrzymał 50% tego, co zostało, a
czwarty dostał ostatnie 10 cukierków. Oblicz, ile cukierków miała babcia i po ile
otrzymali pierwszy, drugi i trzeci wnuk.
4. Na pewnym parkingu w Rzeszowie stoją tylko auta niebieskie i czerwone. Auta
czerwone stanowią 45% wszystkich aut na parkingu. Gdy 8 aut niebieskich
odjechało, na parkingu pozostało tyle samo aut niebieskich i czerwonych. Oblicz,
ile na początku na parkingu było wszystkich aut, a ile niebieskich.
5. Średni wiek pracowników pewnej firmy był równy 36 lat. Teraz, kiedy odszedł
jeden pracownik w wieku 45 lat, średnia wieku pozostałych wynosi 35 lat. Ile
osób pracowało wcześniej w tej firmie?
6. Piotrek jest o 10 lat starszy od swojego brata Pawła. Pięć lat temu Paweł miał 4
razy mniej lat niż Piotrek ma teraz. Ile lat miał Piotrek kiedy urodził się Paweł.?
Rozwiąż zadanie za pomocą układu równań.
7. Do magazynu dostarczono tyle jednakowych skrzynek jabłek, ile wynosiła waga
każdej skrzynki wyrażona w kilogramach. Po sprzedaniu 10 skrzynek okazało się,
że zostało jeszcze 600 kg jabłek. Oblicz, ile kilogramów jabłek dostarczono do
magazynu.
I3. Funkcje
2𝑥 − 1 𝑑𝑙𝑎 𝑥 ∈ ⟨−4; 2)
1. Dana jest funkcja f(x) = {
−𝑥 + 3 𝑑𝑙𝑎 𝑥 ∈ ⟨3; 5⟩
a) Naszkicuj wykres funkcji f b) Oblicz miejsca zerowe tej funkcji
1
c) Oblicz f(12) d) Z wykresu odczytaj zbiór rozwiązań nierówności f(x)≥ 1
e) Naszkicuj wykres funkcji g(x) = f(-x)
2. Wyznacz wzór funkcji liniowej, która spełnia podane warunki: f(2) = 3 i f(-1)=6
3. Miejscem zerowym funkcji f(x) = (k – 3)x + 3√3 jest liczba √3. Oblicz k.
 Uwaga: Zadanie warto poprzedzić prostszym: f(x) = (k-3)x - 4, x= -2
4. Wyznacz m wiedząc, że punkt przecięcia wykresów funkcji liniowych
f(x) = 2x – 4 i g(x) = -3x + 2m+3 leży na osi OY.
5. Dane są funkcje f(x) = -5x + 3 oraz g(x) = -2x +6. Oblicz, dla jakich argumentów
wartości funkcji f są mniejsze od wartości funkcji g.
6. Oblicz pole figury ograniczonej wykresami funkcji f(x) = -x + 3 i g(x) = 2x – 1
oraz osią OY.
7. Wyznacz punkty, w których prosta 2𝑥 + 5𝑦 − 20 = 0 przecina osie układu
współrzędnych.
4
Czy punkt 𝐴 = (8, 5) należy do tej prostej?
8. Zapisz wzór funkcji liniowej której wykres przechodzi przez punkty:
0,6, - 2, 4
 Uwaga: Niekiedy w zadaniach stawiajmy uczniów w "podchwytliwej"
sytuacji podając np. 0,6, - 2, - 6 albo 0,6, 0, 4
9. Dane są funkcje o wzorach f(x) = –2x + 1 oraz g(x) = 2x. Dla jakich argumentów
wartości funkcji f są większe od wartości funkcji g?
10. Napisz równanie prostej
a) równoległej
b) prostopadłej
do prostej o równaniu 𝑦 = 2𝑥 − 5 i przechodzącej przez punkt 𝑃 = (1,2)
11. Dana jest funkcja o wzorze f(x) = – 3 x + 2 + b, xR.
a) Wyznacz wszystkie takie b, dla których miejsce zerowe funkcji jest liczbą
większą od 2 3 .
b) Napisz wzór funkcji liniowej g, której wykres jest prostopadły do wykresu
funkcji f i przechodzi przez punkt A(–4 3 , 3).
 Uwaga: Zadanie trzeba koniecznie poprzedzić prostszym
12. Sekretarka prezesa pewnej firmy otrzymuje stałą pensję miesięczną w wysokości
1800 zł, premię uznaniową wysokości 10% oraz dodatkowe wynagrodzenie za
nadgodziny. W styczniu miała 20 nadgodzin i otrzymała wraz z premią 2220 zł.
a) Oblicz stawkę za godzinę nadliczbową
b) Napisz wzór funkcji wyrażającej wynagrodzenie sekretarki (z premią) w
zależności od liczby przepracowanych godzin nadliczbowych.
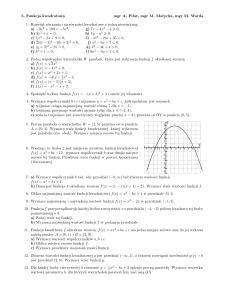
13. Poniżej przedstawiono wykres funkcji f.
a) Podaj zbiór wartości funkcji f.
b) Podaj miejsce zerowe funkcji g określonej wzorem g(x) = f(x – 2).
2 x  5 dla x   ,  1
14. Dana jest funkcja f(x) = 
.

x

2
dla
x


1
,


)

a) Oblicz miejsca zerowe funkcji.
b) Oblicz współrzędne punktu w którym wykres przecina oś OY.
15. Dana jest funkcja o wzorze f(x) = (2 – 3a )x + 1, xR.
a) Wyznacz a tak, aby miejscem zerowym funkcji była liczba 4.
b) Wyznacz wszystkie wartości a, dla których funkcja jest malejąca
c) Dla a = –1 napisz wzór funkcji liniowej, której wykres jest prostopadły do
wykresu danej funkcji i przechodzi przez punkt A(–5, 8).
16. Rozwiązaniem układu równań {
𝑎𝑥 + 𝑏𝑦 = 9
jest para liczb x = 3 i y = -1.
𝑏𝑥 − 𝑎𝑦 = 13
Wyznacz a i b.
17. Podaj wzór funkcji liniowej, której wykres przecina oś OY w punkcie A(0, 3) i
jej miejscem zerowym jest liczba 9.
18. Dane są wzory funkcji liniowych: f(x) = (2-k)x – 4, h(x) = (2k – 3k2) x – 7.
Wyznacz k tak, aby wykresy funkcji f oraz h były równoległe.
I4. Funkcja kwadratowa
1. Do wykresu funkcji kwadratowej f(x) = ax2 + bx + c należy punkt A(4, -5) , a
dla argumentu 6 funkcja przyjmuje największą wartość równą 3. Wyznacz
wartości współczynników a, b i c.
2. Wyznacz zbór wszystkich argumentów, dla których funkcja liniowa f(x) = 2x – 3
przyjmuje wartości większe niż funkcja kwadratowa g(x) = x2 – 3x + 1.
3. Wykaż, że dla każdej liczby rzeczywistej m funkcja f(x) = x2 + mx + m – 1 posiada
miejsce zerowe.
 Uwaga: Warto dobierać uczniom zadania w których zachęcamy ich do
"eksperymentów" typu: czy można wskazać jakieś (niezależne od m) miejsce
zerowe - pamiętamy zadanie z wielomianem na maturze rozszerzonej
"...wiedząc, że suma współczynników wielomianu wynosi 0 ...)!?!
4. Z drutu o długości 2 m budujemy model prostopadłościanu, którego podstawa jest
kwadratem. Jakie wymiary powinien mieć ten prostopadłościan, aby jego pole
powierzchni było największe?
5. Liczbę osób, które odwiedziły wystawę n - tego dnia od momentu jej otwarcia
opisuje wzór W(n) = – 6n2 + 60n – 50 , gdzie n N+ i 1  n  9.
a) W którym dniu wystawę odwiedziło najwięcej osób, i ile ich było?
b) Ile osób odwiedziło wystawę przez pierwsze trzy dni jej trwania?
6. Naszkicuj wykres funkcji 𝑓(𝑥) = −2𝑥 2 − 𝑥 + 1 . Na podstawie wykresu odczytaj:
a) zbiór wartości funkcji f
b) monotoniczność funkcji f
c) dla jakich argumentów funkcja przyjmuje wartości niedodatnie
7. Na jednym z osiedli mieszkaniowych znajduje się rabata kwiatowa w kształcie
trójkąta prostokątnego, którego przyprostokątne różnią się o 7 m. Powierzchnia
rabaty wynosi 30 m2. Ile metrów płotka potrzeba na ogrodzenie tej rabaty?
8. Oblicz największą i najmniejszą wartość funkcji 𝑓(𝑥) = 2𝑥 2 + 3𝑥 − 1
w przedziale ⟨−2,0⟩ .
 Uwaga: W niektórych zadaniach można (!) uczyć schematu: policz f(-2), f(0),
q i wybierz największą/najmniejszą z nich. W zakresie rozszerzonym przydaje
się taki schematyzm do zadań optymalizacyjnych: "dziedzina, warunek
łączący niewiadome, funkcja jednaj zmiennej, pochodna, warunek konieczny,
wystarczający, odpowiedź"
9. Rozwiąż nierówność: 4(𝑥 − 3)2 > 36 − 6𝑥
10. Liczby - 4 i 7 są miejscami zerowymi trójmianu 𝑦 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 i do wykresu
trójmianu należy punkt 𝐴 = (8, 36). Wyznacz parametry a, b, c.
11. Trójmian kwadratowy 𝑦 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 osiąga wartość największą równą -5 dla
argumentu 2 i do wykresu trójmianu należy punkt 𝐴 = (4, −7). Wyznacz
parametry a, b, c.
 Uwaga: Dla ucznia jest to niekiedy trudna sytuacja w jednej informacji są
ukryte dwie - trzeba podkreślić, że to nie jest "zwykły" punkt. W zakresie
rozszerzonym będzie to potrzebne przy zagadnieniach związanych ze styczną
i wykresem funkcji (czy ekstremum)
12. Dana jest funkcja 𝑓(𝑥) = (4𝑚2 − 25)𝑥 + 𝑚 + 1. Wyznacz wszystkie wartości
parametru m, dla których ta funkcja jest malejąca.
13. Obraz o wymiarach 3 m x 8 m chcemy oprawić w ramę o jednakowej szerokości.
Oblicz, jaką szerokość ramy należy dobrać, aby po oprawieniu pole obrazu wraz z
ramą wynosiło 50 m2?
14. Liczbę zachorowań na pewną chorobę w n – tym dniu trwania epidemii określa
wzór L(n) = -2n2 + 28n -1.
a) Ile osób zachorowało pierwszego i piątego dnia?
b) W którym dniu zachorowało najwięcej osób i ile ich było?
15. Wykres funkcji f danej wzorem 𝑓(𝑥) = −2𝑥 2 przesunięto wzdłuż osi OX o 3
jednostki w prawo i wzdłuż osi OY o 8 jednostek w górę, powstał wykres funkcji g.
a) rozwiąż nierówność 𝑓(𝑥) + 5 < 3𝑥
b) podaj zbiór wartości funkcji g.
16. Rozwiąż nierówność: 1  x  1 ( x  1) 2  ( x  7 )( x  7) .
2
2
 Uwaga: Warto w tym miejscu zwracać uwagę na potrzebę "dodawania"
nawiasu przed wyrażeniem poprzedzonym znakiem minus.
17. Rozwiąż równanie: (𝑥 2 − 5)(−2𝑥 2 − 3𝑥 + 5)(𝑥 2 + 1) = 0.
18. Funkcja kwadratowa określona jest wzorem f(x) = x2 – 3x + c. Oblicz f(1), jeśli
wiadomo, że f(-2) = 7.
19. Wykaż, że dla każdej liczby rzeczywistej a i dla każdej liczby rzeczywistej b
prawdziwa jest nierówność:
4𝑎2 − 4𝑎𝑏 + 3𝑏 2 ≥ 0.
 Uwaga: Podpowiadamy uczniom, żeby skupić swoją uwagę na jakimś
składniku, np. 4a2 = (2a)2 i dalej (2a-b)2 i brakuje 2b2, a to całkiem dobrze!
W zakresie rozszerzonym mieliśmy na maturze zadanie:
Udowodnij, że dla każdej liczby rzeczywistej x prawdziwa jest nierówność x4 - x2 -2x+3>0
Oczywiście jest ono zdecydowanie trudniejsze, ale warto zadać sobie pytanie:
jaki zestaw zadań skutecznie nauczy moich uczniów rozwiązywać takie
zadania?
20. Rozwiąż nierówność: (2𝑥 − 1)2 ≤ (3 − 2𝑥)(𝑥 − 2) + 2.
21. Na polu golfowym dwóch zawodników wybiło piłki, które zakreśliły w powietrzu
3
5
tory (łuki parabol) o równaniach ℎ1 (𝑥) = 60𝑥 − 7 𝑥 2 , ℎ2 (𝑥) = 50𝑥 − 8 𝑥 2 .
Która z piłek golfowych wzniesie się wyżej?
 Uwaga: Tutaj ciekawostka - warto postawić pytanie: dlaczego tutaj
h1(0)=h2(0) = 0?! Czytajmy: "Na polu golfowym ..."!
To już jest "koniec" zestawu? Niedokładnie - teraz jest czas i miejsce dla Ciebie
kolego nauczycielu - twórz własny zestaw zadań, zachęcaj do tego swoich uczniów a
ciekawymi pomysłami - dziel się z Nami !!!
 Matura 2015 (maj i czerwiec)
(niektóre zadania są zmodyfikowane dla potrzeb opracowania)
1. Rozwiąż nierówność:
-4≤x-1≤4
2. Określ liczbę rozwiązań równania:
x−1
x+1
= x-1
3. Określ zbiór wartości funkcji, której wykres przedstawiono poniżej:
4. Na wykresie funkcji liniowej określonej wzorem f(x) = (m-1)x +3 leży punkt S=(5,-2).
Wyznacz wartość m.
5. Funkcja liniowa f określona wzorem f(x)= 2x + b ma takie samo miejsce zerowe, jakie ma
funkcja liniowa g(x) = -3x + 4. Wyznacz wartość b.
6. Funkcja kwadratowa określona jest wzorem f(x) = x2+x+c.
Oblicz wartość f(1), wiedząc że f(3) = 4
2
x
7
14
7. Ile liczb całkowitych x spełnia nierówność: <
<
4
3
?
2
8. Dla jakiej wartości m prosta o równaniu y = m x +3 jest równoległa do prostej o równaniu
y = (4m-4)x - 3?
9. Dla jakiej wartości m prosta o równaniu y = 2mx -m2-1 jest prostopadła do prostej o
równaniu y = 4m2x +m2+1?
10. Średnia arytmetyczna zestawu danych: 2,4,7,8,9 jest taka sama, jak średnia arytmetyczna
zestawu danych: 2,4,7,8,9,x. Ile wynosi wartość x?
11. Rozwiąż nierówność: 2x2-4x > (x+3)(x-2)
12. Wyznacz najmniejszą i największą wartość funkcji kwadratowej f(x) = x 2-6x+3
w przedziale <0;4>
13. Jeśli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy połowę jego
licznika, to otrzymamy 4/7, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 1/2.
wyznacz ten ułamek.
14. Którą potęgą liczb 2 jest liczba 2√18 -√32 ?
15. Oblicz wartość wyrażenia:
16. Przy 23-procentowej stawce podatku VAT cena brutto samochodu jest równa 45 018 zł.
Jaka jest cena netto tego samochodu?
17. Wyrażenie 3a2-12ab+12b2 przekształcono do postaci 3x2. Ile wynosi x?
18. Określ liczbę rozwiązań równania 2x2 + 11x + 3 = 0
19. Na rysunku podany jest wykres funkcji f . Podaj przedział w którym funkcja f jest rosnąca.
Na rysunku przedstawiono wykres funkcji
.
20. Liczba 0,3 jest jednym z przybliżeń liczby
5
16
. Ile wynosi błąd względny tego przybliżenia,
wyrażony w procentach?
21. Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, jest równa , natomiast średnia
arytmetyczna zestawu danych: 2, 4, 7, 8, ,
jest równa
. Ile wynosi x?
2
22. Rozwiąż nierówność: 3x - 9x ≤ x - 3
23. Rozwiąż równanie: x (x2 - 2x +3) = 0
24. Udowodnij, że dla dowolnych liczb rzeczywistych x, y prawdziwa jest nierówność
3x2 + 5y2 - 4xy ≥ 0
25. Funkcja kwadratowa f dla x = -3 przyjmuje wartość największą równą 4. Do wykresu
funkcji f należy punkt A=(-1,3). Zapisz wzór funkcji kwadratowej f.
Zadanie 23
 Sprawdzian PCEN po drugiej klasie
1. Oblicz najmniejszą wartość funkcji kwadratowej f(x) = 2(x+3)(x-5) w przedziale <-6;4>.
2. Cenę aparatu, który początkowo kosztował 2000 zł dwukrotnie podniesiono o 10%, a następnie
dwukrotnie obniżono o 10%. cenę zaokrąglono do całych złotych. Jaka jest cena aparatu po tych
zmianach.
3. Wyznacz liczbę odwrotną do liczby 2 + √3.
4. Funkcja liniowa f(x) = -3x+2b przyjmuje wartości ujemne wtedy i tylko wtedy gdy x >3. Wyznacz
wartość parametru b.
5. Dla jakich wartości parametru m funkcja f(x) = (m2-4)x +2 jest malejąca?
6. Wyznacz zbiór dzielników liczby 232+230
7. Oblicz wartość wyrażenia (x - y)2 wiedząc, że x + y = 7 oraz x2 + y2 = 29
8. Wyznacz k we wzorze funkcji liniowej y = k x, wiedząc, że na jej wykresie leży wierzchołek
paraboli y = x2 +4x
9. Rozwiąż równanie:
x+2
2x+1
=
2
x+1
10. Funkcja f określona na zbiorze liczb całkowitych każdemu argumentowi przyporządkowuje liczbę
o 4 mniejszą od jego podwojonego kwadratu. Oblicz wartość f(-4).
11. Dla jakiej naturalnej wartości m cześć wspólna przedziałów
A = (−∞; 𝑚2 > i B = <m+12; +∞ ) jest zbiorem jednoelementowym?
We współpracy z koleżankami - nauczycielkami LO Sióstr Prezentek w Rzeszowie:
mgr Małgorzatą Kawałek, mgr Magdaleną Walicką i mgr Agnieszką Wąsowską
opracował dr Mariusz Kraus
Rzeszów 17 X 2015