Dyfrakcja promieniowania rentgenowskiego

Dyfrakcja promieniowania
rentgenowskiego
Podstawowa metoda badania struktury
ciał krystalicznych.
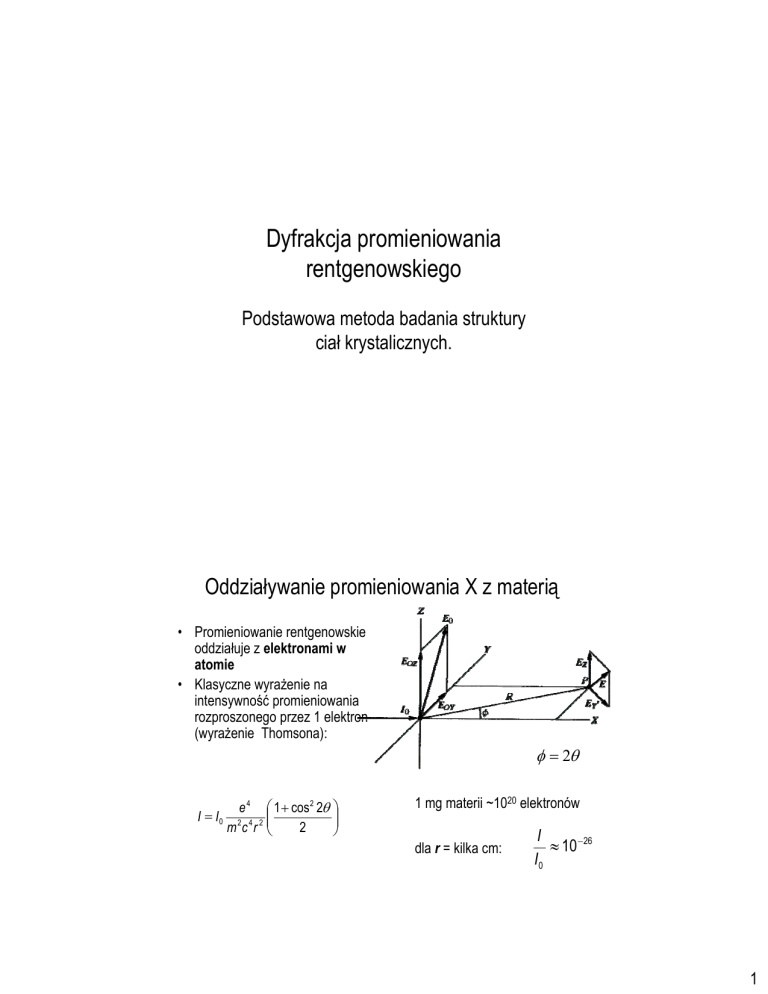
Oddziaływanie promieniowania X z materią
• Promieniowanie rentgenowskie
oddziałuje z elektronami w
atomie
• Klasyczne wyrażenie na
intensywność promieniowania
rozproszonego przez 1 elektron
(wyrażenie Thomsona):
φ = 2θ
I = I0
e 4 ⎛ 1 + cos 2 2θ ⎞
⎜
⎟⎟
2
m 2c 4 r 2 ⎜⎝
⎠
1 mg materii ~1020 elektronów
dla r = kilka cm:
I
≈ 10 −26
I0
1
Promieniowanie padając na atom ulega
rozproszeniu we wszystkich kierunkach. W
krysztale jest wiele atomów. Fale rozproszone
przez różne atomy mogą się albo wzmocnić, albo
osłabić.
Każdy atom staje się źródłem fali kulistej.
Fale, w niektórych kierunkach wzmacniają się, a
w niektórych wygaszają.
2
Dyfrakcja promieniowania rentgenowskiego na
krysztale
• Warunki wzmocnienia promieniowania:
– Warunek Braggów;
– Warunek Lauego;
– Konstrukcja Ewalda i równoważność obu warunków;
• Czynniki, od których zależy intensywność refleksów dyfrakcyjnych:
–
–
–
–
–
Rodzaj atomów;
Rozmieszczenie atomów w komórce (czynnik struktury);
Temperatura;
Kąt dyfrakcji;
Wielkość krystalitów.
Podejście Braggów:
kryształ traktujemy jak zespół równoległych płaszczyzn
sieciowych, oddziaływanie promieni X z kryształem jak odbicie
od zwierciadła.promieniowanie rentgenowskie wnika do wnętrza
kryształu i odbija się nie tylko od powierzchni, ale również od
kolejnych płaszczyzn kryształu.
3
Podejście Braggów:
promienie 1 i 2 przebywają różne drogi
1
∆s = 2l
2
l = d sinθ
∆s = 2d sinθ
promienie 1 i 2 się wzmocnią, jeżeli różnica dróg będzie:
RÓWNA CAŁKOWITEJ WIELOKROTNOŚCI DŁUGOŚCI FALI
Warunek dyfrakcji Braggów
2d hkl sin θ = nλ
Gdzie:
dhkl jest odległością między płaszczyznami
λ jest długością fali
n
θ - kątem odbłysku
n - liczba naturalna (tzw rząd refleksu dyfrakcyjnego)
4
Podejście Lauego
Laue traktował dyfrakcję promieni X tak jak dyfrakcję światła na siatce
dyfrakcyjnej, a kryształ jako zbiór atomów w 3D sieci krystalicznej.
Promienie 1 i 2, uginają się na
sąsiednich atomach, odległych od
siebie o a.
Promienie te, aby dotrzeć do
detektora, przebywają różne drogi.
Różnica dróg między 2 a 1 wynosi:
90o
detektor
Podejście Lauego
s1
1
s
α2
2
s2 − s1 = a cos α − a cos α 0
90o
α0
a
Aby promienie się wzmocniły, różnica dróg musi być równa całkowitej
wielokrotności długości fali. Zatem, warunek dyfrakcji:
a(cos α − cos α 0 ) = Hλ
5
Podejście Lauego
Analogicznie można rozważyć
detektor
kierunek prostopadły do
poprzedniego. Teraz promienie 1 i
2, uginają się na sąsiednich
90o
atomach, odległych od siebie o b.
Promienie te, aby dotrzeć do detektora,
również przebywają różne drogi.
β
b
β0
90o
Tym razem różnica dróg wynosi:
s2 − s1 = b cos β − b cos β 0
Warunek dyfrakcji, natomiast:
b(cos β − cos β 0 ) = Kλ
Podejście Lauego
Łatwo można zgadnąć, jak będzie wyglądał trzeci warunek Lauego.
Wszystkie trzy warunki muszą być spełnione jednocześnie. Zatem,
warunki Lauego dyfrakcji są następujące:
a(cos α − cos α 0 ) = Hλ
b(cos β − cos β 0 ) = Kλ
c(cos γ − cos γ 0 ) = Lλ
Gdzie H, K i L są liczbami całkowitymi, a kąty α0, β0, χ0 oraz α, β i γ
są odpowiednio kątami promienia padającego i ugiętego z osiami
krystalograficznymi a, b i c.
6
Podejście Lauego: inne sformulowanie
Wektor falowy promieniowania padającego: k0,
Wektor falowy promieniowania ugiętego: k
k0
k
Amplituda promieniowania rozproszonego
przez atom będący w p-kcie r (Ar), mierzona
w punkcie R:
Ar = A0e
i (k 0 r −ωt )
f
e
i (k 0 R − r
)
R −r
k
k0
A0: amplituda promieniowania padającego, f-czynnik atomowy
Podejście Lauego: inne sformułowanie
Gdy R>>r, |R-r|=R,
Rozpraszanie jest sprężyste: |k|= |ko|
r r r r r r r r rr
rr
k 0 R − r ≈ k (R − r ) = k R − k r ≈ k 0R − k r
Zatem:
e i (k 0R −ωt ) −KrRr v r r
Ar ≈ A0
fe , K = k − k 0
R
7
Podejście Lauego: inne sformułowanie
Czynnik jest taki sam dla wszystkich atomów
e i (k 0R −ωt ) − iKrRr v r r
Ar ≈ A0
fe , K = k − k 0
R
Ważnym czynnikiem, decydującym o wyniku dyfrakcji jest fexp(-iKR),
który zawiera różnicę faz między przyczynkami od różnych atomów.
Amplituda rozproszonego promieniowania jest, zatem proporcjonalna
do:
rr
A = ∑ fn e − iKrn
n
Gdzie suma przebiega po wszystkich atomach kryształu
Podejście Lauego: inne sformulowanie
Położenie n-tego atomu w krysztale można zapisać jako sumę
r r r
rn = rs + rb
Gdzie rs to położenie węzła sieci Bravais’g, a rb- położenie atomu
względem węzła sieci (baza atomowa).
rr
rr
⎛
⎞ ⎛
⎞
A = ⎜ ∑ e − iKrs ⎟ x ⎜ ∑ fb e − iKrb ⎟
⎝ s
⎠ ⎝ b
⎠
Gdzie suma przebiega po wszystkich atomach kryształu
8
Podejście Lauego: inne sformułowanie
rr
rr
⎞
⎞ ⎛
⎛
A = ⎜ ∑ e − iKrs ⎟ x ⎜ ∑ fb e − iKrb ⎟
⎠
⎠ ⎝ b
⎝ s
Obydwa składniki iloczynu muszą być różne od zera.
Drugi czynnik zawiera położenia atomów w komórce prymitywnej. Jest
to tzw. czynnik struktury.
rr
Fhkl = ∑ fb e − iKrb
b
Podejście Lauego: inne sformułowanie
rr
rr
⎞
⎞ ⎛
⎛
A = ⎜ ∑ e − iKrs ⎟ x ⎜ ∑ fb e − iKrb ⎟
⎠
⎠ ⎝ b
⎝ s
Obydwa składniki iloczynu muszą być różne od zera.
Pierwszy czynnik zawiera położenia węzłów sieci Bravais’go (wektory
translacji). Zapisując wektory translacji za pomocą wektorów
prymitywnych, otrzymujemy:
∑e
s
rr
− iKrs
= ∑e
ni
r r
− i Kn i a
∑e
nj
r r
− iKn j b
r r
∑ e − iKnk c
nk
9
Podejście Lauego: inne sformułowanie
∑e
s
rr
− iKrs
= ∑e
r r
− i Kn i a
ni
∑e
r r
− iKn j b
nj
∑e
r r
− iKnk c
nk
Dużą amplitudę promieniowania rozproszonego otrzymujemy, gdy
promieniowanie rozproszone na wszystkich węzłach sieci jest zgodne
w fazie (wszystkie wyrazy równe 1). Otrzymujemy 3 warunki:
rr
Ka = 2πh
rr
Kb = 2πk
rr
Kc = 2πl
Warunki Lauego
Podejście Lauego: inne sformulowanie
Wektor ten można zapisać w prostszy sposób:
r r
K = GHKL
Aby w danym kierunku (k) powstało maksimum dyfrakcyjne, różnica wektora
falowego promieniowania padającego i ugiętego musi być wektorem sieci
odwrotnej.
10
Co to oznacza?
• Każdy atom rozprasza padające promieniowanie we wszystkich
kierunkach, ale tylko pod niektórymi kątami nastąpi wzmocnienie
interferencyjne promieni. Tylko w tych kierunkach, w których
wektor dyfrakcji (k-k0) jest wektorem sieci odwrotnej.
Kula Ewalda
• Rysujemy wektor falowy promieniowania padającego, tak aby jego
koniec był w węźle sieci odwrotnej. Zakreślamy sferę (okrąg) wokół
tego punktu, o promieniu równym k = 2π/λ
Maksimum dyfrakcyjne
zaobserwujemy tylko tam,
gdzie kula przechodzi przez
węzeł sieci odwrotnej, czyli
tam gdzie K=G
11
Warunki: Lauego i Bragga są sobie równoważne.
2d sinθ = nλ
r
r r
k − k0 = GHKL
1.
Przez K oznaczamy
różnicę między wektorem falowym
promieniowania rozproszonego
(k) i padającego (k0)
K = k - ko
Warunki: Lauego i Bragga są sobie równoważne.
k i ko są równej długości 2π/λ,
k sinθ
Kąt między k i-ko jest 2θhkli
(hkl)
płaszczyzna (hkl) dzieli go na pół
Długość K jest zatem:
1
K = k sinθ
2
4π
K=
sinθ
λ
12
Warunki: Lauego i Bragga są sobie równoważne.
Jednocześnie, zgodnie z warunkiem Lauego, K jest wektorem sieci
odwrotnej GHKL. Zatem, jego długość:
K = GHKL
Ale, długość wektora sieci odwrotnej jest związana z odległością międzypłaszczyznową:
GHKL =
2π
dHKL
Otrzymujemy, zatem:
K=
2π
=
4π
λ
λ = 2dHKL sinθ
d HKL
sinθ
Warunek Bragga
Od czego zależy intensywność refleksu
dyfrakcyjnego?
Rodzaj atomów
Kąt dyfrakcji
Temperatura
Rozmieszczenie atomów w komórce elementarnej
Krotność płaszczyzn hkl
Czynnik polaryzacyjny
Absorpcja
2
IC (q ) = mALpK F (q ) + I b
13
Rodzaj atomu
Promienie X są rozpraszane przez elektrony.
Amplituda fali rozproszonej będzie tym
większa, im większa jest liczba Z atomu.
Definiuje się tzw. atomowy czynnik
rozpraszania
f=
amplituda fali rozproszonej przez atom
amplituda fali rozproszonej przez elektron
Rodzaj atomu
• Czynnik atomowy f = Z dla
dowolnego atomu przy
rozproszeniu do przodu (2θ =
0): I(2θ=0) =Z2
• Gdy θ wzrasta f maleje;
f=
amplituda fali rozproszonej przez atom
amplituda fali rozproszonej przez elektron
14
Kąt, pod jakim zachodzi dyfrakcja
Słabsze intensywności
-pod wyższymi kątami θ
- dla mniejszych długości fali λ.
Spadek intensywności jest większy dla
dużych atomów
15
Rozmieszczenie atomów w komórce
elementarnej (czynnik struktury)
• Struktura regularna prosta:
• W każdej równoległej płaszczyźnie atomy rozmieszczone są
identycznie.
• Np. w płaszczyznach (100):
Rozmieszczenie atomów w komórce
elementarnej (czynnik struktury)
• Struktura regularna centrowana objętościowo:
• W takiej strukturze, w płaszczyznach równoległych atomy
rozmieszczone są inaczej:
16
Fhkl = ∑ fb e
b
rr
− iKrb
Czynnik struktury
• O amplitudzie fali ugiętej spełniającej warunek Bragga decyduje
również sposób rozmieszczenia atomów w komórce elementarnej oraz
ich rodzaj.
• Wyraża się to za pomocą tzw. czynnika struktury (liczba zespolona):
Fhkl = ∑ f j e
2πi ( hx j + ky j + lz j )
j
gdzie fj jest atomowym czynnikiem rozpraszania j-tego atomu
Czynnik struktury
• O wielkości refleksu dyfrakcyjnego decyduje kwadrat czynnika
struktury. Jest to zwyczajna liczba rzeczywista.
⎛N
2
⎞
⎛N
⎞
⎟
⎜
∑ f j cos 2π (hx j + ky j + lz j ⎟ + ⎜ ∑ f j sin 2π (hx j + ky j + lz j ⎟⎟
⎝ j =1
⎠
⎝ j =1
⎠
2
2
Fhkl
=⎜
⎜
17
Przykład: jeden atom w węźle sieci
F = fe 2πi 0 = f
Czynnik struktury nie zależy od hkl.
Maleje wraz z f wraz ze wzrostem
sinθ/λ
Przykład: struktura bcc
Współrzędne atomów: (0, 0, 0) (½,½,½)
x1=0, y1=0, z1=0
x2=½, y2=½, z2=½
2
2
Fhkl
⎞
⎛ N
⎞
⎛ N
= ⎜ ∑ fn cos 2π (hx n + ky n + lzn ⎟ + ⎜ ∑ fn sin 2π (hx n + ky n + lzn ⎟
⎟
⎜
⎟
⎜
⎠
⎝ n =1
⎠
⎝ n =1
2
2
Fhkl
= (fn [cos 0 + cos π (h + k + l )])2 + (fn [sin 0 + sin π (h + k + l )])2
18
Struktura bcc
Fhkl2 = ( f n [cos 0 + cos π (h + k + l )]) + ( f n [sin 0 + sin π (h + k + l )]) =
2
2
2
2
f n (1 + 1) 2 + f n (0 + 0) 2 = 4 f n2
gdy h+k+l = liczby parzyste (2n)
Fhkl2 = ( f n [cos 0 + cos π (h + k + l )]) + ( f n [sin 0 + sin π (h + k + l )]) =
2
2
2
2
f n (1 − 1) 2 + f n (0 + 0) 2 = 0
gdy h+k+l = liczby nieparzyste
(2n+1)
prymitywna
fcc
bcc
19
Czynnik polaryzacyjny
• Czynnik polaryzacyjny wynika stąd, że elektron rozprasza
promieniowanie w dowolnym kierunku, a nie w kierunku drgań.
Czynnik polaryzacyjny, przy niespolaryzowanym promieniowaniu
padającym
1 + cos 2 2θ
p=
2
Temperatura
• Im wyższa temperatura, tym większa amplituda drgań atomów.
Chmura elektronowa ma mniejszą gęstość: drgania termiczne osłabiają
intensywność promieni ugiętych.
Czynnik temperaturowy
wyraża się wzorem:
⎡ sin2 θ ⎤
exp ⎢− B 2 ⎥
λ ⎦
⎣
Gdzie B jest związane
ze średnim kwadratem
amplitudy drgań atomu
B = 8π 2 × u 2
20
Scattering by C atom expressed in electrons
Czynnik temperaturowy
Krotność płaszczyzn
• Krotność płaszczyzn wynika z faktu, że w krysztale są płaszczyzny
o różnych orientacjach,ale o tym samymch wartościach d i F 2
100, 1 00, 010, 0 1 0, 001, 00 1
110, 1 10, 1 1 0, 1 1 0, 101, 10 1, 1 0 1, 1 01, 011, 0 1 1, 01 1, 0 1 1
111, 11 1, 1 1 1, 1 11, 1 1 1, 1 1 1, 1 1 1, 1 1 1
p100 = 6
p110 = 12
p111=8
21
Absorpcja
• Zależna od kąta absorpcja promieniowania wewnątrz próbki modyfikuje
intensywność maksimów dyfrakcyjnych.
Czynnik absorpcyjny dla grubej próbki:
Czynnik absorpcyjny dla cienkiej warstwy:
A=
1
2µ
⎛ 2 µτ ⎞
A = 1 − exp⎜ −
⎟
⎝ sinθ ⎠
Gdzie µ jest współczynnikiem absorpcji, a τ grubością próbki
Metody eksperymentalne
Wszystkie metody można przedstawić w następujący sposób:
Źródło
Promieni
X
Próbka
Detektor
22
Próbką może być:
• monokryształ
• polikryształ
W zależności od tego, czy próbka jest mono- czy polikrystaliczna,
stosuje się różne metody badań.
Metody badania struktury monokryształów
Metoda Lauego
Metoda obracanego kryształu
Metoda Lauego
Źródło
promieniowani
a X o widmie
ciągłym
(wszystkie
długości fali)
Klisza
fotograficzna
lub detektor
powierzchniowy
Kolimator
Nieruchomy
kryształ
23
Metoda Lauego
Rejestruje się promienie albo
po przejściu przez kryształ,
albo odbite od kryształu
Każdy punkt odpowiada innej
rodzinie płaszczyzn sieciowych
Metoda Lauego
Na podstawie odległości między
punktami można wyznaczyć:
a) odległości międzypłaszczyznowe, a co za tym idzie,
rozmiar komórki elemen1/b
tarnej
b) Orientację kryształu
1/a
c) Symetrię komórki
elementarnej
d) Niektóre defekty strukturalne.
24
Metoda obracanego kryształu
Badanie próbek polikrystalicznych:
dyfraktometr rentgenowski lub kamera Debye’a Scherrera
25
Badanie próbek polikrystalicznych
Krystality w polikrysztale ustawione są przypadkowo. Zawsze któryś
jest zorientowany tak, że spełnia warunek dyfrakcji dla którejś rodziny
płaszczyzn sieciowych
Detektor
Monochromatyczne
promienie X
• Klisza
• Licznik
Film: kamera Debye’a Scherrera
Promień kamery = R
S
4θ
=
2πR 360
26
Licznik - Dyfraktometr
Detektor
Szczeliny Sollera
szczeliny
Lampa
Monochromator
Szczeliny Sollera
szczeliny
maska
Polikrystaliczna
próbka
szczeliny
o
0.5
Cu2O
Cu2O
CaO
1.0
2201
2201
1.5
Sr10Bi6O24
2201
Wynik pomiaru może wyglądać np. tak:
850 C
0.0
Intensity [a.u.]
1.5
1.0
o
700 C
0.5
0.0
1.5
glas s
szkło
1.0
0.5
0.0
20
30
40
50
2θ
27
Wszystkie przyrządy rentgenowskie
zbudowane są z podobnych elementów:
Promieniowanie X jakoś trzeba wytworzyć,
zmonochromatyzować i zmierzyć jego intensywność
Lampa rentgenowska
Promieniowanie rentgenowskie wytwarzane w
lampie jest dwojakiego rodzaju:
promieniowanie hamowania (ciągłe)
promieniowanie charakterystyczne
(konkretne długości fali)
28
Promieniowanie rentgenowskie
Promieniowanie charakterystyczne
29
Monochromatyzacja promieniowania
W dyfraktometrze proszkowym, oraz metodzie obracanego
kryształu chcemy mieć promieniowanie monochromatyczne ( Kα )
musimy pozbyć się Kβ oraz promieniowania hamowania.
Stosuje się dwie metody:
I
Filtry
Monochromatory
E
λλ
Monochromatyzacja promieniowania: filtry
Ich działanie polega na absorbcji promieniowania:
Np. miedź
emisja
absorpcja
30
Monochromatyzacja promieniowania: filtry
Potrzebujemy pierwiastek, który absorbuje Kβi promieniowanie ciągłe,
ale przepuszcza Kα
Zazwyczaj, używa się
pierwiastka o Z
mniejszym o 1 lub 2 od
pierwiastka materiału
anody.
Filtry: przykład
Krawędź absorbcji Ni
Kα
Kα
Kβ
Kβ
1.2
1.4
1.6
λ in Å
(a) No filter
1.8
1.2
1.4
1.6
1.8
λ in Å
(b) With Ni filter
31
Monochromatory
Jest to kryształ (kwarc, german, ...) silnie odbijający promieniowanie od
jednej rodziny płaszczyzn. Kryształ ten orientuje się pod kątem Bragga
odpowiednim dla promieniowania Kα1
λ = 1.540 Å = 2dhklsinθ
Przykład: Monochromator jest kryształem Ge wyciętym równolegle
do płaszczyzn (111). Ge jest kryształem regularnym o stałej sieci
a=5.66Å. Oblicz kąt, pod jakim należy ustawić ten kryształ
względem wiązki promieniowania wytwarzanej przez lampą, aby
otrzymać tylko promieniowanie CuKα1.
1 h 2 + k 2 + l2
3
=
=
2
2
d
a
(5.66) 2
λ=2d sinθ
d=3.27Å
λ=1.540 Å
⎛ 1.540 ⎞
⎛ λ ⎞
⎟⎟
θ = sin −1 ⎜ ⎟ = sin −1 ⎜⎜
×
2
d
(
2
3
.
27
)
⎝ ⎠
⎝
⎠
= 13.62°
32
Monochromator germanowy dla
promieniowania o długości fali
λ=1.540 Å
13.62°
d=3.27Å
Detektory promieniowania rentgenowskiego
• W ogólności, podstawą detekcji promieniowania X czyli fotonów o
energii 5-25 keV jest fakt, że wzbudzają one elektrony w materiale
detektora. Wskutek tego może nastąpić:
– Jonizacja gazu
– Generacja par elektron-dziura w półprzewodniku
– Fluorescencja
– Procesy chemiczne
33
Jonizacja gazu
Jony utworzone wskutek napromieniowania biegną w stronę drutu, do którego
przyłożone jest wysokie napięcie. Gdy dotrą do elektrody, powodują impuls
prądu.
Jonizacja gazu
Najczęściej stosowane gazy:
Argon-Metan;
Ksenon-Metan;
Neon-Metan
34
Detektor scyntylacyjny
1.
Foton promieniowania X powoduje emisję światła z kryształu NaI
domieszkowanego talem.
2.
Fotony światła padając na fotokatodę wybijają z niej elektrony.
3.
Elektrony przyspieszane w polu elektrycznym wybijają z kolejnych
dynod kolejne elektrony.
4.
Płynie prąd, który jest proporcjonalny do natężenia mierzonego
promieniowania rentgenowskiego.
Informacje, które można otrzymać na podstawie
badania metodami dyfrakcji rentgenowskiej:
• Parametry komórki elementarnej;
• Symetria, sposób centrowania komórki elementarnej (czynnik
struktury);
• Skład fazowy wielofazowych substancji krystalicznych;
• Wielkość ziarna krystalicznego (mniejsze niż 0.1µm krystality
powodują poszerzenia refleksów dyfrakcyjnych);
• Naprężenia wewnętrzne;
• Tekstura (istnienie wyróżnionego kierunku krystalograficznego na
powierzchni materiału);
• Grubość i skład cienkich warstw;
• Rozszerzalność termiczna i przemiany fazowe (z badań w różnych
temperaturach).
35