Wyklad7

Wykład 7
7. Drgania elektromagnetyczne
7.1
Wstęp
Przypomnienie: masa M na sprężynie, bez
oporów. Równanie ruchu
M
d2 x
dt
Rozwiązania
2
 kx
x = Acost
v = dx/dt =-Asint
a = d2x/dt2 = – A2cost
przy warunku  = (k/M)1/2.
7.2
Obwód LC
Rozpatrzmy obwód złożony z szeregowo
połączonych indukcyjności L i pojemności C.
Opór omowy jest równy zeru (R = 0).
Załóżmy, że w chwili początkowej na
1
kondensatorze C jest nagromadzony ładunek
qm, a prąd przez cewkę jest równy zeru.
Energia zawarta w kondensatorze
WC = qm2/(2C)
(7.1)
jest maksymalna, a energia w cewce
WL = LI2/2
(7.2)
jest równa zeru.
Po
zamknięciu
obwodu,
kondensator
rozładowuje się przez cewkę. W obwodzie
płynie prąd I = dq/dt. W miarę jak maleje
ładunek na kondensatorze maleje też energia
zawarta w polu elektrycznym kondensatora, a
rośnie energia pola magnetycznego, które
pojawia się w cewce w miarę narastania w niej
prądu.
Wreszcie gdy ładunek spadnie do zera cała
energia jest przekazana do pola magnetycznego
cewki. Prąd w cewce indukcyjnej ma
maksymalną wartość. Ten prąd ładuje
kondensator (przeciwnie) więc energia jest
ponownie przekazywana do kondensatora. Stan
końcowy jest taki jak początkowy tylko
kondensator jest naładowany odwrotnie.
2
Sytuacja powtarza się. Mamy więc do czynienia
z oscylacjami ładunku (prądu).
Opis ilościowy
Z prawa Kirchoffa
UL + UC = 0
dI q
L
 0
dt C
Ponieważ I = dq/dt więc
d2 q
q
L

2
C
dt
(7.3)
(7.4)
To
jest
równanie
analogiczne
do
przypomnianego równania dla sprężyny, przy
czym następujące wielkości są analogiczne
q  x, L  M, 1/C  k
Tak więc możemy napisać rozwiązanie tego
równania
q = qmcost
3
I = dq/dt = -qmsint =-Imsint
 = (1/(LC))1/2
(7.5)
gdzie Im = qm
UL =LdI/dt = -LImcost
UC = q/c = (qm/C)cost
Ponieważ
LIm = Lqm2 = Lqm(1/(LC)) = qm/C
widać, że amplitudy napięć są takie same.
7.3
Obwód szeregowy RLC
Dotychczas rozważaliśmy obwód zwierający
indukcyjność L oraz pojemność C. Tymczasem
każdy obwód ma pewien opór R, przykładowo
jest to opór drutu z którego nawinięto cewkę.
Obecność oporu w obwodzie powoduje straty
energii w postaci wydzielającego się ciepła.
Energia zawarta w obwodzie maleje i
otrzymujemy drgania tłumione analogiczne do
drgań tłumionych sprężyny, przy czym
współczynnik tłumienia 1/(2) jest równy
R/(2L).
4
Drgania w obwodzie RLC można podtrzymać
jeżeli obwód będziemy zasilać napięciem
sinusoidalnie zmiennym
U (t )  U 0 sin t
Prawo Kirchhoffa dla obwodu zawierającego
elementy R, L, C oraz źródło SEM ma postać
dI
q
L  RI   U 0 sin t
(7.6)
dt
C
różniczkując po dt otrzymujemy
d2 I
dI I
L
R
  U 0 cos t (7.7)
2
dt C
dt
albo
U 0
d2 I R d I
I



cos t (7.8)
2
L d t LC
L
dt
To jest równanie analogiczne do równania dla
oscylatora wymuszonego przy R/L  1/,
1/(LC)  02 oraz U0/L  0.
Rozwiązanie ma więc analogiczną postać
I  I 0 sin(t   ) .
Amplituda wynosi więc
U0
I0 
(7.9)
2
1 

R 2   L 

C 

5
a między napięciem i natężeniem prądu istnieje
różnica faz, dana równaniem
L 
tg 
1
C
(7.10)
R
Wyrażenie (7.9) ma postać prawa Ohma przy
czym stała proporcjonalności pomiędzy U0 i I0
1 

Z  R   L 


C


2
2
(7.11)
pełni analogiczną rolę jak opór R w prawie
Ohma. Wielkość Z nazywamy impedancją
(zawadą) obwodu.
Gdy zmienne sinusoidalne napięcie przyłożymy
q
do kondensatora to U 
C
Stąd
dU I

dt C
co dla U=U0sint daje
I
U 0 cos t 
C
Stąd
6
I  CU 0 cos t  CU 0 sin(t  90  )
Widać, że prąd wyprzedza napięcie na
kondensatorze o 90.
Maksymalny prąd I0 = U0(C) a stałą 1/(C)
pełniącą rolę analogiczną do oporu w obwodzie
prądu
stałego
nazywamy
reaktancją
pojemnościową.
XC = 1/(C)
(7.12)
Jeżeli
generator
napięcia
zmiennego
podłączymy do cewki indukcyjnej to
analogicznie można pokazać, że
U0
U0
I 
cos t 
sin(t  90  )
L
L
Prąd pozostaje za napięciem o 90, a reaktancja
indukcyjna ma wartość
XL = L
(7.13)
Zauważmy, że w obwodzie RLC, pomimo
połączenia szeregowego oporów omowego,
pojemnościowego i indukcyjnego ich opór
7
zastępczy (zawada) nie jest prostą sumą tych
oporów. Wynika to właśnie z przesunięć
fazowych.
Trzeba je uwzględnić przy dodawaniu napięć.
U = UR + UC + UL
czyli
U = I0Rsint - XCI0cost + XLI0cost
(na kondensatorze U pozostaje za I, na cewce U
wyprzedza I)
Stąd
U0
 R sin t  ( X L  X C ) cos t
I0
Mamy teraz dodać sinus i cosinus graficznie tak
jak na rysunku obok Możemy przy tym
skorzystać z wyrażenia (7.10) według, którego
tg = (XL - XC)/R
.Relacja ta jest pokazana na rysunku poniżej
Zauważmy, ze przeciwprostokątna trójkąta na
rysunku jest równa zawadzie Z = (R2 + (XL XC)2)1/2.
Z
(XL - XC)

R
8
7.3.1 Rezonans
Drgania ładunku, prądu i napięcia w
obwodzie odbywają się z częstością zasilania .
Amplituda tych drgań zależy od  i osiąga
maksimum dla pewnej charakterystycznej
wartości tej częstości. Przypomnijmy, że
zjawisko to nazywamy rezonansem. Dla małego
oporu R czyli dla małego tłumienia warunek
rezonansu jest spełniony gdy
  0 
Natężenie prądu osiąga
maksymalną równą
I0 
U0
R
1
LC
wtedy
(7.14)
wartość
(7.15)
Widzimy, że natężenie prądu w obwodzie jest
takie, jak gdyby nie było w nim ani pojemności
ani indukcyjności, a zawada wynosiła R.
Przykład
Drgania wymuszone w obwodzie można także
wywołać bez włączania bezpośredniego źródła
SEM w postaci generatora. Przykładem może
9
być układ RLC w obwodzie wejściowym
radioodbiornika (telewizora) pokazany na
rysunku poniżej. Układ ten jest zasilany
sygnałem z anteny.
W układzie
dostrojenie do
częstotliwości danej
radiostacji jest
osiągane przez
dobranie pojemności.
W ten sposób jest
spełniony warunek
rezonansu dla tej częstotliwości. Przyjmijmy, że
w pokazanym układzie R = 10 , a L = 1 H.
Sprawdźmy, jaka powinna być pojemność C
aby uzyskać dostrojenie odbiornika (rezonans)
do stacji "Jazz Radio", która w Krakowie
nadaje na częstotliwości 101 MHz?
Korzystając z warunku (7.14) otrzymujemy
C = 2.48 pF.
W warunkach rezonansu napięcie na
kondensatorze (w obwodzie RLC) jest równe
U0 1
U0
U C ,rez  I 0 X C 

R  0C
R
L
C
10
Jeżeli sygnał wejściowy z anteny ma amplitudę
100 V to napięcie na kondensatorze przy
częstotliwości rezonansowej ma wartość 6.35
mV. Dla porównania napięcie na kondensatorze
przy tych samych ustawieniach R, L, C i
sygnale o tej samej amplitudzie ale o
częstotliwości 96.0 MHz (radio "RMF") wynosi
1 mV.
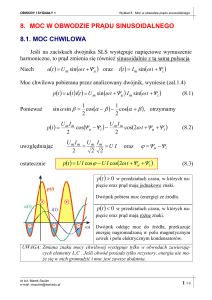
7.3.2 Moc w obwodzie prądu zmiennego
W obwodzie prądu przemiennego moc dana
analogicznym wyrażeniem jak dla prądu stałego
P(t )  U (t )I (t )
(7.16)
ale wartość jej zmienia się bo zmienne jest
napięcie i natężenie prądu. Dlatego też w
przypadku prądu zmiennego posługujemy się
wartościami średnimi. Zgodnie z naszymi
obliczeniami moc w obwodzie RLC w dowolnej
chwili t wynosi
P(t )  U (t ) I (t )  U 0 I 0 sin t sin(t   )
Korzystając ze wzoru na sinus różnicy kątów
otrzymujemy
11
P(t )  U 0 I 0 sin  t (sin  t cos   cos  t sin  ) 
1
 U 0 I 0 (sin  t cos   sin 2 t sin  )
2
2
gdzie skorzystaliśmy z relacji
sin t cos t  sin 2t 2 .
Moc średnia jest więc dana wyrażeniem
1
P  U 0 I 0 (sin 2 t cos   sin 2t sin  )
2
Ponieważ
sin 2  t  cos 2  t  1
to
sin 2  t  cos 2  t  1 2
(wykresy
sinus
i cosinus są takie same, jedynie przesunięte o
/2). Ponadto sin 2 t  0 bo funkcja sinus jest
na przemian dodatnia i ujemna. Uwzględniając,
ponadto że U0 = ZI0 oraz cos   R Z
otrzymujemy wyrażenie na moc średnią
U0I0
( ZI 0 ) I 0 R I 02 R
P
cos  

2
2
Z
2
(7.17)
Jak widzimy, średnia moc zależy od
przesunięcia faz. Przypomnijmy, że dla prądu
stałego P = I2R. Z porównania tych dwóch
wyrażeń dochodzimy do wniosku, że moc
12
średnia wydzielana przy przepływie prądu
zmiennego o amplitudzie I0 jest taka sama jak
prądu stałego o natężeniu
I0
I sk 
(7.18)
2
Tę wielkość nazywamy wartością skuteczną
prądu zmiennego. Analogicznie definiujemy
skuteczną wartością napięcia prądu zmiennego
U0
U sk 
2
(7.19)
Mierniki prądu zmiennego (np. amperomierze i
woltomierze) odczytują właśnie wartości
skuteczne. Wartość napięcia 220 V w naszej
sieci domowej to wartość skuteczna.
Obliczyliśmy moc średnią wydzielaną w całym
obwodzie. Porównajmy ją teraz ze średnią
mocą traconą na oporze R
2
I
2
2
2
0R
PR  I (t )R  I 0 sin  t R 
2
Widzimy, że cała moc wydziela się na oporze
R, a to oznacza, że na kondensatorze i cewce
nie ma strat mocy. Zwróćmy uwagę, że ten
13
wniosek pozostaje w zgodności z naszymi
wcześniejszymi obliczeniami. Gdy w obwodzie
znajduje się tylko pojemność lub indukcyjność
(nie ma oporu omowego) to przesuniecie
fazowe jest równe
/2, a ponieważ
cos( /2) = 0 to zgodnie z równaniem (7.16)
średnia moc jest równa zeru. Jednocześnie
zauważmy, że moc chwilowa zmienia się z
czasem; raz jest dodatnia (energia jest
gromadzona w polu elektrycznym kondensatora
lub magnetycznym cewki), a raz ujemna
(zgromadzona moc jest oddawana do układu).
Omawiane obwody, w których elementy R, L,
C stanowiły odrębne części nazywamy
obwodami o elementach skupionych. W
praktyce jednak mamy do czynienia
z elementami, które mają złożone własności.
Przykładem może tu być cewka, która oprócz
indukcyjności L ma zawsze opór R oraz
pojemność międzyzwojową C. Mamy wtedy do
czynienia z obwodami o elementach
rozłożonych.
14