Wyznaczanie odkształceń napięć i prądów. Źródła i sposoby

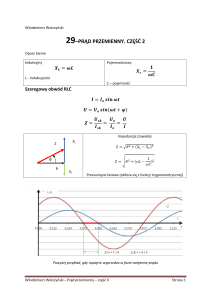
Wyznaczanie odkształceń napięć i prądów. Źródła i sposoby
poprawy odkształceń napięć i prądów. Moce i współczynniki mocy.
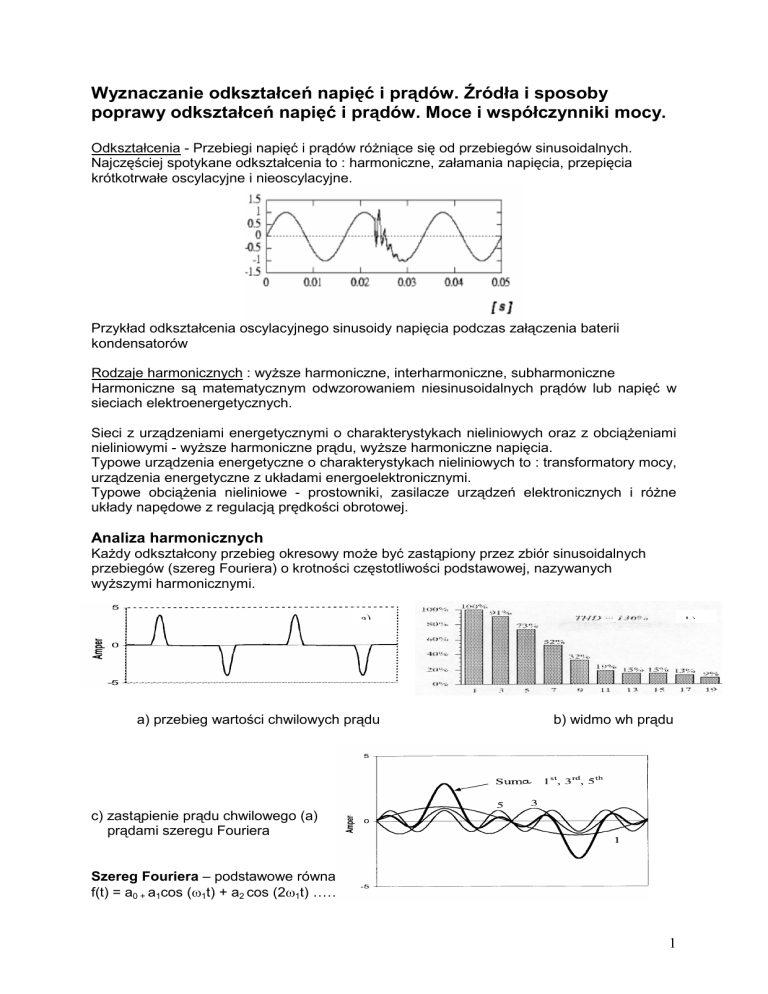
Odkształcenia - Przebiegi napięć i prądów róŜniące się od przebiegów sinusoidalnych.
Najczęściej spotykane odkształcenia to : harmoniczne, załamania napięcia, przepięcia
krótkotrwałe oscylacyjne i nieoscylacyjne.
Przykład odkształcenia oscylacyjnego sinusoidy napięcia podczas załączenia baterii
kondensatorów
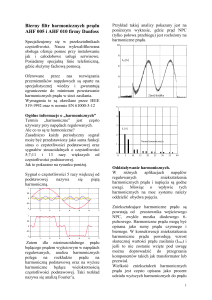
Rodzaje harmonicznych : wyŜsze harmoniczne, interharmoniczne, subharmoniczne
Harmoniczne są matematycznym odwzorowaniem niesinusoidalnych prądów lub napięć w
sieciach elektroenergetycznych.
Sieci z urządzeniami energetycznymi o charakterystykach nieliniowych oraz z obciąŜeniami
nieliniowymi - wyŜsze harmoniczne prądu, wyŜsze harmoniczne napięcia.
Typowe urządzenia energetyczne o charakterystykach nieliniowych to : transformatory mocy,
urządzenia energetyczne z układami energoelektronicznymi.
Typowe obciąŜenia nieliniowe - prostowniki, zasilacze urządzeń elektronicznych i róŜne
układy napędowe z regulacją prędkości obrotowej.
Analiza harmonicznych
KaŜdy odkształcony przebieg okresowy moŜe być zastąpiony przez zbiór sinusoidalnych
przebiegów (szereg Fouriera) o krotności częstotliwości podstawowej, nazywanych
wyŜszymi harmonicznymi.
a)
a) przebieg wartości chwilowych prądu
b)
b) widmo wh prądu
c) zastąpienie prądu chwilowego (a)
prądami szeregu Fouriera
Szereg Fouriera – podstawowe równanie :
f(t) = a0 + a1cos (ω1t) + a2 cos (2ω1t) …….+ b1sin (ω1t) + b2sin (2ω1t) + …..
1
= a0 + Σancos (nω1t) + ……. Σ bnsin(nω1t)
f(t) jest funkcją okresową o częstotliwości podstawowej ω1.
Składowe symetryczne wyŜszych harmonicznych
h=1
+
h=2
-
h=3
0
h=4
+
h=5
-
h=6
0
h=7
+
h=8
-
h=9
0
h=10
+
h- rząd wyŜszej harmonicznej
+, -, 0 – składowe symetryczne : zgodna, przeciwna, zerowa.
W sieciach trójfazowych cztero – lub pięcioprzewodowych niskiego napięcia (np. typu TT,
TN-C, TN-S) przepływ prądów odkształconych z wh prądów fazowych rzędu 3 oraz krotności
3 powoduje pojawienie się prądu w przewodzie PEN lub N (dalej nazywanego prądem
neutralnym).
Wartość skuteczna prądu neutralnego jest sumą algebraiczną prądów tworzących układ
składowych symetrycznych zerowych (0). Pozostałe harmoniczne (układ zgodny i przeciwny)
nie wpływają na wartość prądu neutralnego.
Prawo Ohma w zapisie wektorowym - dla poszczególnych wh w sieci rozgałęzionej - wyraŜa
zaleŜność :
Uh = Ih Zh
gdzie :
Uh – wektor napięcia węzłowego dla wh rzędu h,
Ih – wektor prądu węzłowego dla wh rzędu h,
Zh – macierz impedancji własnych i wzajemnych,
h – rząd wh (1, 2, 3,...).
Podstawowe miary wh
Wartości skuteczne napięć i prądów odkształconych, stopnie udziału wh (u), współczynniki
udziału wh (THD), moce elektryczne.
Wartość skuteczną (ARMS dalej A) napięcia lub prądu odkształconego oblicza się ze wzoru
h=k
ALi =
∑A
h =1
2
h, Li
= A1,Li
1 + (THD A ,Li / 100) 2
gdzie :
Ah,Li – wartość skuteczna harmonicznej napięcia lub prądu rzędu h w fazie Li ; A≡{U ∪ I}, i=1
dla obwodu elektrycznego jednofazowego lub i=1 ∪ 2 ∪ 3 dla obwodu elektrycznego
trójfazowego,
h- rząd wh (1, 2, 3,...k); k - największy rząd wh określany wg stosownego dokumentu
technicznego, zawierającego ocenę wh,
THDA,Li - współczynnik zawartości wh parametru A; wyraŜony w %.
2
Współczynnik udziału (uA,h) poszczególnych wh w harmonicznej podstawowej napięcia lub
prądu określa zaleŜność
uA,h,Li =
A h ,Li
A1,Li
100% .
Współczynnik zawartości wh napięcia (THDu) lub prądu fazowego (THDI) oblicza się ze
wzoru
h =k
∑A
THDA,Li =
h=2
2
h , Li
h=k
100% =
A 1,Li
∑ (u
h =2
A , h , Li
/ 100) 2 100%
A 1,L,i – wartość skuteczna harmonicznej podstawowej napięcia lub prądu (h=1) w fazie Li,
uA,h,Li - stopień udziału poszczególnych wh w harmonicznej podstawowej; wyraŜony w %.
Współczynnik odkształcenia napięcia lub prądu (TFF) określa wzór
h =k
∑A
TFFA,Li =
h =1
2
h , Li
A 1,Li
=
1 + (THD A ,Li / 100) 2
Współczynnik amplitudy (szczytu) napięcia lub prądu (TCF) oblicza się z zaleŜności
TCFLi =
A S,Li
A Li
100%
gdzie :
AS,Li – maksymalna wartość skuteczna prądu w fazie Li.
JeŜeli przebieg napięcia lub prądu jest sinusoidalny to TCFLi =1,414. Przy przebiegach
odkształconych TCFLi jest róŜne od 1,414.
Rezonans wh harmonicznych
Rezonans moŜna zdefiniować jako stan obwodu elektrycznego, w którym reaktancja
odbiornika lub susceptancja odbiornika są równe zeru.
JeŜeli w odbiorniku istnieje szeregowe połączenie elementów R, C, L i jest prawdziwy
warunek X=0, to występuje rezonans szeregowy nazywany równieŜ rezonansem napięć.
JeŜeli w odbiorniku istnieje równoległe połączenie elementów R, C, L i występuje warunek
B=0 to odbiornik jest w stanie rezonansu równoległego nazywanego równieŜ rezonansem
prądów.
Trójkąty rezystancji: a) ωL >
1
1
; b) ωL <
ωC
ωC
Z analizy trójkątów rezystancji przedstawionych na rysunku
rezonansu, tzn. ωL =
wynika, Ŝe dla przypadku
1
prawdziwe są zaleŜności: ϕ=0, Z=R, czyli w obwodzie z
ωC
rezonansem nie ma przesunięcia fazowego między prądem i napięciem. Obwód zachowuje
się tak, jakby istniała w nim tylko rezystancja.
W stanie rezonansu moc czynna wynosi:
3
P = U I ⋅ cos ϕ = U I
a moc bierna:
Q = U I sin ϕ = 0
gdyŜ ϕ =0.
Oznacza to, Ŝe cała energia elektryczna pobrana przez obwód przekształca się w ciepło w
jego rezystancji R. Energia bierna przekazywana jest między elementami L i C z
pominięciem źródła.
Częstotliwość, przy której wystąpi rezonans nazywamy częstotliwością rezonansową fr.
Wartość częstotliwości fr otrzymamy z równania (2.4)
ωr =
1
LC
lub
fr =
1
2π LC
Rezonans równoległy
Rezonans szeregowy
Linia
Kondensatory
Źródło
harmonicznych
prądu
Źródło
harmonicznych
prądu
Uproszczony schemat układu
Elektryczny schemat zastępczy
Wzrost impedancji wypadkowej
(bardzo duŜa wartość).
Wzrost napięcia na impedancji.
Źródło
harmonicznych
prądu
Źródło
impedancyjne
Źródło
harmonicznych
prądu
Uproszczony schemat układu
Kondensatory
Kondensatory
Źródło
harmonicznych
prądu
Impedancja
linii
Kondensatory
Elektryczny schemat zastępczy
Redukcja impedancji wypadkowej do poziomu
rezystancji. Wzrost prądu w obwodzie
indukcyjność – pojemność.
W stanie rezonansu szeregowego, czyli rezonansu napięć, występuje równowaŜenie się
napięć na cewce i kondensatorze U L − U C = 0 . Przy pewnych wartościach rezystancji R,
indukcyjności L i pojemności C - napięcia UL i UC mogą przybierać stosunkowo duŜe
wartości, mimo Ŝe napięcie zasilające obwód U jest stosunkowo małe. Mówimy wówczas, Ŝe
w obwodzie występują przepięcia.
Przy częstotliwości rezonansowej f=fr wartości reaktancji XL i XC są sobie równe, a prąd I
osiąga największą wartość ograniczoną jedynie rezystancją R w obwodzie ( I r =
U
R
).
4
Napięcie UC osiąga wartość maksymalną dla częstotliwości tuŜ przed rezonansem,
natomiast napięcie UL tuŜ po rezonansie. Przy częstotliwości rezonansowej napięcia UC i UL
są sobie równe.
Przyczyną rezonansu szeregowego jest występowanie w obwodzie transformatora i
kondensatorów. Źródło harmonicznych prądu po stronie pierwotnej transformatora jest
przyczyną duŜych odkształceń napięcia po stronie wtórnej transformatora.
W rezultacie moŜe to doprowadzić do uszkodzenia kondensatorów, jeŜeli wydolność źródła
harmonicznych jest większa niŜ wartość znamionowa kondensatorów
Stosunek reaktancji indukcyjnej XL do rezystancji R obwodu nosi nazwę dobroci obwodu:
X L 2πfL
=
R
R
Q=
W stanie rezonansu równoległego, czyli rezonansu prądów mamy:
IL + IC = 0
co oznacza, Ŝe prądy w cewce i kondensatorze równowaŜą się.
W stanie rezonansu równoległego prąd I ma wartość minimalną ograniczoną przez
rezystancję R, natomiast prądy I L i I C równowaŜą się.
Dobroć obwodu równoległego związana jest zasadniczo ze stratami mocy w kondensatorze i
zaleŜy od stosunku rezystancji R od reaktancji XC. Dobroć Q =
Qr =
R
, w stanie rezonansu:
XC
R
R
=
X Cr X L r
oraz
I L r = I Cr =
U
X Lr
=
U
R
Qr = Ir Qr
Oznacza to, Ŝe przy rezonansie prądy IL i IC są Qr razy większe od prądu pobieranego przez
obwód co nosi nazwę przetęŜenia.
Uwzględnienie harmonicznych jest waŜne w projektowaniu sieci elektroenergetycznych.
Źródła wyŜszych harmonicznych prądu
Wszystkie obciąŜenia nieliniowe
Wszystkie obciąŜenia nieliniowe pobierają prądy o przebiegu odkształconym. Przykłady
takich obciąŜeń wymienione są poniŜej.
· Sprzęt radiowo-telewizyjny i komputerowy; odbiorniki te wyposaŜone są w róŜnej klasy
zasilacze z pojemnościowymi filtrami napięcia, w których prądzie znaczący udział maja
harmoniczne rzędu 3 i 5.
· Świetlówki, zwłaszcza coraz powszechniej stosowane świetlówki kompaktowe, wyposaŜone
w układ przemiennika częstotliwości; odbiorniki te pobierają prąd o bardzo szerokim
spektrum wyŜszych harmonicznych.
· RóŜnego rodzaju zasilacze, przede wszystkim zasilacze z przetwarzaniem energii (SMPS).
· Bezstopniowe regulatory prędkości obrotowej silników, np. silników elektronarzędzi.
· Elektroniczne sterowniki natęŜenia oświetlenia.
· Układy bezprzerwowego zasilania (UPS).
· Urządzenia z rdzeniami magnetycznymi czy na przykład transformatory, silniki.
Oddziaływanie odkształceń napięć i prądów na urządzenia elektryczne
1. Migotanie ekranów monitorów
2. Przegrzewanie się transformatorów przy niepełnym obciąŜeniu
5
3.
4.
5.
6.
7.
8.
9.
Straty w silnikach indukcyjnych
Przegrzewanie się przewodów na skutek zjawiska naskórkowości
Nieprawidłowe funkcjonowanie urządzeń sterujących procesami technologicznymi
PrzeciąŜanie sieci danych
Problemy z urządzeniami do poprawy współczynnika mocy
PrzeciąŜanie przewodów neutralnych
NiepoŜądane działanie zabezpieczeń
Przeciwdziałanie skutkom negatywnym oddziaływania odkształceń
1. UPS, generatory rezerwowe
2. Pomiary faktycznej wartości skutecznej
3. Zmniejszanie dopuszczalnych obciąŜeń urządzeń elektrycznych
4. Obwody wydzielone
5. Odpowiednio połączone i dobrane uzwojenia fazowe transformatorów mocy
6. Kable z Ŝyłami wielodrutowymi dla obciąŜeń harmonicznych
7. Wymiana przewodów instalacji elektrycznych
8. Podział odbiorników na kategorie
9. Stosowanie siatek ekwipotencjalnych
10. Filtry pasywne
11. Filtry aktywne
12. Zmiana systemu instalacji na TN-S
13. Zwiększenie przekroju przewodów neutralnych.
Moce i współczynniki mocy w układach elektroenergetycznych
Moce dla przebiegów sinusoidalnych napięcia i prądu
6
- moc czynna P = P1= U I cos ϕ ,
- moc bierna Q = Q1 = U I sin ϕ,
- moc pozorna S = U I = U1 I1,
- trójkąt mocy S2 = P2 + Q2,
- współczynnik mocy cos ϕ = P/S.
Przykład.
Silnik charakteryzują parametry :
Pn = 51 kW, cos ϕ = 0,86 , η = 0,91. Obliczyć moce elektryczne odpowiadające
wyszczególnionym danym.
P = 56 kW, S= 65 kVA, Q = 33 kvar
Wartości cos ϕ oraz tg ϕ dla powszechnie uŜywanych urządzeń elektrycznych
Rodzaj urządzenia
Typowy silnik indukcyjny przy obciąŜeniu : 0 %
25 %
50 %
75 %
100 %
Lampy Ŝarowe
Lampy fluorescencyjne (brak kompensacji))
Lampy fluorescencyjne (z kompensacją)
Lampy wyładowcze
Piece rezystancyjne
Piece indukcyjne
Piece dielektryczne
Zgrzewarki
Spawarki łukowe 1-fazowe statyczne
Spawarki łukowe generatorowe
Spawarki łukowe transformatorowe
Piece łukowe
Poprawę cos ϕ ilustruje poniŜszy schemat
cos ϕ
0,17
0,55
0,73
0,8
0,85
1
0,5
0,93
0,4 do 0,6
1,0
0,85
0,85
0,8 do 0,9
0,5
0,7 do 0,9
0,7 do 0,8
0,8
tg ϕ
5,8
1,52
0,94
0,75
0,62
0
1,73
0,39
2,29 do 1,33
0
0,62
0,62
0,75 do 0,48
1,73
1,02 do 0,48
1,02 do 0,75
0,75
ObciąŜenie
Moce dla przebiegów niesinusoidalnych napięcia i prądu
W ogólnym przypadku moc czynną elektryczną (średnią) oblicza się z zaleŜności
7
P=
1
u i dt
T ∫T
Jeśli napięcie i prąd są okresowymi funkcjami czasu, o tym samym okresie T, to moŜna je
rozłoŜyć na szeregi Fouriera. Wtedy moc czynną moŜna obliczyć z zaleŜności
P=
U n I n cos Φ n
∑
n
gdzie : n - rząd harmonicznej napięcia i prądu.
PowyŜsze zaleŜności bazują na fizycznym zjawisku mocy i energii elektrycznej.
Definicja mocy biernej wg Budeanu, szerzej stosowana i aprobowana jako standard ma
postać
Q=
∑U
I sin Φ n
n n
n
Zwykle moc ta jest oznaczana jako QB.
Moc pozorną wyraŜa zaleŜność
S=
∑U ∑I
2
n
n
2
S =
∑U ∑I
2
n
n
n
2
n
2
n
n
≥ (∑ U n I n cos Φ n ) 2 + (∑ U n I n sin Φ n ) 2
n
n
Trójkąt mocy jest ogólnie nie spełniony dla definicji mocy biernej wg Budeanu i dlatego musi
być wprowadzona dodatkowa moc nazywana mocą dystorsji D
D2 = S2 – P2 – Q2
S
DB
.
QB
.
P
Rys. Układ geometryczny mocy Budeanu
Najbardziej znana, oprócz definicji Budeanu, to defincja S. Fryzego.
Fryze definiuje moce jako funkcje czasu. Prąd dzieli na dwa składniki. Pierwszy ia jest
prądem o tym samym kształcie i kącie fazowym jak napięcie (prąd rezystancyjny); ma on
amplitudę taką, Ŝe Ia*U jest równe mocy czynnej. Drugi składnik prądu jest prądem
szczątkowym ir. Prądy spełniają równania
ia =
P
u
U2
ir = i - ia
JeŜeli prąd ir zostanie skompensowany, źródło będzie widoczne jako czysto rezystancyjne
obciąŜenie i współczynnik mocy będzie równy jedności. MoŜna wykazać, Ŝe ia i ir są
ortogonalne a ich wartości skuteczne spełniają zaleŜność
I2 = I2a + I2r
Moc pozorna moŜe być wtedy określona jako iloczyn wartości skutecznych prądu i napięcia
S2 = U2 I2 = U2 (I2a + I2r) = P2 + Q2
W opracowaniach moc bierna Fryzego jest często oznaczana jako QF i nazywana jest „mocą
fikcyjną”.
8
Współczynnik mocy, w przypadku przebiegów sinusoidalnych napięcia i prądu, nazywany
powszechnie cos ϕ , oblicza się z zaleŜności
cos ϕ =
P1
S1
=
P1
P1 + Q1 2
2
Współczynnik mocy, w przypadku przebiegów niesinusoidalnych napięcia i prądu oblicza się
z zaleŜności
λ=
P
S
P1 + ∑ Pi
=
i =2
UI
P1 + ∑ Pi
i =2
=
U 1 I 1 1 + ( THDU / 100 ) 2 1 + ( THD I / 100 ) 2
W większości przypadków zachodzą dwa warunki
1) P1+ ∑ Pi ≈ P1
2
2) THDU jest zwykle mniejsze niŜ 10 %, zatem U≈ U1.
Uwzględniając powyŜsze relacje we współczynniku mocy λ otrzymuje się
λ=
P1
U 1 I 1 1 + ( THD I / 100 ) 2
= cos ϕ
1
1 + ( THD I / 100 ) 2
zatem
λ < cos ϕ
9