politechnika częstochowska

POLITECHNIKA CZĘSTOCHOWSKA
INSTYTUT FIZYKI
Ćwiczenie O-2: „Pomiar promieni krzywizny soczewki
Płasko – wypukłej metodą Pierścieni Newtona”.
Gerega Paweł
Włodarska Katarzyna
Budownictwo
Studia dzienne, gr II
Rok 2008/2009
Częstochowa, 05 maja 2009
* Zagadnienia do opracowania:
1. Zjawisko dyfrakcji i interferencji światła.
2. Doświadczenie Younga. Warunki powstawania minimum i maksimum
interferencyjnego
3. Superpozycja fal, fale spójne, interferencja fal jako szczególny przypadek
superpozycji fal.
4. Powstawanie pierścieni Newtona. Wyprowadzić wzór na promień pierścienia
Newtona.
5. Regresja liniowa.
* Wprowadzenie teoretyczne:
Doświadczenie Younga jest eksperymentem, w którym możemy zaobserwować interferencje
dwóch fal, rozchodzących się z dwóch jednakowych otworów oświetlonych z jednego źródła
światła. Załóżmy, że wiązka światła monochromatycznego punktowego źródła światła Z pada
na przysłonę szczeliny S1 i S2, odległe od siebie o d. Za przysłoną mamy dwie fale
wychodzące z tych szczelin. Obie fale pochodzą w istocie ze wspólnego źródła światła Z,
mają więc taką samą fazę początkową i taką samą częstotliwość.
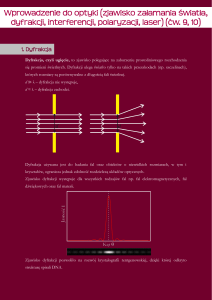
Dyfrakcja światła (inaczej ugięcie fal) polega na odchyleniu kierunku rozchodzenia się
światła od pierwotnego kierunku, kiedy przechodzi ono przez niewielkie szczeliny, otwory
lub natrafia na przeszkody. Kiedy promienie świetlne przechodzą przez wąską szczelinę,
uginają się na boki i wiązka światła się rozszerza. Zjawisko to nazywane jest dyfrakcją i
zachodzi dla wszystkich rodzajów fal.
Szczególnym przypadkiem nakładania się dwóch lub więcej Fal (superpozycji) jest
zjawisko interferencji. Warunkiem wystąpienia zjawiska interferencji fal jest ich spójność
(koherentność) tzn. niezmienność w czasie przesunięcia fazowego. Oznacza to, że
interferujące fale zachowują niezmienną w czasie odległość.
Zjawisko to przedstawimy na przykładzie interferencji dwóch fal płaskich
harmonicznych o tych samych częstościach kołowych ω, długościach fali λ i amplitudach A,
biegnących z tą samą prędkością i w tym samym kierunku. Fale te różnią się tylko fazą o kąt
φ. Równania tych fal mają postać:
k = 2π/λ: wektor falowy,
λ: długością fali.
Przesunięcie fazowe o kąt φ oznacza, że np. „szczyty” fal w układzie współrzędnych y = f(x)
są przesunięte względem siebie o odległość Δx = φ/k.
Fala płaska rozchodzi się w jednym kierunku np. wzdłuż osi X; przy rozchodzeniu się fali
harmonicznej każda cząstka ośrodka drga ruchem harmonicznym prostym.
Falę wypadkową opisuje suma powyższych równań
Fala wypadkowa posiada tę samą częstotliwość, co fale składowe oraz amplitudę
A=2Acos(φ/2) zależną od przesunięcia fazowego φ.
Jeżeli φ = 0 ,2π, 4π, mówimy wtedy, że fale spotykają się w tych samych fazach (np.
„szczyt” jednej fali spotyka się ze „szczytem” drugiej). Amplituda fali wypadkowej osiąga
wartość maksymalną A + 2A ponieważ cos (φ/2) = 1. W punkcie, w którym fale spotykają się
w tych samych fazach powstaje maksimum interferencyjne. Jeżeli φ = π, 3π, 5π … fale
spotykają się w fazach przeciwnych (tj. „szczyt” jednej fali spotyka się z „doliną” drugiej), a
amplituda a = 0 ponieważ cos (φ/2) = 0. W miejscu spotkania się tych fal powstaje minimum
interferencyjne.
Dwie spójne fale świetlne otrzymamy m.in. wtedy, gdy światło wychodząc z
punktowego źródła skierujemy na dwie wąskie szczeliny. Różnica faz między falami
powstaje z powodu różnicy dróg optycznych, jakie przebiegną te fale do punktu, w którym
nastąpi interferencja (drogą optyczną nazywamy iloczyn drogi geometrycznej i
bezwzględnego współczynnika załamania n ośrodka, w którym rozchodzi się fala; dla
powietrza n = 1).
Maksimum interferencyjne występuje dla φ = 0, 2π, 4π… oznacza że różnica dróg
przyjmuje wartość 0, λ, 2λ…,kλ gdzie k jest liczbą całkowita.
Minimum interferencyjne wystąpi wówczas gdy φ = π, 3π, 5π… czyli dla
Jeżeli różnica dróg optycznych przebytych przez dwie fale świetlne do punktu w
którym nastąpi interferencja będzie równa całkowitej wielokrotności długości fali to
otrzymamy maksimum interferencyjne:
n ∙ Δs = kλ
Jeżeli różnica dróg optycznych będzie równa nieparzystej wielokrotności połówek
długości fali, w miejscu nałożenia się fal świetlnych wystąpi minimum interferencyjne:
n ∙ Δs = (2k + 1) λ/2
Zasada pomiaru:
Pierścienie Newtona otrzymujemy, gdy światło monochromatyczne (jednobarwne) pada na
układ składający się z soczewki płasko – wypukłej S i płytki płasko – równoległej P. Między
soczewką a płytką znajduje się cienka warstwa powietrza, której grubość wzrasta stopniowo
od punktu styku ku brzegom. Światło padające prostopadle na układ soczewka – płytka ulega
częściowo odbiciu na każdej powierzchni granicznej. Promienie odbite mogą ze sobą
interferować. Pierścienie Newtona powstają w wyniku interferencji promienia odbitego od
górnej powierzchni płytki P z promieniem odbitym od sferycznej powierzchni soczewki.

Między tymi promieniami istnieje różnica dróg s  2d  (dla n=1 powietrza)
2
d- grubość warstwy powietrza od osi symetrii, λ/2- zmiana fazowa fali odbitej od płytki P
Interferencja zachodzi pomiędzy promieniami odbitymi od dolnej powierzchni
soczewki (punkt C) i od górnej powierzchni płytki płasko- równoległej (punkt B). Prążki
Interferencyjne odpowiadające jednakowej grubości warstwy powietrza będą tworzyły
współśrodkowe okręgi, na przemian jasne i ciemne: Pierścienie Newtona.
Ciemny środek oznacza, że w miejscu styku płytek występuje minimum interferencyjne.
Promienie odbite od soczewki i płytki płasko- równoległej w miejscu styku mają te same
długości drogi optycznej, ale odbicie od płytki zachodzi ze zmianą fazy o л, gdyż promień
światła odbija się od ośrodka optycznie gęstszego (ośrodek o większym współczynniku
załamania). Przy odbiciu fali od środowiska o większym współczynniku załamania, niż
współczynnik załamania środowiska, w którym fala się przemieszcza zachodzi zmiana fazy o
180 , co odpowiada różnicy dróg równej λ/2.
Porównując powyższy wzór ze wzorem na minimum: n ∙ Δs = (2k + 1) λ/2 ,



2d   (2k  1)  d  k
otrzymamy:
2
2
2
W celu ustalenia zależności między promieniami pierścieni jasnych lub ciemnych i
długością fali przeprowadzamy analizę geometryczną:
DC 2  AD  DE czyli rk2  2R - d d
wobec tego  rk2=kλR
Znając promień k-tego prążka Newtona i długość fali możemy obliczyć promień krzywizny R
soczewki płasko- wypukłej. Wartość R wyznaczamy z wykorzystaniem metody
najmniejszych kwadratów. Powyższy wzór można porównać z równaniem prostej y=ax+b
y=r2 x=k a=Rλ  R=a/λ
Obliczenia wartości parametrów a i b wykonujemy za pomocą programu „Regresja”.
Prawidłowy kształt pierścieni ulega zakłóceniu nawet przy maleńkich niedokładnościach.
Dlatego obserwacja pierścieni pozwala przeprowadzić szybką i dokładną kontrolę jakości
szlifów powierzchni płaskich i soczewek.
Zestaw pomiarowy:
Mikroskop, zestaw płasko – równoległej płytki szklanej i soczewki płasko – wypukłej, lampa
sodowa.
Światło lampy sodowej pada na soczewkę. Po odbiciu od zwierciadła ustawionego pod kątem
45 do pionu, znajdującego się wewnątrz mikroskopu, strumień światła jest kierowany
prostopadle na układ płytek. Powiększony obraz pierścieni obserwujemy w okularze
mikroskopu. Ostrość pierścieni ustawiamy za pomocą pokrętła. W okularze widoczny jest
krzyż z nici pajęczej, który możemy ustawić na dowolnym prążku, za pomocą śrub
mikrometrycznych przymocowanych do stolika mikroskopu.
Przebieg ćwiczenia:
1. Włączamy do sieci zasilacz lampy sodowej.
2. Kładziemy na stoliku mikroskopu płytkę grubości 25 mm, stroną matową do stolika
mikroskopu. Na płytkę kładziemy soczewkę tak, aby strzałka zaznaczona na jej
bocznej powierzchni była skierowana ostrzem w dół.
3. Ustawiamy lampę sodową na wprost soczewki mikroskopu.
4. Pokrętłem przesuwamy kolumnę mikroskopu tak, aby w polu widzenia ukazał się
ostry obraz pierścieni Newtona, przy czym w środku powinien być ciemny prążek.
5. Pokrętłem śrub mikrometrycznych sprowadzamy środek krzyża nici pajęczej do
pokrycia się z środkiem pierścieni.
6. Pokrętłem śruby mikrometrycznej sprowadzamy środek krzyża nici pajęczej do
pokrycia się z k-tym (k>5) prążkiem po lewej stronie, następnie po prawej odczytując
wskazania mikrometru 1 i p, 1-p będzie średnicą promienia.
7. Czynność 6 wykonujemy dla 12 różnych pierścieni.
8. Wyniki 1 i p wpisujemy do tabeli.
9. Wykorzystując komputer, wyposażony w program „Regresja” obliczamy wartości a, b
prostej y=ax+b, oraz ich odchylenia standardowe δa δb następnie przeprowadzamy
zaokrąglenie tych wartości (zgodnie z normami).
Zauważmy że wzór rk2 = kλR, jest szczególną postacią równania prostej y=ax+b;
gdzie y=r2 x=k a=Rλ => R=a/λ
Opracowanie ćwiczenia:
lp
i wpisujemy do odpowiedniej kolumny tabeli
2
2. Rysujemy prostą y=ax+b oraz nanosimy na ten wykres punkty pomiarowe
3. Wartość długości fali światła stosowanej w ćwiczeniu lampy sodowej λ=0,589*10-6
4. Obliczamy wartość R (wykorzystując zaokrągloną wartość a) ze wzoru R=a/λ
1. Obliczamy wartości rk 
Rachunek błędu:
1. Obliczamy błąd standardowy δR
R 
R
1
a a
a  a 
a

 a
ostatecznie:
R  R
a
a
2. Zaokrąglamy wartości R i δR (zgodnie z normami) i wpisujemy do tabeli.
3. Obliczamy błąd względny.
Tabela pomiarowa:
Numer
pierścienia
k
Wskazania mikrometru
Na lewo l
[10-3m]
Na prawo p
[10-3m]
lp
2
[10-3m]
rk 
rk2
[10-6m]
λ
[10-6m]
R
[m]