Liczby nieujemne to liczby dodatnie i zero

, które mają tylko dwa różne dzielniki.
czby w postaci
dziesiętnej.
nktu odpowiadającego tej liczbie na osi liczbowej.
czba
dodatnia.
współczynnika liczbowego.
-b) = a – 2ab + b kwadrat różnicy dwóch wyrażeń
(a+b)(a-b) = a – b iloczyn sumy przez różnice dwóch wyrażeń.
- wyłączanie wspólnego czynnika przed nawias. - stosowanie wzorów skróconego
mnożenia. - grupowanie wyrazów.
zb w miejsce liter w wyrażeniu i wykonaniu wskazanych
działań.
tylko jedna niewiadoma to o takich równaniach mówimy, że są to równania pierwszego stopnia z jedną
niewiadomą.
akiej liczby rzeczywistej, która spełnia to równanie.
a ma tę samą własność, że iloczyn wyrazów skrajnych równy jest iloczynowi wyrazów
środkowych.
ym
każdemu elementowi zbioru A jest przyporządkowany dokładnie jeden element zbioru B.
aka w której ze wzrostem wartości argumentów x, maleją wartości funkcji y.
st ta sama wartość funkcji y.
źnie to układ dwóch prostych prostopadłych zwanych osiami współrzędnych, oś pionowa
y – oś rzędnych, oś pozioma x – oś odciętych.
pierwszego stopnia, którego nie spełnia żadna para liczby, nazywamy układem sprzecznym.
wiadomymi jest prosta.
tych są
rozwiązaniem tego układu równań.
. Układ ten ma nieskończenie wiele rozwiązań.
zbiór
pusty.
reślająca położenie punktu względem osi współrzędnych
adanie opinii publicznej na podstawie przeprowadzonego wywiadu.
najmniejszej do największej.
przekątne
- ramiona są równej długości , - przekątne są równej długości, - kąty przy podstawach są równej miary, - mają
jedną oś symetrii.
- jedno ramię jest jednocześnie wysokością trapezu.
ją dwie pary boków równoległych
- boki równoległe są równej długości, - przeciwległe kąty są równej miary, - przekątne dzielą się na połowy.
- wysokości są równe - ma dwie osie symetrii przekątne: - są prostopadłe, - zawierają się w dwusiecznych kątów wewnętrznych, zawierają się w osiach symetrii rombu, - przecinają się w środku okręgu wpisanego w romb.
- przekątne są równej długości, - symetralne boków równoległych są osiami symetrii prostokąta, - punkt przecięcia przekątnych
jest środkiem okręgu opisanego na prostokącie.
wszystkie boki równej długości
Kwadrat - ma cztery osie symetrii przekątne: - są prostopadłe i równej długości, - zawierają się w osiach symetrii, - zawierają się w
dwusiecznych kątów wewnętrznych, - przecinają się we wspólnym punkcie, w środku okręgów opisanego na kwadracie i wpisanego
wkwadrat.
ąt można podzielić na dwa trójkąty, a zatem suma miar kątów wewnętrznych czworokąta jest równa 360.
iar kątów przyległych są równe 180.
– 2) 180
ąta foremnego możemy wyznaczyć ze wzoru: , gdzie n jest liczbą boków wielokąta
prostokąta:
Wzór na pole koła:
długości przyprostokątnych tego trójkąta.
ie kwadrat długości najdłuższego boku jest równy sumie kwadratów
długości pozostałych boków trójkąta, to ten trójkąt jest prostokątny.
lesa : Jeżeli ramiona kąta przecięte są prostymi równoległymi, to stosunek długości którychkolwiek dwóch
odcinkówutworzonych na jednym ramieniu jest równy stosunkowi długości odpowiednich odcinków utworzonych na drugim ramieniu.
twierdzenia Talesa: Jeżeli proste przecinające ramiona kąta wyznaczają na jednym ramieniu
odcinkiproporcjonalne do odpowiednich odcinków utworzonych na drugim ramieniu, to te proste są równoległe.
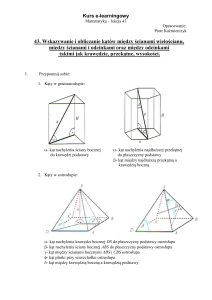
- podstawy są przystającymi wielokątami, - podstawy leżą w płaszczyznach równoległych, - krawędzie boczne są
równoległe, - ściany boczne są równoległobokami.
mny, nazywamy graniastosłupem prawidłowym.
upy: - podstawa jest wielokątem, - ma jedną podstawę, - ściany boczne są trójkątami o wspólnym wierzchołku, który nazywamy
wierzchołkiem podstawy. - krawędzie wychodzące z wierzchołka ostrosłupa na płaszczyznę podstawy to spodek wysokości tego ostrosłupa,odcinek łączący wierzchołek ostrosłupa z jego spodkiem wysokości to wysokość ostrosłupa.
rego podstawą jest wielokąt foremny, a ściany boczne są przystającymi trójkątami równoramiennymi, nazywamy
ostrosłupem prawidłowym.
lnej
krawędzi, a ramiona są do niej prostopadłe i jedno ramię leży na ścianie bocznej, a drugie na podstawie.
ocznej graniastosłupa prostego:
y przez obrót prostokąta o 360 dokoła prostej zawierającej jeden z jego boków.
które są przystającymi kołami
ileżą względem siebie równolegle.
em osiowym walca jest prostokąt.
prostokątny dokoła prostej zawierającej jedną z przyprostokątnych o kąt 360 .
0 dokoła prostej zawierającej średnicę.
na pole powierzchni bocznej stożka:
Wzór na objętość walca:
jące to takie, które po nałożeniu na siebie pokrywają się.
o kąt wypukły, którego wierzchołek jest punktem okręgu koła, a ramiona zawierają cięciwy tego koła.
zchołki wielokąta.
do figury.
tosłupa to dwie równoległe ściany tego graniastosłupa, na których leżą wszystkie wierzchołki graniastosłupa.
ączący dowolne dwa niekolejne wierzchołki wielokąta.
Symetralna odcinka to prosta prostopadła do odcinka przechodzącego przez jego środek.
ca przez środek okręgu.
należą do
figury.
go.
k trójkąta, prostopadłej do przeciwległego boku, liczony od
wierzchołka do przecięcia się prostej z przeciwległym bokiem lub jego przedłużeniem.