Wykład z fizyki – Piotr Posmykiewicz
1
Wykład 31
Cząsteczki i ciała stałe.
Większość atomów jest połączona między sobą tworząc cząsteczki lub ciała stałe. Cząsteczki
mogą istnieć jako odrębne całości w gazach na przykład O2, N2 lub mogą łączyć się tworząc ciecze
lub ciała stałe. Cząsteczka jest najmniejszą częścią składową substancji, która zachowuje swoje
własności chemiczne.
31.1 Wiązania cząsteczkowe.
Istnieją dwa skrajne spojrzenia na cząsteczkę. Weźmy pod uwagę na przykład cząsteczkę H2.
Możemy ją traktować jako dwa atomy połączone razem, lub jako układ kwantowo – mechaniczny
składający się z dwu protonów i dwu elektronów. Drugie podejście jest bardziej owocne w tym
wypadku, ponieważ żaden z elektronów w H2 nie może być przypisany do jednego czy drugiego
protonu. Zamiast tego, mamy funkcję falową, która rozciąga się na całą przestrzeń zajmowaną przez
cząsteczkę. Jednak dla bardziej skomplikowanych cząsteczek, pożyteczne jest pośrednie podejście.
Na przykład, cząsteczka azotu składa się z 14 protonów i 14 elektronów, jednak tylko dwa elektrony
uczestniczą w wiązaniu. Dlatego też możemy traktować taką cząsteczkę jako składającą się z dwu
jonów N+ i dwóch elektronów, które należą do cząsteczki jako całości. Cząsteczkowe funkcje falowe
tych elektronów nazywają się orbitalami cząsteczkowymi. W szeregu przypadkach te funkcje
falowe mogą być zbudowane na bazie kombinacji atomowych funkcji falowych.
Podstawowymi typami wiązań odpowiedzialnymi za tworzenie się cząsteczek są wiązania jonowe
i kowalencyjne. Innymi rodzajami wiązań, które odgrywają dużą rolę w przypadku wiązań w
cieczach i ciałach stałych są wiązania van der Waalsa, wiązania metaliczne i wiązania wodorowe. W
wielu przypadkach mamy do czynienia z mieszaniną tych mechanizmów.
Wiązania jonowe.
Najprostszym typem wiązań jest wiązanie jonowe, które występuje w solach takich jak chlorek
sodu (NaCl). Atom sodu posiada jeden elektron 3e na zewnątrz stabilnego wnętrza. Energia
potrzebna do usunięcia tego elektronu wynosi 5,14eV i jest to energia jonizacji. Po usunięciu tego
elektronu otrzymujemy dodatnio naładowany jon o sferycznej symetrii, z zamkniętymi powłokami.
Chlor, z drugiej strony, posiada o jeden elektron za mało do zamknięcia powłoki. Energia jaka jest
uwalniana podczas przyłączenia przez atom elektronu nazywa się jego powinowactwem
Wykład z fizyki – Piotr Posmykiewicz
2
elektronowym i w tym przypadku wynosi 3,62eV. Przyłączenie jednego elektronu przez chlor
prowadzi do powstania ujemnego jonu, o sferycznej symetrii i zapełnionej ostatniej powłoce. Tak
więc utworzenie układu Na+ i Cl- wymaga tylko dostarczenia energii 5,14eV – 3,62eV = 1,52eV.
Elektrostatyczna energia potencjalna dwu jonów znajdujących się w odległości r od siebie jest równa
–ke2/r. Kiedy odległość między jonami jest mniejsza niż 0,95nm, wtedy ujemna energia potencjalna
przyciągania jest większa niż energia 1,52eV potrzebna do utworzenia jonów. Tak więc, dla
odległości mniejszej niż 0,95eV dla atomu sodu wygodniejszym energetycznie (oznacza to, że
całkowita energia układu zmaleje) jest utworzenie NaCl poprzez oddanie jednego elektronu.
Ponieważ przyciąganie elektrostatyczne zwiększa się wraz z przybliżaniem jonów, to
wydawałoby się, że stan równowagi nie istnieje. Jednak kiedy odległość staje się bardzo mała, to
pojawia się bardzo silne odpychanie posiadające naturę kwantową, a które związane jest z zakazem
Pauliego. Odpychanie wynikające z zakazu Pauliego jest charakterystyczne dla wszystkich atomów
w cząsteczkach (oprócz H2), dla wszystkich mechanizmów wiązań. Jakościowo można to zrozumieć
następująco. Kiedy dwa jony znajdują się daleko od siebie, wtedy funkcje falowe elektronów z obu
jonów nie zachodzą na siebie. Możemy wtedy rozróżnić elektrony w jonie, do którego należą.
Oznacza to, że elektrony w tych dwóch jonach mogą mieć te same liczby kwantowe, ponieważ
zajmują różne obszary przestrzeni. Jednak, gdy odległość między jonami zmniejsza się, funkcje
falowe elektronów powłok zaczynają na siebie zachodzić, czyli że elektrony z tymi samymi liczbami
kwantowymi zaczynają zajmować ten sam obszar powierzchni. Z powodu zakazu Pauliego niektóre
elektrony muszą przejść do wyższego kwantowego stanu energetycznego. Jednak do tego potrzebna
jest dodatkowa energia. Ten wzrost energii kiedy elektrony zbliżają się do siebie jest równoważny
siłom odpychania jonów. Nie jest
to
proces
gwałtowny.
energetyczne
Stany
elektronów
zmieniają się stopniowo wraz z
przybliżaniem
się
jonów.
Rysunek 31.1 przedstawia wykres
energii potencjalnej dwu jonów
+
Energia dysocjacji
4,27eV
Rysunek 31.1
-
Na i Cl w funkcji wzajemnej
odległości. Energia jest najniższa w punkcie równowagi około 0,236nm. Energia, która jest
potrzebna do rozdzielenia jonów na dwa oddzielne atomy nazywa się energią dysocjacji, która w
przypadku NaCl wynosi 4,27eV.
Równowagowa odległość 0,236nm jest prawidłowa jeżeli mamy cząsteczki dwuatomowe NaCl w
postaci gazowej. Normalnie NaCl istnieje w postaci sześciennej struktury krystalicznej z jonami Na+
i Cl- przemiennie w rogach sześcianu. Odległość między jonami w krysztale nieco większa i wynosi
Wykład z fizyki – Piotr Posmykiewicz
3
0,28nm. Z powodu obecności sąsiednich jonów posiadających przeciwne ładunki, energia
elektrostatyczna przypadająca na jedną parę jonów jest mniejsza kiedy jony tworzą strukturę
krystaliczną.
Wiązania kowalencyjne.
Zupełnie inny rodzaj wiązań odpowiada za połączenia identycznych lub podobnych atomów
takich jak gazowy wodór (H2), czy azot (N2) lub tlenek węgla (CO). Wiązania te nazywają się
kowalencyjnymi. Jeżeli policzymy energię, która jest potrzebna do utworzenia jonów H+ i Hpoprzez przeniesienie z jednego atomu do drugiego elektronu i następnie dodamy tę energię do
potencjalnej energii elektrostatycznej, to stwierdzimy, że nie istnieje taka odległość między jonami
dla której całkowita energia byłaby ujemna. W związku z tym wiązanie nie może być jonowe.
Zamiast tego wzajemne przyciąganie się dwóch atomów wodoru ma całkowicie kwantowomechaniczny charakter. Zmniejszanie się energii, kiedy dwa atomy wodoru są zbliżane do siebie jest
spowodowane tym, że dwa elektrony są dzielone przez oba atomy. Jest to ściśle związane z
własnościami symetrii funkcji falowych obu elektronów.
Możemy przyjrzeć się głębiej wiązaniu kowalentnemu poprzez rozpatrzenie prostego
jednowymiarowego kwantowo-mechanicznego zagadnienia dla
dwu prostokątnych studni potencjału. Najpierw rozważmy
elektron, który jest z jednakowym prawdopodobieństwem w
każdej ze studni. Ponieważ studnie są identyczne, to rozkład
prawdopodobieństwa, który jest proporcjonalny do ψ2 musi
być symetryczny względem punktu pośrodku między studniami.
Wtedy ψ również musi być symetryczna lub antysymetryczna
względem studni. Te dwie możliwości dla stanu podstawowego
pokazane są na rysunku 31.2a w przypadku studni oddalonych
od siebie i na rysunku 31.2b kiedy studnie znajdują się bliżej
siebie. Ważną cechą na rysunku 31b jest fakt, że w rejonie
między studniami symetryczna funkcja falowa jest duża, a
antysymetryczna funkcja falowa jest mała.
Rozważmy teraz sytuację kiedy dodamy drugi elektron do obu
studni potencjału. Na gruncie mechaniki kwantowej pokazuje
się, że funkcje falowe cząstek, które podlegają zakazowi
Pauliego muszą być antysymetryczne ze względu na zamianę
cząstek. Tak więc całkowita funkcja falowa tych dwu
elektronów musi być antysymetryczna ze względu na zamianę
elektronów. Zwróćmy uwagę, że zamiana elektronów w
Rysunek 31.2
Wykład z fizyki – Piotr Posmykiewicz
4
studniach jest równoważna zamianie studni. Całkowita funkcja falowa dwu elektronów może być
zapisana jako
iloczyn części przestrzennej i części spinowej. Zatem antysymetryczna funkcja
falowa może być iloczynem symetrycznej części przestrzennej i antysymetrycznej części spinowej
lub symetrycznej części spinowej i antysymetrycznej części przestrzennej.
Aby zrozumieć symetrię całej funkcji falowej musimy zrozumieć symetrię części spinowej funkcji
1
falowej. Spin pojedynczego elektronu może przybierać dwie wartości liczby spinowej: 𝑚𝑠 = + 2,
1
który nazwijmy spin do góry i 𝑚𝑠 = − 2, który nazwijmy spin na dół. Użyjmy strzałek w celu
oznaczenia spinowej funkcji pojedynczego elektronu: ↑1 lub
↑2 dla elektronu pierwszego lub
drugiego ze spinem do góry, i ↓1 lub ↓2 dla elektronu 1 lub 2 ze spinem do dołu. Całkowita liczba
spinowa dla dwu elektronów może być równa S = 1 z mS = +1 lub mS = -1, lub S =0 z mS = 0.
Oznaczmy przez 𝜙𝑆,𝑚 𝑆 funkcję falową dla dwu elektronów. Stan spinowy ϕ1,+1, odpowiadający S = 1
i mS = +1, można zapisać:
𝜙1,+1 =↑1 ↑2 ,
S = 1, mS = +1
31.1
S = 1, mS = -1
31.2
Podobnie dla stanu spinowego S = 1 i mS = -1:
𝜙1,−1 =↓1 ↓2 ,
Zwróćmy uwagę, że oba te stany są symetryczne ze względu na zamianę elektronów. Stan spinowy
odpowiadający S = 1 i mS = 0 nie jest tak oczywisty. Okazuje się, że jest on proporcjonalny do
𝜙1,0 =↑1 ↓2 +↑2 ↓1 ,
S = 1, mS = 0
31.3
Ten stan jest również symetryczny ze względu na zamianę elektronów. Stan spinowy
odpowiadający dwóm elektronom o antyrównoległych spinach (S = 0) ma postać
𝜙1,0 =↑1 ↓2 −↑2 ↓1 ,
S = 1, mS = 0
31.4
Ten stan spinowy jest antysymetryczny względem zamiany elektronów.
Otrzymujemy zatem ważny wniosek, który mówi, że spinowa część funkcji falowej jest
symetryczna dla spinów równoległych (S = 1) i antysymetryczna dla spinów antyrównoległych (S =
0). Ponieważ całkowita funkcja falowa jest iloczynem przestrzennej i spinowej części, to
otrzymujemy następujący ważny wniosek:
Aby całkowita funkcja falowa dwu elektronów była antysymetryczna, część przestrzenna musi
być antysymetryczna dla spinów równoległych (S = 1) i symetryczna dla spinów
antyrównoległych (S = 0).
Możemy teraz rozpatrzeć przypadek dwóch atomów wodoru. Rysunek 31.3a przedstawia
przestrzennie symetryczną funkcję ψS i przestrzennie antysymetryczną funkcję ψA dla dwu atomów
Wykład z fizyki – Piotr Posmykiewicz
5
wodoru, które znajdują się daleko od siebie. Rysunek 31.3b przedstawia te same funkcje w
przypadku, gdy znajdują
się
blisko
siebie.
Na
rysunku 31.3c pokazane
są kwadraty tych funkcji.
Zwróćmy
uwagę,
że
rozkład
prawdopodobieństwa
ψ2 w obszarze między
Rysunek 31.3
protonami jest duży dla symetrycznych funkcji falowych i mały dla funkcji falowych
antysymetrycznych. Tak więc, gdy część przestrzenna funkcji falowej jest symetryczna (S = 0),
wtedy elektrony znajdują się często między protonami. Ujemnie naładowana chmura elektronowa
reprezentująca te dwa elektrony jest skoncentrowana między w przestrzeni między protonami, jak
pokazane jest to na rysunku 31.3c i protony są połączone przez ujemnie naładowaną chmurę.
Odwrotnie, w przypadku gdy część przestrzenna funkcji falowej jest antysymetryczna (S = 1),
elektrony spędzają mało czasu między protonami i atomy te nie tworzą połączenia wiążącego je w
cząsteczkę. Widać (dolna część rysunku 31.3c), że chmura elektronowa nie jest umiejscowiona
między protonami.
Całkowita
elektrostatyczna
energia
potencjalna dla cząsteczki H2 składa się z
dodatniej energii odpychania dwóch elektronów
i
ujemnej
energii
przyciągania
każdego
elektronu przez każdy z protonów. Rysunek 31.4
przedstawia elektrostatyczną energię potencjalną
dla dwu atomów wodoru w funkcji odległości
r, nm
między nimi dla przypadku, gdy przestrzenna
część funkcji falowej elektronu jest symetryczna
(US) i dla przypadku, gdy jest antysymetryczna
(UA). Widzimy, że w przypadku symetrycznego
Rysunek 31.4
stanu energia potencjalna jest podobna jak dla
wiązań jonowych. Równowagowy odstęp między atomami, w tym wypadku, wynosi r0 = 0,074nm, a
energia wiązania 4,52eV. Dla stanu antysymetrycznego energia potencjalna nigdy nie jest ujemna i,
w związku z tym, nie istnieje wiązanie.
Możemy teraz zrozumieć dlaczego atomy wodoru nie tworzą cząsteczki H3. Jeżeli trzeci atom
wodoru znajdzie się w pobliży cząsteczki H2, to trzeci elektron nie może znaleźć się w stanie 1s i
Wykład z fizyki – Piotr Posmykiewicz
6
mieć spin antyrównoległy do spinu obu elektronów. Jeżeli elektron ten znajduje w
antysymetrycznym przestrzennym stanie względem jednego z elektronów, wtedy odpychanie tego
atomu jest większe niż przyciąganie drugiego. Ponieważ wszystkie te trzy atomy znajdowały by się
blisko siebie wtedy, w efekcie, trzeci elektron byłby zmuszony do przejścia do wyższego stan
energetycznego z powodu zasady Pauliego. Wiązanie między dwoma atomami wodoru nazywa się
wiązaniem nasyconym, ponieważ nie ma miejsca dla jeszcze jednego elektronu. Te dwa dzielone
przez atomu elektrony zapełniają, w istocie, 1s stany w obu atomach.
Można również zrozumieć dlaczego dwa atomy helu nie łączą się aby stworzyć cząsteczkę He 2.
W tym wypadku nie ma elektronów walencyjnych, które mogły by być dzielone między atomy helu.
Elektrony w zamkniętych powłokach są zmuszane do przejścia na wyższy poziom energetyczny,
jeżeli dwa atomy są zbliżane do siebie. W niskich temperaturach lub przy wysokim ciśnieniu atomy
helu łączą się razem dzięki siłom van der Waalsa, o których będzie mowa dalej. Wiązanie jest
jednak tak słabe, że przy ciśnieniu atmosferycznym hel wrze w temperaturze 4K i przechodzi nigdy
w stan stały, chyba że ciśnienie wynosi 20atm.
Kiedy łączą się dwa identyczne atomy, takie jak O2 lub N2, to wiązanie jest czysto kowalentne.
Jednak wiązanie dwu niejednakowych atomów jest często mieszaniną wiązania kowalentnego i
jonowego.
Nawet
NaCl
elektron
oddany przez
sód
atomowi chloru
posiada
pewne
prawdopodobieństwo znalezienia się w pobliżu atomu sodu, ponieważ jego funkcja falowa nie
maleje natychmiast do zera. Tak więc, elektron ten jest częściowo dzielony w wiązaniu
kowalentnym, chociaż ten rodzaj wiązania ma mały udział w całkowitym wiązaniu, które głównie
ma charakter jonowy.
Inne typy wiązań.
Wiązania van der Waalsa. Dowolne dwie oddzielne cząsteczki są przyciągane do siebie przez
siły elektrostatyczne zwane siłami van der Waalsa. Podobnie będą się przyciągać dowolne dwa
atomy, które nie tworzą wiązania jonowego, czy kowalentnego. Siły te zwane siłami van der
Waalsa są znacznie słabsze od sił, o których była wcześniej mowa. W wysokich temperaturach siły
te nie są w stanie przezwyciężyć zwykłego wzbudzenia atomów czy cząsteczek, jednak w
odpowiednio niższych temperaturach wzbudzenie termiczne staje się pomijalne i siły van der Waalsa
powodują, że praktycznie wszystkie substancje kondensują w
ciecze, a następnie w ciała stałe. Siły van der Waalsa powstają
pod
wpływem
tworzenia
się
chwilowych
momentów
elektrycznych cząsteczek.
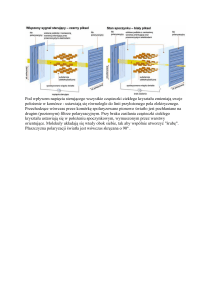
Rysunek 31.5 przedstawia dwie polarne cząsteczki –
cząsteczki z trwałym elektrycznym momentem dipolowym,
takie jak H2O, mogą łączyć się. Pole elektryczne wytworzone
Rysunek 31.5
Wykład z fizyki – Piotr Posmykiewicz
7
przez moment dipolowy jednej cząsteczki powoduje zorientowanie innej cząsteczki w ten sposób, że
obie cząsteczki się przyciągają. Niepolarne cząsteczki również przyciągają inne niepolarne
cząsteczki poprzez siły van der Waalsa. Pomimo tego, że średni moment elektryczny cząsteczek
niepolarnych wynosi zero, to posiadają one chwilowy moment dipolowy, który jest różny od zera i
jest spowodowany fluktuacjami w położeniach ładunków. Kiedy dwie niepolarne cząsteczki są obok
siebie , wtedy ich chwilowe momenty dipolowe starają się być uzgodnione w czasie, co prowadzi do
ich przyciągania. Przedstawia to rysunek 31.6.
Wiązania wodorowe. Innym bardzo ważnym mechanizmem połączeń są wiązania wodorowe.,
które tworzą się poprzez dzielenie wspólnego protonu pomiędzy dwa atomy, często między dwa
atomy tlenu. Dzielenie protonu jest podobne do dzielenia elektronu w wiązaniach kowalentnych.
Dzieje się tak dlatego, że proton posiada małą masę i nie posiada wewnętrznych powłok
elektronowych. Wiązania wodorowe często wiążą grupę cząsteczek i są odpowiedzialne za
połączenia międzycząsteczkowe, które umożliwiają ogromnym biologicznym cząsteczką lub
polimerom utrzymanie swojego kształtu. Dobrze znana spiralna struktura DNA powstaje dzięki
wiązaniom wodorowym.
Wiązania metaliczne. W metalu dwa atomy
nie łączą się poprzez wymianę lub dzielenie
elektronu.
Zamiast
tego
każdy walencyjny
elektron jest wspólny dla wielu jonów. W
rezultacie połączenia są rozprzestrzenione po
całym metalu. Metal można wyobrazić sobie jako
siatkę dodatnich jonów utrzymywanych razem
przez „gaz”, w zasadzie, swobodnych elektronów
poruszających się w całej objętości metalu. W
podejściu kwantowo – mechanicznym te wolne
Rysunek 31.6
elektrony tworzą chmurę elektronową zespalającą
dodatnie jony. W takim podejściu, wiązania
metaliczne przypominają do pewnego stopnia wiązania kowalentne.
31.2 Poziomy energetyczne i widma cząsteczek dwuatomowych.
Podobnie
jak
atomy
cząsteczki
często
wypromieniowują
energię
w
postaci
fali
elektromagnetycznej podczas przejścia ze stanu wzbudzonego do niższego stanu. I odwrotnie
cząsteczki mogą absorbować energię i przechodzić wyższy stan wzbudzenia. W związku z tym
badanie widm emisyjnych i absorpcyjnych cząsteczek dostarcza informacji o
stanach
Wykład z fizyki – Piotr Posmykiewicz
8
energetycznych cząsteczek. Dla prostoty ograniczymy się tylko do analizy cząsteczek
dwuatomowych.
Energię cząsteczek może być dla wygody podzielona na trzy części: elektronową – wywołaną
wzbudzeniem elektronów w cząsteczce, oscylacyjną – wywołaną drganiami atomów w cząsteczce i
rotacyjną – wywołaną obrotem cząsteczki wokół swojego środka masy. Energie wywołane
wzbudzeniem elektronów cząsteczki są rzędu 1eV, podobnie jak wzbudzenie atomu. Energie
rotacyjne i oscylacyjne są znacznie mniejsze.
Rotacyjne poziomy energetyczne.
Rysunek 31.7 przedstawia prosty schematyczny model cząsteczki
dwuatomowej składający się z masy m1 i m2 w odległości r od siebie
i obracających się wokół ich wspólnego środka masy. W podejściu
klasycznym energia kinetyczna ruchu obrotowego wynosi
1
𝐸 = 2 𝐼𝜔2
31.5
gdzie I jest momentem bezwładności, a ω jest prędkością kątową.
Podstawiając moment pędu L = Iω, 31.5 możemy przepisać w postaci:
𝐸=
𝐼𝜔 2
2𝐼
𝐿2
= 2𝐼
Rysunek 31.7
31.6
Rozwiązanie równania Schrödingera dla ruchu obrotowego prowadzi do skwantowania momentu
pędu o wartościach
𝐿2 = ℓ ℓ + 1 ℏ2 ,
ℓ = 0, 1, 2, …
31.7
gdzie 𝓵 jest rotacyjną liczbą kwantową. Jest to ten sam warunek kwantowania momentu pędu, który
istnieje dla orbitalnego momentu pędu w atomie. Zwróćmy jednak uwagę, że tutaj L w równaniu 31.6
odnosi się do momentu pędu całej cząsteczki obracającej się wokół środka masy. Poziomy energetyczne
otrzymamy podstawiając 31.7 do 31.6:
𝐄=
𝓵 𝓵+𝟏 ℏ𝟐
𝟐𝐈
= 𝓵 𝓵 + 𝟏 𝐄𝟎𝐫 ,
𝓵 = 𝟎, 𝟏, 𝟐, …
31.8
Rotacyjne poziomy energii.
gdzie E0r jest charakterystyczną energią rotacyjną danej cząsteczki, która jest odwrotnie
proporcjonalna do momentu bezwładności:
𝐸0𝑟 =
ℏ2
2𝐼
Charakterystyczna energia rotacyjna.
31.9
Wykład z fizyki – Piotr Posmykiewicz
9
Mierząc energię rotacyjną cząsteczki na podstawie widma rotacyjnego można określić moment
bezwładności cząsteczki, który z kolei można użyć do znalezienia odległości między atomami w
cząsteczce. Moment bezwładności względem osi przechodzącej przez środek masy dwuatomowej
cząsteczki (Rysunek 31.7) wynosi
𝐼 = 𝑚1 𝑟12 + 𝑚2 𝑟22
Podstawiając m1r1 = m2r2, co wynika z przyjęcia położenia początku układu odniesienia w środku
masy i r1 + r2 = r0 otrzymujemy:
𝐼 = 𝜇𝑟02
31.10
gdzie μ nazywa się masą zredukowaną:
𝐦 𝐦
𝛍 = 𝐦 𝟏+𝐦𝟐
𝟏
31.11
𝟐
Definicja – masa zredukowana.
1
Jeżeli masy są równe tak jak np. w O2 lub H2 wtedy masa zredukowana jest równa 𝜇 = 2 𝑚
i
1
𝐼 = 2 𝑚𝑟02
31.12
Wygodną jednostką masy w zastosowaniach do mas atomów i cząsteczek jest atomowa
jednostka masy u, zdefiniowana jako jedna dwunasta masy neutralnego atomu węgla (12C). Dlatego
też masa atomu w jednostkach u jest równa liczbowo masie molowej atomu w gramach. Jest ona
równa:
1𝑔
10 −3 𝑘𝑔
1𝑢 = 𝑁 = 6,0221 ∙10 23 = 1,6606 ∙ 10−27 𝑘𝑔
31.13
𝐴
Przykład 1.
Oszacuj charakterystyczną energię rotacyjną cząsteczki O2 przyjmując, że odległość między
atomami wynosi 0,1nm.
1
1. Wzór określający moment bezwładności:
𝐼 = 𝜇𝑟02 = 2 𝑚𝑟02
2. Podstawiając do 31.9:
𝐸0𝑟 = 𝑚 𝑟 2
ℏ2
0
ℏ2
𝐸0𝑟 = 𝑚 𝑟 2 =
3. Podstawiając m = 16u dla tlenu:
0
1,05∙10 −34 𝐽 ∙𝑠
2
16𝑢 10 −10 𝑚 2
=
= 2,59 ∙ 10−4 𝑒𝑉
Z przykładu powyżej widzimy, że rotacyjne poziomy energii są o kilka rzędów mniejsze od
poziomów wzbudzenia elektronu, które są rzędu 1eV i więcej. Przejściom między poziomami
rotacyjnymi
towarzyszą
fotony
o
częstościach
z
obszaru
mikrofalowego
widma
elektromagnetycznego. Energie rotacyjne są również mniejsze od typowych energii termicznych kT
Wykład z fizyki – Piotr Posmykiewicz
10
w zwykłych temperaturach. Dla T = 300K na przykład kT jest około 2,6 ∙ 10−2 𝑒𝑉 . W rezultacie w
zwykłych temperaturach cząsteczki mogą być łatwo wzbudzone na poziomy rotacyjne poprzez
zderzenia z innymi cząsteczkami.
Oscylacyjne poziomy energetyczne.
Skwantowanie energii w drganiach prostego oscylatora harmonicznego było jednym z pierwszych
rozwiązań podanego przez Schrődingera równania falowego. Wartości własne miały postać:
1
𝐸𝜈 = 𝜈 + 2 𝑓,
𝜈 = 0, 1, 2, …
31.14
gdzie f jest częstością oscylatora, a ν jest oscylacyjną liczbą kwantową. Interesującym wnioskiem
wypływającym z tego rozwiązania jest fakt, że poziomy energetyczne są równo oddalone od siebie o
hf. Częstości drgań dwuatomowych cząsteczek można powiązać z siłą wywieraną na jeden atom
przez drugi atom. Wyobraźmy sobie dwie masy m1 i m2 połączone sprężynką o współczynniku
sprężystości K. W takim przypadku (patrz wykład o drganiach) częstość wynosi:
1
𝑓 = 2𝜋
𝐾
31.15
𝜇
gdzie μ jest dane równaniem 31.1. W rezultacie współczynnik K dla dwuatomowej cząsteczki
można zmierzyć poprzez pomiar częstości drgań cząstki.
Zasada wyboru dla drgań wymaga, aby ν zmieniało się o ±1, w związku z tym foton emitowany
takich przejściach ma energię hf i co za tym idzie częstość f taką samą jak częstość drgań.
Typowa zmierzona częstość dla przejść między poziomami oscylacyjnymi wynosi 5 ∙ 1013 𝐻𝑧, co
daje
𝐸 ≈ 𝑓 = 4,14 ∙ 10−15 𝑒𝑉 ∙ 𝑠 5 ∙ 1013 𝑠 −1 = 0,2𝑒𝑉
Typowa energia oscylacji cząsteczki O2 jest około 1000 razy większa od typowej energii rotacyjnej
E0r tej cząsteczki i około 8 razy większa niż typowa energia ruchu cieplnego kT 0,026eV dla T =
300K. W rezultacie oscylacyjne poziomy energetyczne nie mogą być wzbudzane poprzez zderzenia
cieple w temperaturach pokojowych.
Widma emisyjne.
Rysunek 31.8 ilustruje
schematycznie
Poziom podstawowy
wybrane
oscylacyjne i rotacyjne
poziomy
Energia
Poziom wzbudzony
energetyczne
dwuatomowej cząsteczki.
Poziomy oscylacyjne są
Poziomy
scharakteryzowane przez
rotacyjne
Rysunek 31.8
Wykład z fizyki – Piotr Posmykiewicz
11
liczbę kwantową ν, a
poziomy rotacyjne przez
𝓵.
liczbę
Odległość
między
niższymi
poziomami
oscylacyjnymi
jest
zawsze taka sama i równa
Wyższy
ΔE = hf. Dla wyższych
poziom
elektronowy
poziomów oscylacyjnych
przybliżenie, że drgania
Niższy
poziom
są czysto harmoniczne nie
jest
prawdziwe
odległości
i
między
poziomami
nie
dokładnie
Zwróćmy
elektronowy
są
równe.
uwagę,
krzywe
że
energii
potencjalnej
reprezentujące
siły
Rysunek 31.9
między dwoma atomami
w cząsteczce nie mają dokładnie takiego samego kształtu w przypadku stanu podstawowego i
wzbudzonego elektronów. To powoduje, że podstawowa częstość oscylacji f różni się dla różnych
stanów elektronowych. Dla przejść między oscylacyjnymi stanami różnych stanów elektronowych
reguła wyboru Δν = ±1 nie obowiązuje. Takie przejścia powodują emisję fotonów o długości fali w
pobliżu widma widzialnego, dlatego też widmo emisyjne cząsteczki dla przejść elektronowych jest
czasami zwane widmem optycznym.
Odległości między poziomami rotacyjnymi wzrastają wraz ze wzrostem ℓ. Ponieważ energie
rotacyjne są znacznie mniejsze od oscylacyjnych, czy elektronowych poziomów wzbudzenia w
cząsteczce, to rotacje cząsteczki przejawiają się widmie optycznym jako wyraźnie rozszczepione
linie spektralne. Jeżeli rozdzielczość nie jest dostateczna, to widmo wydaje się pasmowym jak to jest
pokazane na rysunku 31.9a. Po dokładnym przyjrzeniu się tym pasmom, widać, że posiadają one
strukturę dyskretną spowodowaną rotacyjnymi poziomami energii, co zostało pokazane w
powiększeniu na rysunku 31.9b.
Widma absorpcyjne.
Wykład z fizyki – Piotr Posmykiewicz
Większość
12
analiz
spektroskopowych
Energia
cząsteczek wykonywana jest przy użyciu
technik wykorzystujących widma absorpcyjne
w podczerwieni. W widmach tych wzbudzane
są tylko poziomy rotacyjne i oscylacyjne
podstawowego
stanu
elektronowego.
W
temperaturach pokojowych energie oscylacyjne
(cząsteczki w większości znajdują się w stanie
podstawowym o ν = 0, co odpowiada energii E0
1
= 2 𝑓), jakie posiadają cząsteczki, są znacząco
większe niż energia cieplna kT. Przejście z ν =
0 do ν =1 jest przejściem dominującym
przejściem absorpcyjnym. Energie rotacyjne
jednak są zdecydowanie mniejsze niż kT. Jeżeli
Rysunek 31.10
początkowo cząsteczka znajduje się w stanie
oscylacyjnym scharakteryzowanym przez ν = 0 i stanie rotacyjnym scharakteryzowanym przez ℓ, to
jej energia początkowa wynosi
1
𝐸ℓ = 2 𝑓 + ℓ ℓ + 1 𝐸0𝑟
31.16
gdzie E0r dane jest równaniem 31.9. Z tego stanu dozwolone są poprzez reguły wyboru dwa przejścia.
Do wyższego stanu oscylacyjnego ν = 1 i stanu rotacyjnego ℓ + 1 o końcowej energii
3
𝐸ℓ+1 = 2 𝑓 + ℓ + 1 ℓ + 2 𝐸0𝑟
Do wyższego oscylacyjnego ν = 1stanu rotacyjnego scharakteryzowanego liczbą kwantową ℓ − 1 o
energii końcowej
3
𝐸ℓ−1 = 2 𝑓 + ℓ − 1 ℓ𝐸0𝑟
31.17
Różnice tych energii są równe:
∆𝐸ℓ→ℓ+1 = 𝐸ℓ+1 − 𝐸ℓ = 𝑓 + 2 ℓ + 1 𝐸0𝑟
31.18
gdzie ℓ = 0, 1, 2, … i
∆𝐸ℓ→ℓ−1 = 𝐸ℓ−1 − 𝐸ℓ = 𝑓 − 2ℓ𝐸0𝑟
31.19
gdzie ℓ = 1, 2, 3, …(W równaniu 31.19 ℓ zaczyna się od ℓ = 1 ponieważ z ℓ = 0 możliwe jest tylko
przejście ℓ → ℓ + 1). Rysunek 31.10 pokazuje te przejścia. Częstości odpowiadające tym przejściom
są określone przez
𝑓ℓ→ℓ+1 =
i
∆𝐸ℓ→ℓ+1
=𝑓+
2 ℓ+1 𝐸0𝑟
,
ℓ = 0, 1, 2, …
31.20
Wykład z fizyki – Piotr Posmykiewicz
𝑓ℓ→ℓ−1 =
Częstości
13
∆𝐸ℓ→ℓ−1
odpowiadające
=𝑓−
2ℓ𝐸0𝑟
,
ℓ = 1, 2, 3, …
31.21
przejściom
ℓ → ℓ + 1 są w związku z tym następujące: f +
2(E0r/h), f + 4(E0r/h), f + 6(E0r/h), itd., częstości
odpowiadające przejściom ℓ → ℓ − 1 są równe f
- 2(E0r/h), f - 4(E0r/h), f - 6(E0r/h), itd. W
rezultacie
absorpcyjne
możemy
będzie
oczekiwać,
zawierać
że
widmo
do
do
do
równomiernie
do
do
do
Rysunek 31.11
oddalone od siebie o 2E0r/h, oprócz przerwy
4E0r/h dla częstości oscylacyjnej f jak to jest pokazane na rysunku 31.11. Pomiar położenia przerwy
daje nam wartość f, a pomiar odległości pików absorpcyjnych daje wartośćE0r, która jest odwrotnie
proporcjonalna do momentu bezwładności cząsteczki.
Częstotliwość, Hz
Rysunek 31.12
Rysunek 31.12 przedstawia widmo absorpcyjne HCl. Podwójne wierzchołki na wykresie biorą się
stąd, że chlor naturalnie występuje w postaci dwu izotopów
35
Cl i
37
Cl, które posiadają różne
momenty bezwładności. Gdyby wszystkie poziomy na początku były zajęte równo, to należałoby
oczekiwać, że intensywność wszystkich linii absorpcyjnych powinna być jednakowa. Jednak
zapełnienie poziomów rotacyjnych ℓ jest proporcjonalne do zdegenerowania poziomu, to znaczy do
ilości stanów posiadających tę samą liczbę ℓ, których jest 2ℓ + 1 i do czynnika Boltzmanna 𝑒 −𝐸/𝑘𝑇 ,
gdzie E jest energią stanu. Dla małych wartości ℓ zapełnienie zwiększa się lekko, z powodu
czynnika zdegenerowania, podczas gdy dla większych ℓ zmniejsza się z powodu małej wartości
czynnika Boltzmanna ℓ. W związku z tym natężenie linii absorpcyjnych zwiększa się wraz z ℓ dla
małych wartości ℓ i zmniejsza się wraz ℓ dla dużych wartości ℓ, jak widać to na rysunku.
Wykład z fizyki – Piotr Posmykiewicz
14
31.3 Budowa ciał stałych.
Trzy fazy skupienia, które obserwujemy w przyrodzie wynikają z wzajemnej relacji między siłami
przyciągania między cząsteczkami, a energią cieplną cząsteczek. Cząsteczki znajdujące się w fazie
gazowej posiadają duże kinetyczne energie i nie oddziaływają na siebie, oprócz częstych ale
krótkich zderzeń. W odpowiednio niskich temperaturach (w zależności od typu wiązań)
odpowiedzialnymi za kondensowanie się gazów w ciecz, a potem w ciało stałe odpowiedzialne są
głównie siły van der Waalsa. W stanie ciekłym cząsteczki są dostatecznie blisko siebie, a ich energie
są dostatecznie niskie, aby tworzyć porządek krótkozasięgowy. W miarę jak energia kinetyczna
dalej maleje cząsteczki tworzą ciało stałe, w którym obserwuje się trwałe uporządkowanie.
Jeżeli ciecz jest ochładzana powoli, w ten sposób, że ich energia kinetyczna maleje powoli, wtedy
cząsteczki (lub atomy, lub jony) mogą organizować się tworząc uporządkowaną strukturę
krystaliczną, tworząc w ten sposób maksymalną ilość wiązań i zapewniając osiągnięcie minimum
energii potencjalnej układu krystalicznego. Jednak jeżeli układ jest ochładzany gwałtownie, tak, że
energia wewnętrzna jest usunięta szybciej niż cząsteczki zdążą ulec uporządkowaniu, wtedy ciało
stałe nie ma struktury krystalicznej, a przypomina raczej zdjęcie migawkowe cieczy. Takie ciała
stałe nazywamy amorficznymi. Wykazują one porządek krótkozasięgowy, a nie długozasięgowy
(rozciągający się na wiele cząsteczek), który jest charakterystyczny dla kryształów. Szkło jest
typowym
przykładem
ciała
amorficznego.
Charakterystyczną
cechą
uporządkowania
długozasięgowego kryształu jest to, iż posiada on dobrze określoną temperaturę topnienia, podczas
gdy amorficzne ciała stają się stopniowo coraz bardziej miękkie w miarę zwiększania temperatury.
Wiele materiałów przechodzi w stan stały tworząc stan amorficzny lub krystaliczny w zależności od
warunków zewnętrznych, inne przechodzą albo tylko w stan amorficzny, albo krystaliczny.
Większość typowych ciał stałych ma strukturę polikrystaliczną, co oznacza, że składają się one z
wielu pojedynczych kryształów, które łączą się na granicy ziaren. Zwykle kryształy mają rozmiary
rzędu ułamka milimetra. Jednak istnieją również duże kryształy
w przyrodzie lub są wytwarzane sztucznie. Najważniejszą cechą
pojedynczego kryształu (monokryształu) jest jego symetria i
powtarzalność jego budowy. Monokryształ możemy sobie
wyobrazić jako twór powstały z powielenia stałej jednostki
struktury. Ta najmniejsza jednostka strukturalna kryształu
nazywa się komórką elementarną.
Rysunek 31.13 przedstawia budowę kryształu jonowego NaCl.
Jony Na+ i Cl- mają symetrię sferyczną i jon chloru jest w
Rysunek 31.13
+
przybliżeniu dwukrotnie większy od jonu Na . Minimum energii
potencjalnej dla takiego kryształu pojawia się, gdy jon danego rodzaju ma sześciu najbliższych
Wykład z fizyki – Piotr Posmykiewicz
15
sąsiadów utworzonych z jonów drugiego rodzaju. Struktura taka nazywa się sześcienną płasko
centrowaną.
Wypadkowa energia potencjalna przyciągania się jonów w krysztale może być zapisana w postaci:
𝑈𝑝𝑟𝑧 = −𝛼
𝑘𝑒 2
31.22
𝑟
gdzie r jest odległością między sąsiednimi jonami (0,281nm w przypadku Na+ i Cl- w krysztale
NaCl), a α jest stałą Madelunga zależną od geometrii kryształu. Jeżeli liczy się tylko 6 najbliższych
sąsiadów, to α jest równe 6. Jednak uwzględniając dodatkowo 6 sąsiadów w postaci jonów mających
ładunek przeciwny znajdujących się w odległości r, mamy 12 jonów posiadających ten sam ładunek
w odległości
2r, 8 jonów o przeciwnym znaku w odległości
3r, itd. W związku z tym stała
Madelunga jest nieskończoną sumą:
∝= 6 −
12
+
2
8
3
− …
31.23
Dla struktury sześciennej płasko centrowanej α = 1,7476.
Kiedy jony Na+ i Cl- znajdują się bardzo blisko siebie, wtedy odpychają się z powodu zachodzenia
na siebie elektronów i zakazu Pauliego, o czym była mowa wcześniej. Prostym wyrażeniem
doświadczalnym na energię potencjalną związanym z odpychaniem, które sprawdza się całkiem
dobrze w praktyce jest:
𝐴
𝑈𝑜𝑑𝑝 = 𝑟 𝑛
gdzie A i n są stałymi. Całkowita energia potencjalna jest zatem
𝑈 = −𝛼
𝑘𝑒 2
𝑟
𝐴
+ 𝑟𝑛
31.24
Położenie równowagi r =r0 znajdziemy, gdy przyrównamy F = -dU/dr do zera. Licząc pochodną i
podstawiając -dU/dr = 0 w r = r0 otrzymujemy:
𝐴=
𝛼𝑘 𝑒 2 𝑟0𝑛 −1
31.25
𝑛
Całkowitą energię potencjalną możemy zatem zapisać w postaci:
𝑈 = −𝛼
𝑘𝑒 2 𝑟0
𝑟0
𝑟
1 𝑟0 𝑛
−𝑛
𝑟
31.26
W r = r0 mamy
𝑈 𝑟0 = −𝛼
𝑘𝑒 2
𝑟0
1
1−𝑛
31.27
Jeżeli znamy położenie równowagi r0, to wartość n można znaleźć w przybliżeniu na podstawie
energii dysocjacji kryształu, która jest równa energii do rozdzielenia kryształu na atomy.
Przykład 2.
Oblicz położenie równowagi r0 dla NaCl na podstawie zmierzonej gęstości, która wynosi ρ =
2,16g/cm3.
Wykład z fizyki – Piotr Posmykiewicz
16
Analiza zadania. Załóżmy, że jon zajmuje objętość sześcianu o boku r0. Masa jednego mola NaCl
jest równa 58,4g. Jony zajmują objętość 2NAr03, gdzie NA jest liczbą Avogadra.
𝑚
𝑚
1. Gęstość dana jest wzorem:
𝜌=
2. Obliczmy:
𝑟03 = 2𝑁
3. Otrzymujemy r0:
𝑟0 = 2,82 ∙ 10−8 𝑐𝑚 = 0,282𝑛𝑚
Zmierzona
dysocjacji
𝑉
= 2𝑁
𝑚
wartość
wynosi
dla
770kJ/mol. Wiedząc, że
𝐴𝜌
3
𝐴 𝑟0
=2
58,4𝑔
6,02∙10 23
2,16𝑔/𝑐𝑚 3
= 2,25 ∙ 10−23 𝑐𝑚3
energii
NaCl
1eV =
1,602 ∙ 10 J i że jeden mol NaCl
-19
zawiera NA par jonów możemy
obliczyć
energię
dysocjacji
w
elektronowoltach na parę jonów.
Rysunek 31.14
Otrzymujemy, że energia ta wynosi
7,98eV. Podstawiając -7,98eV za U(r0), 0,282nm za r0 i 1,75 za α do równania 31.27 otrzymujemy n
= 9.35≈9.
Większość kryształów jonowych takich jak LiF, KF, KCl, KI, AgCl ma strukturę sześcienną
płasko centrowaną. Taką samą budowę mają kryształy pierwiastków srebra, aluminium, złota,
wapnia, miedzi, niklu i ołowiu.
Rysunek 31.14 przedstawia strukturę CsCl zwaną sześcienną przestrzennie centrowaną. W tym
przypadku każdy atom ma 8 najbliższych sąsiadów w postaci jonów o przeciwnym ładunku. Stała
Madelunga, w tym wypadku, wynosi 1,7627. Taką samą strukturę posiadają: bar, cez, żelazo, potas,
lit, molibden i sód.
Rysunek 31.15 przedstawia inną ważną strukturę krystaliczną:
heksagonalną gęstego upakowania. Otrzymuje się ją poprzez
układanie jednakowych sfer, takich jak np. kule bilardowe. W
pierwszej warstwie każda kula styka się z sześcioma sąsiadami stąd nazwa. W następnej warstwie każda kula pasuje do
trójkątnego zagłębienia w pierwszej warstwie. W następnej
warstwie każda kula pasuje do zagłębienia w drugiej warstwie i
tym samym, leży dokładnie nad kulą w pierwszej warstwie. Taką
strukturę posiadają między innymi kryształy berylu, kadmu,
magnezu i cynku.
Rysunek 31.15
Wykład z fizyki – Piotr Posmykiewicz
17
W niektórych kryształach z wiązaniami kowalentnymi struktura jest zdeterminowana
bezpośrednio samą naturą wiązań. Rysunek 31.16 przedstawia strukturę diamentową węgla, w której
każdy atom jest połączony z czterema innymi atomami dzięki hybrydyzacji, o której była mowa w
części 31.2.
31.4 Półprzewodniki.
W części 28.4 była mowa, że niektóre materiały, takie jak
krzem czy german zachowują się jak półprzewodniki samoistne z
powodu małej przerwy energetycznej między zapełnionym
pasmem walencyjnym, a pustym pasmem przewodnictwa.
Półprzewodnikowe własności takich materiałów powodują, że są
one przydatne do budowy składowych obwodów elektronicznych,
których opór może być kontrolowany poprzez przykładanie
zewnętrznego napięcia. Jednak większość tego rodzaju urządzeń
Rysunek 31.16
takich jak diody półprzewodnikowe lub tranzystory zbudowanych
jest na bazie półprzewodników
domieszkowych, które powstają
Dodatkowy elektron
Dodatkowy elektron
Puste pasmo
przewodzenia
poprzez kontrolowane dodanie
niewielkiej ilości domieszki do
Domieszkowe
poziomy
donorowe
półprzewodnika
domieszkowego.
Proces
ten
nazywa się domieszkowaniem.
Rysunek
31.17a
przedstawia
schematycznie
domieszkowany
Pełne pasmo walencyjne
Rysunek 31.17
krzem
małą
ilością
arsenu, tak że niewielka ilość atomów arsenu zastępuje atomy krzemu w siatce krystalicznej. Arsen
posiada pięć elektronów walencyjnych w porównaniu z czterema elektronami walencyjnymi w
krzemie. Cztery z tych elektronów biorą udział w wiązaniu z czterema najbliższymi atomami
krzemu, a piąty elektron jest bardzo słabo związany z atomem. Ten dodatkowy elektron zajmuje
poziom energii, który jest położony tylko trochę poniżej pasma przewodzenia i łatwo może zostać
wzbudzony do pasma przewodnictwa, gdzie będzie uczestniczył w przewodnictwie elektrycznym.
Struktura pasmowa kryształu germanu z poziomami arsenu przedstawiona jest na rysunku 31.17b.
Poziomy widoczne tuż pod pasmem przewodnictwa są poziomami powstałymi dzięki
domieszkowaniu atomami arsenu. Te poziomy nazywają się poziomami donorowymi, ponieważ
dostarczają one elektrony do pasma przewodnictwa bez pozostawiania dziur w paśmie walencyjnym.
Wykład z fizyki – Piotr Posmykiewicz
18
Przewodnik taki nazywa się przewodnikiem typu n, ponieważ nośnikiem większościowym są
ujemne elektrony. Przewodnictwo domieszkowanych półprzewodników można kontrolować poprzez
domieszkowanie ich różną ilością dodawanej domieszki. Dodanie jednej części na milion zwiększa
przewodność
o
kilka
rzędów
Puste pasmo
przewodnictwa
wielkości.
Innym
typem
półprzewodnika
domieszkowego jest taki, w którym
Domieszkowe
poziomy
akceptorowe
Dziura
atom krzemu jest zamieniany na
Dziura
atom galu z trzema elektronami
walencyjnymi
(Rysunek
Atomy galu przyłączając elektrony z
pasma
walencyjnego
Pełne pasmo walencyjne
31.18a).
Rysunek 31.18
kompletują
swoje czteroatomowe wiązanie kowalencyjne i wytwarzają tym samym dziurę w paśmie
walencyjnym. Powstającą sytuację ilustruje rysunek 31.18b. Puste poziomy widoczne tuż nad
pasmem walencyjnym istnieją z powodu dziur w zjonizowanych atomach galu. Poziomy te
nazywają się poziomami akceptorowymi, ponieważ przyjmują one elektrony z wypełnionego pasma
walencyjnego, kiedy te elektrony są wzbudzane termicznie do wyższych stanów energetycznych. To
powoduje wytworzenie dziur w paśmie walencyjnym, które mogą się przemieszczać w kierunku
przyłożonego zewnętrznego pola. Takie półprzewodniki nazywają się półprzewodnikami typu p,
ponieważ nośnikami ładunku są dodatnie dziury.
31.5 Złącza półprzewodnikowe i urządzenia.
W urządzeniach półprzewodnikowych takich jak
diody i
Elektrony
Dziury
tranzystory stosuje się połączenia półprzewodników typu n i typu
p tak jak pokazane jest to na rysunku 31.19. W praktyce te dwa
typy półprzewodników są umieszczone w jeden kryształ krzemu
domieszkowany z jednej swojej strony domieszkami donorowymi
Strona p
i z drugiej domieszkami akceptorowymi. Obszar, w którym oba
Strona n
Rysunek 31.19
typy półprzewodników się łączą nazywamy złączem.
Energia
Kiedy półprzewodniki typu n i typu p zostaną doprowadzone do
kontaktu za sobą, wtedy z powodu niejednakowych koncentracji
elektronów i dziur następuje dyfuzja elektronów poprzez złącze z
Pasmo
przewodzenia
Pasmo
przewodzenia
części n do p i dziur z części p do n, aż do momentu ustalenia się
stanu równowagi. W wyniku tego następuje wypadkowe
przeniesienie ładunku dodatniego z p do n. Przeciwnie niż to ma
Pasmo
walencyjne
Pasmo
walencyjne
Złącze lub
warstwa
zubożona
Wykład z fizyki – Piotr Posmykiewicz
19
miejsce w przypadku dwu metali będących w kontakcie, elektrony nie mogą się przemieszczać
głęboko od obszaru złącza, ponieważ półprzewodnik nie jest dobrym przewodnikiem. Dlatego też ta
dyfuzja elektronów i dziur prowadzi do powstania podwójnej warstwy naładowanej podobnej do
naładowanego kondensatora. W rezultacie wytwarza się na złączu różnica potencjałów V, która stara
się zahamować dalszą migrację. W stanie równowagi strona n z dodatnim wypadkowym ładunkiem
będzie miała wyższy potencjał niż strona p z wypadkowym ujemnym ładunkiem. W obszarze złącza,
między naładowanymi warstwami znajduje się bardzo mało nośników ładunków obu typów, co
powoduje, że obszar złącza ma duży opór. Rysunek 31.20 przedstawia diagram pasmowy dla
połączenia p-n. Obszar ten nosi nazwę warstwy zubożonej (tj. praktycznie nieposiadającą
swobodnych nośników) lub warstwy zaporowej.
Prąd nie płynie
Diody.
Na
rysunku
31.21
przyłożona jest zewnętrzna
różnica
złącza
potencjałów
do
Polaryzacja w kierunku przewodzenia
p-n
poprzez
Rysunek 31.21
dołączenie ogniwa i oporu.
Kiedy
biegun
Polaryzacja w kierunku zaporowym
dodatni
ogniwa jest podłączony od strony p, jak pokazane
jest to na rysunku 31.21a, wtedy mówi się, że
złącze
jest
przewodzenia.
spolaryzowane
Spolaryzowanie
w
w
Polaryzacja
w kierunku
przewodzenia
kierunku
kierunku
Napięcie
przebicia
przewodzenia zmniejsza różnicę potencjałów na
złączu. W wyniku tego dyfuzja elektronów i dziur
zwiększa się, ponieważ na nowo starają się one
ustanowić stan równowagi, a to prowadzi do
Polaryzacja
zaporowa
przepływu prądu w obwodzie. Jeżeli biegun
dodatni ogniwa jest podłączony od strony n złącza,
jak pokazane jest to na rysunku 31.21b, wtedy
złącze
spolaryzowane
jest
w
Rysunek 31.22
kierunku
zaporowym. Spolaryzowanie w kierunku zaporowym stara się zwiększyć różnicę potencjałów na
złączu, a tym samym nie sprzyja dyfuzji. Rysunek 31.22 przedstawia wykres zależności prądu od
napięcia dla typowego złącza półprzewodnikowego. W zasadzie złącze przewodzi tylko w jednym
kierunku. Urządzenie z jednym złączem półprzewodnikowym nazywa się diodą. Diody posiadają
Wykład z fizyki – Piotr Posmykiewicz
20
szereg zastosowań. Jednym z nich jest zamiana prądu zmiennego na prąd stały. Proces ten nazywa
się prostowaniem.
Zwróćmy uwagę, że prąd na rysunku 31.22 ulega gwałtownemu wzrostowi w przypadku dużych
napięć w kierunku zaporowym. Dla tak dużych pól elektrycznych są wyrwane ze swoich wiązań i
ulegają przyspieszeniu przedostając się przez złącze. Z kolei elektrony te powodują zerwanie
następnych. Zjawisko takie nazywa się przebiciem lawinowym. Oczywiście takie przebicie może
być katastrofalne dla obwodu, tym niemniej jeżeli występuje ono w ściśle określonym zakresie
napięć jest pożyteczne, a dioda z taką charakterystyką nazywa się diodą Zenera.
Interesujące zjawisko, które omówimy tylko jakościowo, ma miejsce, jeżeli obie strony n i p
Pasmo
przewodnictwa
Pasmo
przewodnictwa
Pasmo
przewodnictwa
Tunelowanie
Puste
Pełne
Pasmo
walencyjne
Pasmo
walencyjne
Pasmo
walencyjne
Rysunek 31.23
złącza p-n diody są silnie domieszkowane. Takie domieszkowanie powoduje, że donory po stronie n
złącza dostarczają tak dużo elektronów, że niższe partie pasma przewodnictwa są praktycznie
całkowicie zapełnione, a akceptory po stronie p przyjmują tak dużo elektronów, że górne rejony
pasma walencyjnego są prawie puste. Rysunek 31.23a przedstawia diagram poziomów
energetycznych w opisanej sytuacji. Ponieważ warstwa zaporowa jest teraz bardzo wąska, to
elektrony mogą łatwo wnikać w barierę potencjału na granicy złącza i przedostawać się, dzięki
efektowi tunelowemu na drugą stronę. Przepływ przez barierę nazywa się prądem tunelowym, a
tego rodzaju diody silnie domieszkowane nazywają się diodami tunelowymi. W stanie równowagi,
przy braku zewnętrznej polaryzacji płynie jednakowy prąd w obu kierunkach. Kidy zostaje
przyłożone niewielkie napięcie w kierunku przewodzenia diagram poziomów energii wygląda jak na
rysunku 31.23b i ulega zwiększeniu tunelowanie elektronów ze strony n do p, podczas gdy w
kierunku przeciwnym ulega ono zmniejszeniu. Prąd tunelowania razem ze zwykłym prądem
spowodowanym dyfuzją daje w rezultacie znaczny prąd wypadkowy. Kiedy zwiększyć lekko
napięcie, wtedy diagram energii wygląda jak na rysunku 31.23c i prąd tunelowy ulega zmniejszeniu.
Mimo, iż prąd dyfuzyjny ulega zwiększeniu, to prąd wypadkowy ulega zmniejszeniu. Przy dużych
napięciach prąd tunelowy może być całkowicie pominięty i prąd całkowity zwiększa się wraz ze
wzrostem napięcia polaryzującego z powodu wzrostu prądu dyfuzyjnego jak to ma miejsce w
zwykłym złączu p-n diody. Rysunek 31.24 pokazuje zależność natężenia prądu od napięcia dla
Wykład z fizyki – Piotr Posmykiewicz
21
diody tunelowej. Diody tego rodzaju używane są w obwodach
elektrycznych posiadają bardzo krótki czas reakcji. Jeżeli
dioda działa w okolicach wierzchołka A na wykresie, wtedy
mała zmiana napięcia polaryzującego spowoduje duże zmiany
natężenia prądu.
Innym rodzajem zastosowania półprzewodnikowego złącza
p-n jest ogniwo słoneczne przedstawione schematycznie na
rysunku 31.25. Kiedy foton o energii większej niż przerwa
rysunku 31.24
energetyczna (w krzemie - 1,1eV) uderza obszar typu p, to
może
spowodować
wzbudzenie
elektronu
z
pasma
Padające światło
walencyjnego do pasma przewodzenia, pozostawiając dziurę
w paśmie walencyjnym. Ten obszar jest już bogaty w dziury.
Niektóre
elektrony
wytworzone
przez
fotony
będą
Typ p
Typ n
rekombinować z dziurami, ale część z nich będzie migrować
w kierunku złącza. Stamtąd będą przyspieszane do obszaru
rysunku 31.25
typu n przez pole elektryczne między warstwą podwójną
ładunków. To spowoduje nadwyżkę ładunku ujemnego w obszarze typu n i nadmiar ładunku
dodatniego w obszarze typu p. W rezultacie wytworzy się różnica potencjałów, która w praktyce
wynosi około 0,6V. Jeżeli połączyć te dwa obszary opornikiem obciążeniowym, wtedy popłynie
prąd przez opornik. W ten sposób energia słoneczna jest zamieniana w energię elektryczną.
Natężenie prądu płynącego przez opór jest proporcjonalne do ilości padających fotonów, a to jest z
kolei proporcjonalne do natężenia padającego światła.
Istnieje cały szereg zastosowań złącz p-n. Detektor cząstek zwany detektorem z powierzchniową
barierą składa się ze złącza p-n spolaryzowanego silnie w kierunku zaporowym, tak że normalnie
nie płynie przez nie prąd. Kiedy cząsteczka wysoko energetyczna cząstka, taka jak elektron,
przechodzi przez półprzewodnik, to wywołuje powstanie szeregu par elektron – dziura, a sama traci
energię. Powstający w wyniku tego impuls prądowy sygnalizuje przejście cząstki. Diody LED
(Light-emitting diode) są półprzewodnikowymi złączami typu p-n, które są silnie spolaryzowane w
kierunku przewodzenia. Taka polaryzacja prowadzi do wytworzenia dużej nadmiarowej koncentracji
elektronów w części p i dziur w części n złącza. W takich warunkach dioda emituje światło, gdy
dziury i elektrony ulegają rekombinacji. W istocie rzeczy jest to proces odwrotny do tego, jaki
powstaje w ogniwie słonecznym, w którym pod wpływem światła tworzą się pary elektron – dziura.
Diody LED są powszechnie używane w wszelkiego rodzajach wskaźnikach świetlnych.
Tranzystory.
Wykład z fizyki – Piotr Posmykiewicz
22
Tranzystor jest urządzeniem półprzewodnikowym,
które jest stosowane w celu wytworzenia żądanego
sygnału wyjściowego w odpowiedzi na sygnał
wejściowy. Tranzystor został wynaleziony w 1948
Kolektor
Typ p
Kolektor
Baza
Typ n
Emiter
Typ p
Baza
Emiter
roku przez Shockleya, Bardeena i Brataina co
doprowadziło do zrewolucjonizowania przemysłu
elektronicznego i naszego codziennego życia. Prosty
tranzystor ze złączem bipolarnym składa się z trzech
wyodrębnionych
obszarów
rysunku 31.26
półprzewodnikowych
zwanych emiterem, bazą i kolektorem. Baza jest
bardzo
cienkim
obszarem
jednego
z
typów
półprzewodników umiejscowiona między dwoma
obszarami
przeciwnego
Półprzewodnikowy
domieszkowany
tranzystorze
emiter
niż
npn,
półprzewodnikami
typu
półprzewodników.
jest
znacznie
czy
kolektor.
W
emiter
i
kolektor
są
baza
jest
n,
a
Typ n
Baza
Typ p
silniej
baza,
typu
Kolektor
Kolektor
Baza
Emiter
Emiter
Typ n
półprzewodnikiem typu p. W tranzystorze pnp, emiter
i kolektor są półprzewodnikami typu p, a baza jest
rysunku 31.27
półprzewodnikiem typu n.
Rysunek 31.26 i rysunek 31.27 przestawiają tranzystory pnp i
npn wraz z symbolami, które reprezentują te typy tranzystorów w
obwodach elektrycznych. Widzimy, że każdy z tranzystorów składa
Typ p
Typ n
się z dwu złączy p-n. Przedyskutujemy zasadę działania tranzystora
Typ p
pnp. Działanie tranzystora npn jest podobne.
W typowej pracy złącze emiter – baza jest spolaryzowane w
kierunku przewodzenia, a baza – kolektor w kierunku zaporowym
rysunku 31.28
jak jest pokazane na rysunku 31.28. Silnie domieszkowany emiter typu p wytwarza dziury, które
przepływają przez złącze emiter – baza do bazy. Ponieważ baza jest cienka, większość z tych dziur
przepływa przez bazę do kolektora. Ten przepływ tworzy prąd Ic z emitera do bazy. Jednak niektóre
dziury rekombinują w bazie wytwarzając dodatni ładunek, który hamuje dalszy przepływ prądu. Aby
zapobiec temu, dziury które nie dotarły do kolektora są odprowadzane z bazy w postaci prądu bazy
Ib do obwodu połączonego z bazą. Dlatego też, na rysunku 31.28 prąd Ic jest prawie, ale nie
całkowicie równy prądowi Ie, a prąd Ib jest znacznie mniejszy zarówno od Ic jak i od Ie. Zwykle Ic
zapisuje się jako:
Wykład z fizyki – Piotr Posmykiewicz
23
𝐈𝐜 = 𝛃𝐈𝐛
31.28
gdzie β nazywa się współczynnikiem wzmocnienia tranzystora. Projektuje się tranzystory, które
mają współczynniki wzmocnienia od 10 do kilkuset.
Rysunek
31.29
przedstawia
prosty tranzystor pnp użyty jako
wzmacniacz. Małe, zmienne w
czasie
νS
napięcie
Wyjści
e
wejściowe
włączone jest w szereg z napięciem
polaryzującym bazę Veb. Prąd bazy
jest zatem sumą prądu stałego Ib
Wejści
e
wytworzonego przez napięcie bazy
Veb
i
prądu
zmiennego
ib
rysunku 31.29
powstałego z powodu napięcia sygnału νS. Ponieważ νS może być w dowolnej chwili dodatnie lub
ujemne, to napięcie Veb musi być na tyle duże, aby zapewnić przez cały czas spolaryzowanie złącza
emiter – baza w kierunku przewodzenia. Prąd kolektora składa się z dwu części: prądu stałego Ic =
βIb i prądu zmiennego ic = βib. W ten sposób otrzymujemy wzmacniacz, w którym zmienny prąd
wyjściowy ic jest β razy większy od zmiennego prądu wejściowego ib. Dla tego typu wzmacniaczach
stałe prądy Ic i Ib mimo, iż istotne z punktu widzenia działania tranzystora, nie mają znaczenia.
Napięcie wejściowe sygnału związane jest z prądem bazy poprzez prawo Ohma:
𝑖𝑏 = 𝑅
𝜈𝑆
31.29
𝑏 +𝑟 𝑏
gdzie rb oporem wewnętrznym tranzystora między bazą, emiterem. Podobnie prąd kolektora i c
wywołuje napięcie νL na wyjściu lub oporze obciążenia RL, co można zapisać:
𝜈𝐿 = 𝑖𝑐 𝑅𝐿
31.30
Stosując równanie 31.28 i 31.29 otrzymujemy:
𝑖𝑐 = 𝛽𝑖𝑏 = 𝛽 𝑅
𝜈𝑆
31.31
𝑏 +𝑟 𝑏
Napięcie wyjściowe związane jest z napięciem wejściowym poprzez równanie:
𝜈𝐿 = 𝛽 𝑅
𝑅𝐿
𝑏 +𝑟 𝑏
𝜈𝑆
31.32
Stosunek napięcia wyjściowego do napięcia wejściowego nazywa się wzmocnieniem napięciowym
wzmacniacza:
𝛎
𝐖𝐳𝐦𝐨𝐜𝐧𝐢𝐞𝐧𝐢𝐞 𝐧𝐚𝐩𝐢ę𝐜𝐢𝐨𝐰𝐞 = 𝛎𝐋 = 𝛃 𝐑
𝐒
𝐑𝐋
𝐛 +𝐫𝐛
31.33
Wykład z fizyki – Piotr Posmykiewicz
24
Typowy wzmacniacz, na przykład w odtwarzaczu, posiada kilka tranzystorów podobnych do tego z
rysunku 31.29, które są połączone w szereg w ten sposób, że wyjście z jednego tranzystora jest
jednocześnie wejście następnego. W ten sposób bardzo małe napięcie powstałe w wyniku przejścia
głowicy zbierającej obok określonego wycinka taśmy magnetycznej powoduje powstanie
wyjściowego sygnału o dużej mocy zdolnego do wzbudzenia głośnika. Moc dostarczana do głośnika
jest pobierana ze źródeł prądu stałego podłączonych do każdego tranzystora.
Technologia półprzewodników nie ogranicza się tylko do pojedynczych diod, czy tranzystorów.
Szereg urządzeń, które powszechnie używamy, takie jak komputery i elementy kierujące wszelkiego
rodzaju urządzeniami poczynając od samolotów, a kończąc na pralce, działają w oparciu o
zintegrowane układy (układy scalone) zawierające wiele tranzystorów i innych składników obwodu.
Współczesne układy scalone mogą zawierać setki milionów podstawowych elementów
elektronicznych, takich jak tranzystory, diody, rezystory, kondensatory.